Complete Solutions to Dynamics Of Circular Motion of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| A2Z | Dynamics Of Circular Motion |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
An unbanked curve has a radius of 60m. The maximum speed at which a car can make a turn if the coefficient of static friction is `0.75` , is
03:22View SolutionA person wants to drive on the vertical suirface of a large cylindrical wooden `well` commonly known as `death well` in a circus. The radius of the well 2 meter, and the coefficient of friction between the tyers of the motorcycle and the wall of the well is `0.2` the minimum speed the motorcyclist must have in order to prevent slipping should be
02:58View SolutionWater in a bucket is whirled in a vertical circle with a string attached to it. The water does not fill down even when the bucket is inverted at the top of its path. We conclude that in this position
04:05View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
01:42View SolutionA motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
03:30View SolutionThree identical cars A,B and C are moving at the same speed on three bridges. The car A goes on a plane bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let `F_A,F_B and F_C` be the normal forces exerted by the cars on the bridges when they are at the middle of bridges
03:56View SolutionA train A runs from east to west and another train B of the same maas runs from west to east at the same speed along the equator. A presses the track with a force `F_1 and B` presses the track with a force F.
07:30View SolutionA car turns a corner on a slippery road at a canstant speed of `12m//s` . If the co0efficient is `0.4` , the minimum radius of the arc in metres in which the car truns is.
02:40View SolutionA small objective placed on a rotating horizontal trun table just slip when it is placed at a distance 4cm from the axis of rotation. If the angular velocity of the trun-table doubled, the objective slip when its distance from the axis of ratation is.
05:14View SolutionAn automobile of mass `m` is crossing over a convex upward over bridge with a speed `v` . If the radius of the bridge is `r` the thrusrt on the bridge at the highest point will be.
01:55View SolutionA curved road of 50m in radius is banked to correct angle for a given speed. If the speed is to be double keeping the same banking angle, the radius of curvature of the road should be changed to.
04:18View SolutionA stone of mass `m` is tied to a strin and is moved in a vertical circle of radius `r` making `n` revolution per minute. The total tension in the string when the stone is its lowest point is.
04:22View SolutionA stone tied to a string is rotated with a uniform speed in a vertical plane. If mass of the stone is `m`, the length of the string is `r` and linear speed of the stone is `v` when the stone is at its lowest point, then the tension in the string will be
(g= acceleration due to gravity)01:41View SolutionThree identical particles are joined together by a thread as shown in figure All the partical are moving in a horizontal plane If the vertical of the outermost particle is `v_(0)` then the ratio of tension in the three sections of the string `(T_(1):T_(2):T_(3) = ?)` is
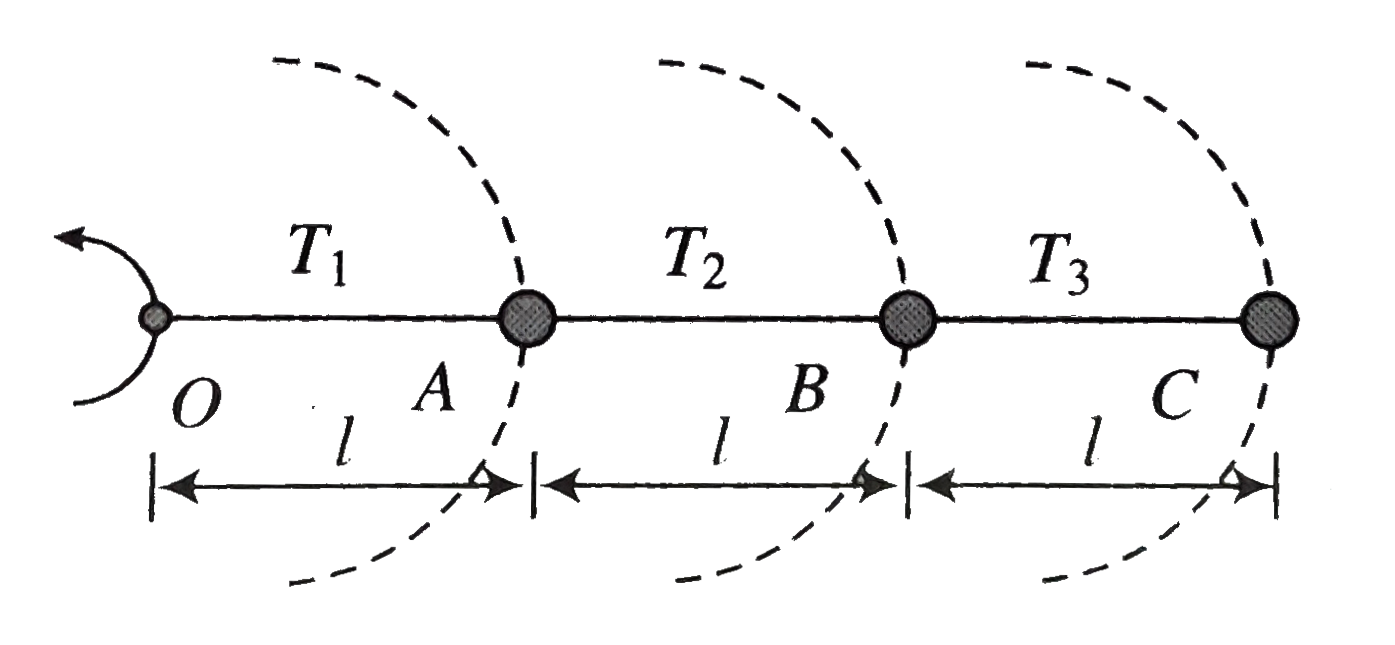 02:45View Solution
02:45View SolutionA block of mass `M` is situation on a smooth horizontal frictionless table. A thread tied to the block passes through a hole in the table and carries a mass `m` at its other end if the length of the thread above the table is l, what should be the value of `m` so that it may remain suspended at a constant height and the block `M` moves in a circular p-ath with an angular velocity `omega` on the table?
 03:08View Solution
03:08View SolutionA string of length `l=1m` is fixed at one end carries a mass of 100gm at other end. The string makes `sqrt(5)//(pi)` revolutions per second about a verticle axis passing through its second end. What is the angle of inclination of the string with the vertical?
06:53View SolutionA stone of mass 1kg tied to a light inextensible sstring of length `L=10m` is whirling in a circular path of radius `L` in vertical plane. If the ratio of the maximum tension in the string to the minimmum tension in the string is 4 and if `g` is taken to be `10ms^(-2)` , the speed of the stone at the highest point of the circle is.
11:39View SolutionA 8kg stone tied at the end of a string 1 metre long is whirled in a vertical circle. At the instant when the string makes an angle theta with the vertical, the speed of the stone is `4ms^(-1)` and the tension in the thread is 104N. Then theta is.
04:04View Solutiona truck is carry a box of mass `m=50kg` on its flat horizontal rough surface with coefficient of friction `mu=0.3` . It is crossing a circular track of radius 27m. What is the maximum speed of the truck so thet the box does not slide from the truck while moving on the circular path?
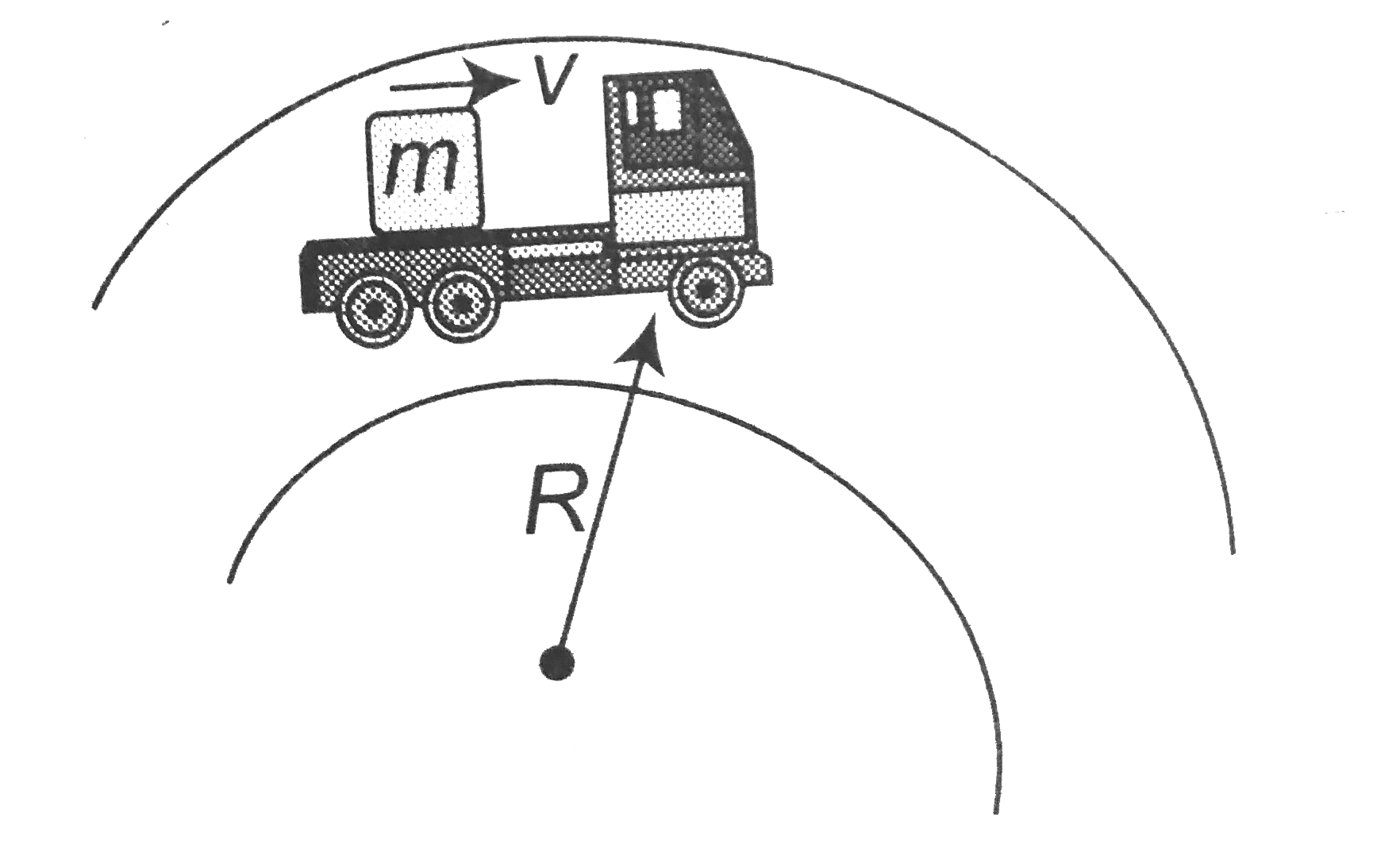 04:08View Solution
04:08View SolutionIndicate the direction of frictional force on a car which is moving along the curved path with non zero tangential acceleration, in anti-clock direction:
02:39View SolutionA partical of mass `m` is attached to a massless string of length `l` and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is `T=kmg` .
04:15View SolutionA pendulum of length `l=1m` is released from `theta_(0)=60^(@)` . The rate of change of speed of the bob at `theta=30^(@)` is.
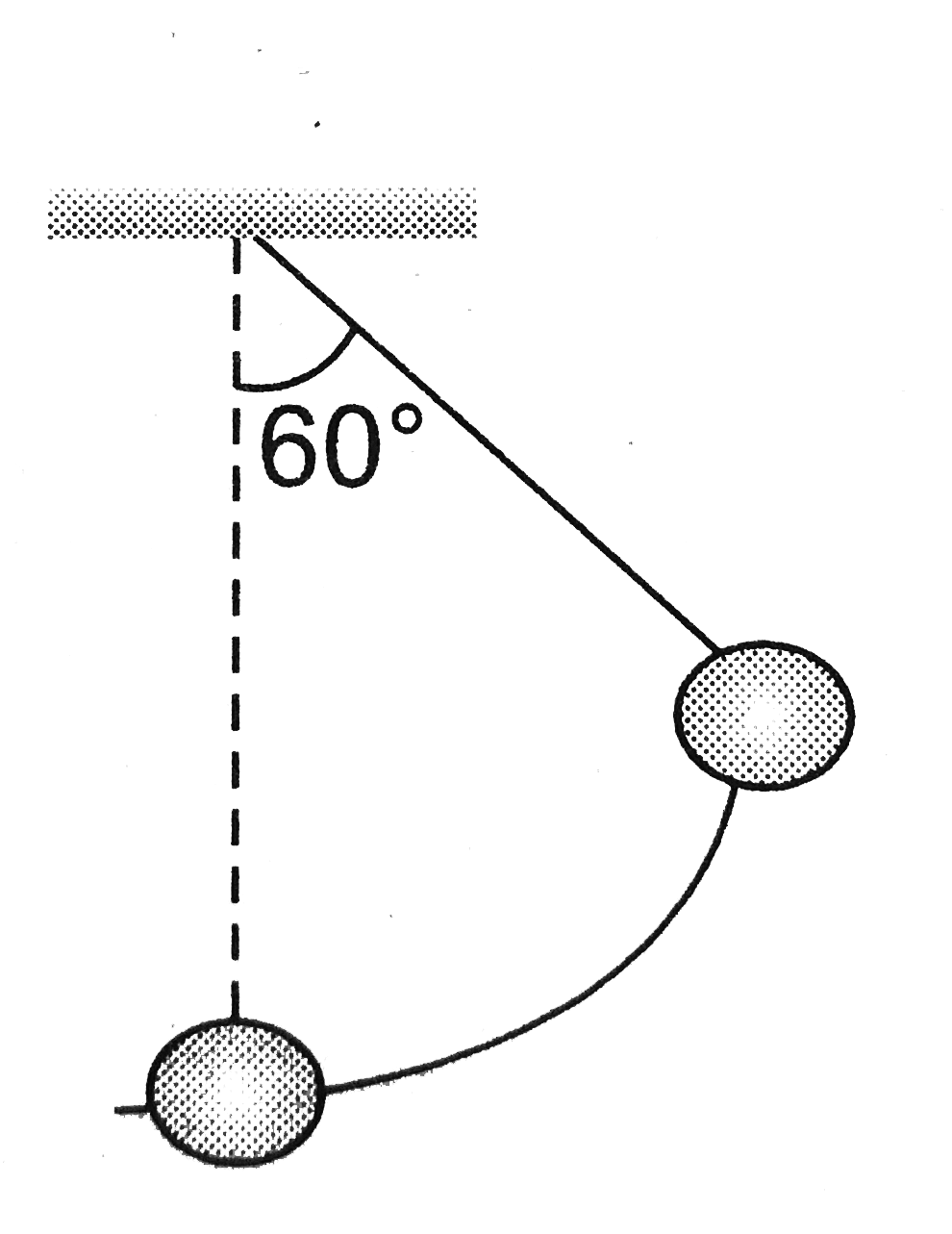 03:50View Solution
03:50View SolutionTwo partical tied to different strings are whirled in a horizontal circle as shown in figure. The ratio of lengths of the string so that they complete their circular path with equal time priod is:
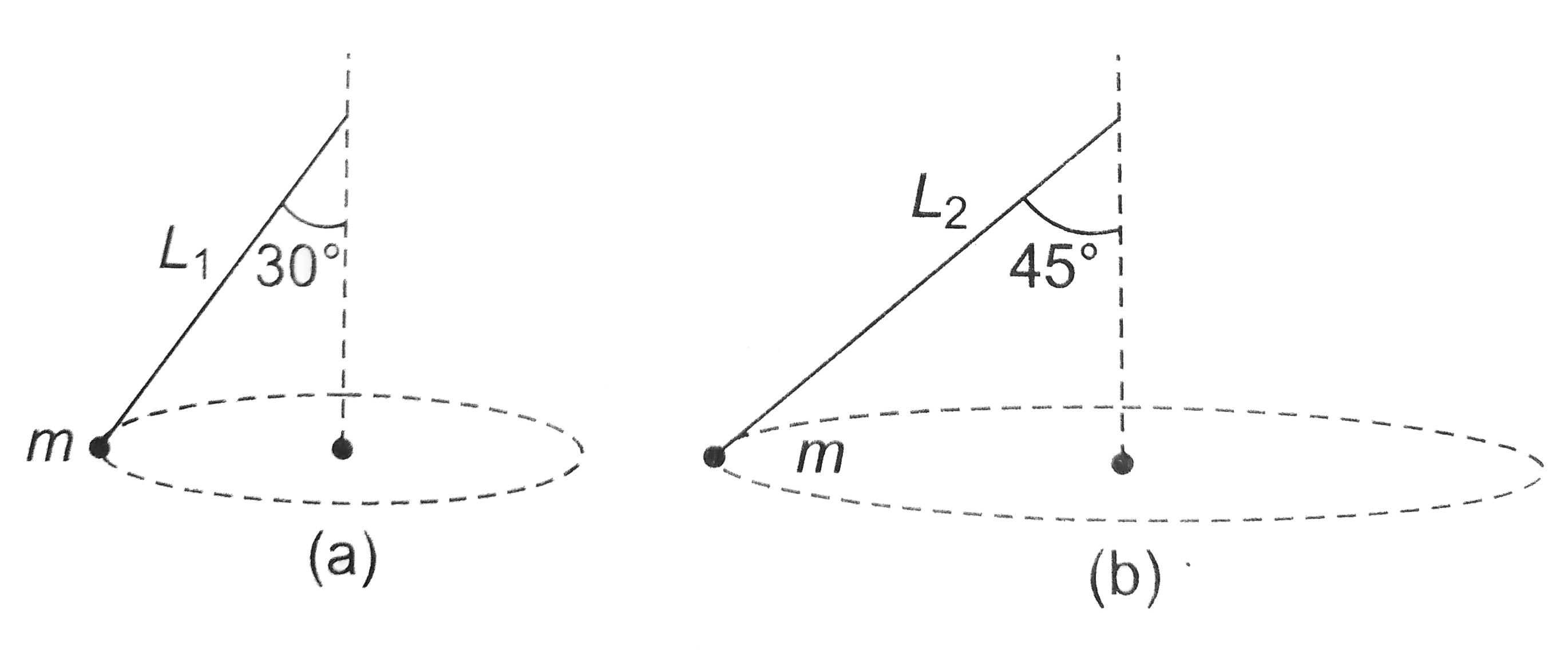 03:11View Solution
03:11View SolutionA smooth wire is bent into a vertical circle of radius a. `A` bead `P` can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead `P` is at rest w.r.t. the circular ring in the position shown. then `omega^(2)` is equal to:
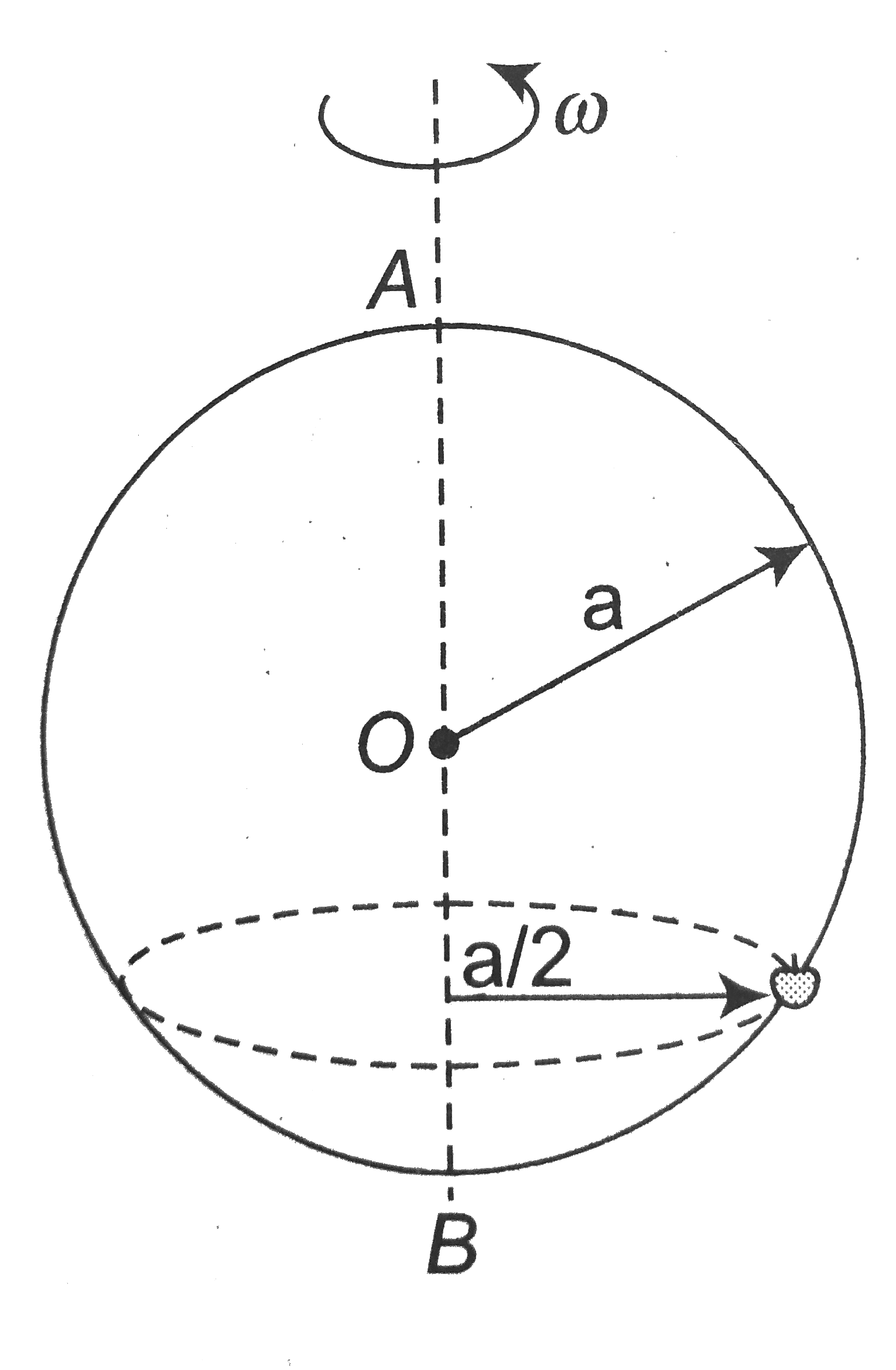 06:52View Solution
06:52View SolutionA particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is `m` . The force exerted by the rod on the particle is `vecF` , then:
02:12View SolutionThree masses of small size are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency `omega` (one such circle is drawn in the shown figure.) Then pick up the correct statement.
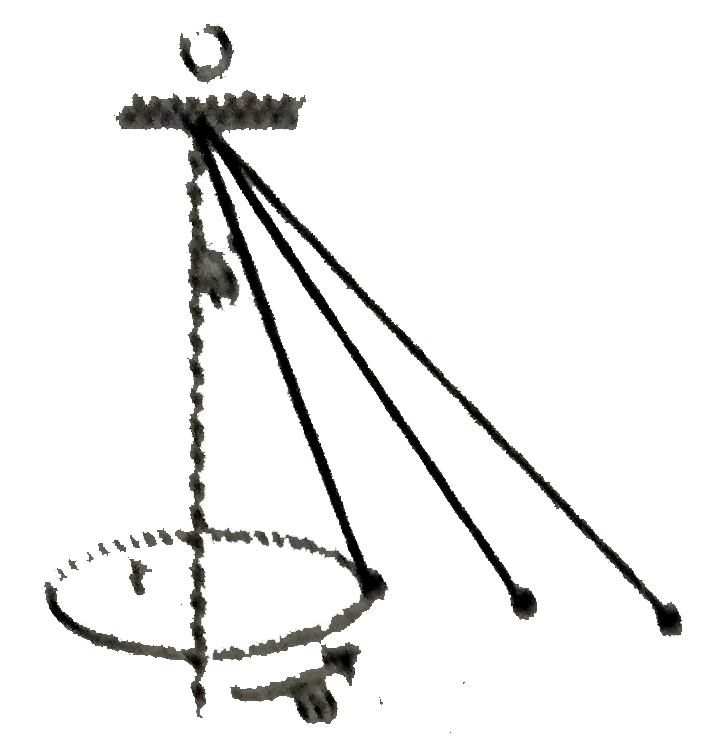 03:32View Solution
03:32View SolutionA bus is moving with a constant acceleration `a=3g//4` towards right. In the bus, a ball is tied with a rope and is rotated in vertical circle as shown. The tension in the rope will be minimum, when the rope makes an angle `theta=________`
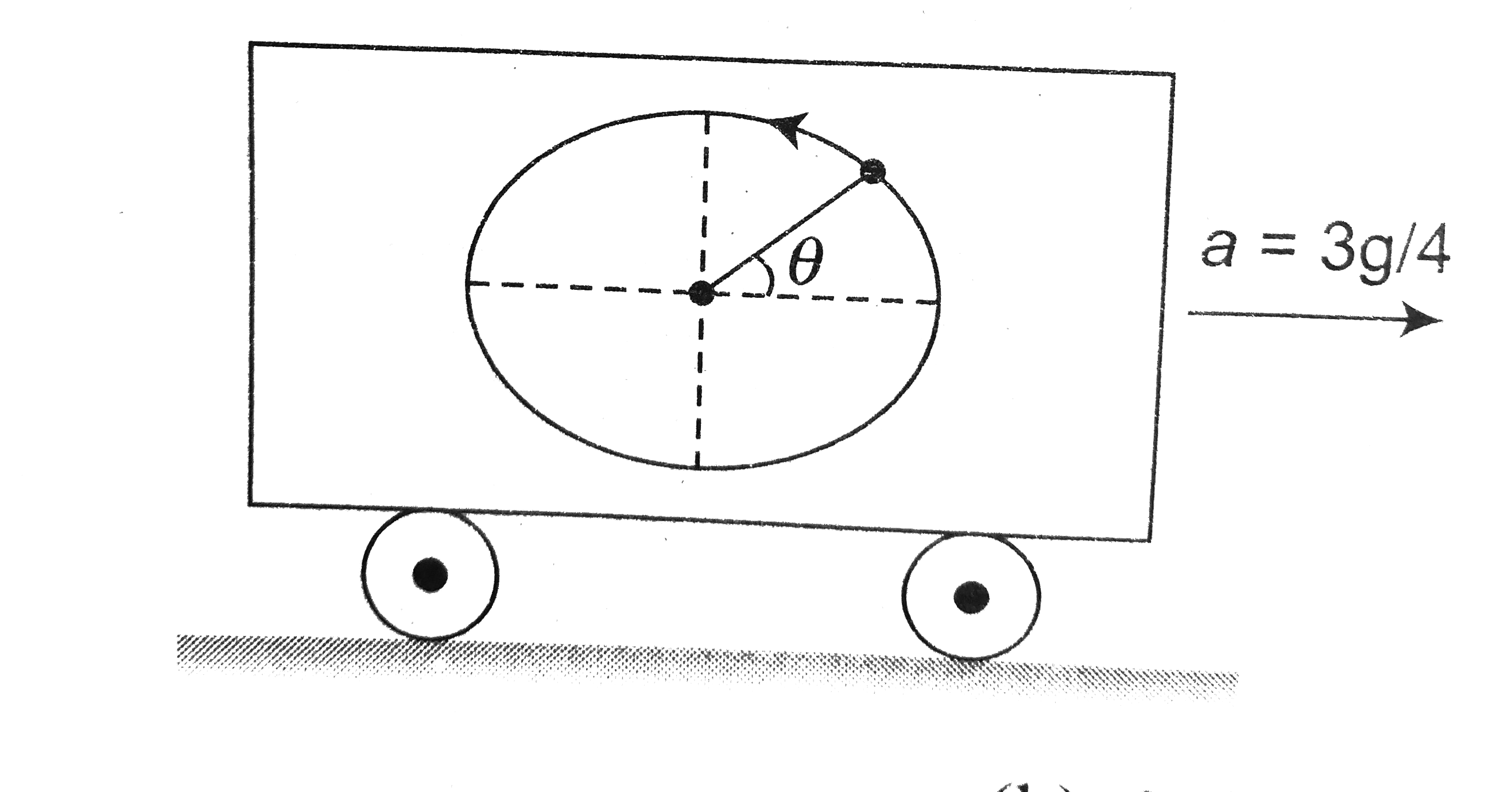 09:08View Solution
09:08View SolutionA small sized mass `m` is attached by a massless string (of length `L`) to the top of a fixed frictionless solid cone whose axis is vertical. The half angle at the vertex of cone is theta. If the mass `m` moves around in a horizontal circle at speed `v` , what is the maximum value of `v` for which mass stay in contact with the comes? (g is acceleration due to gravity.)
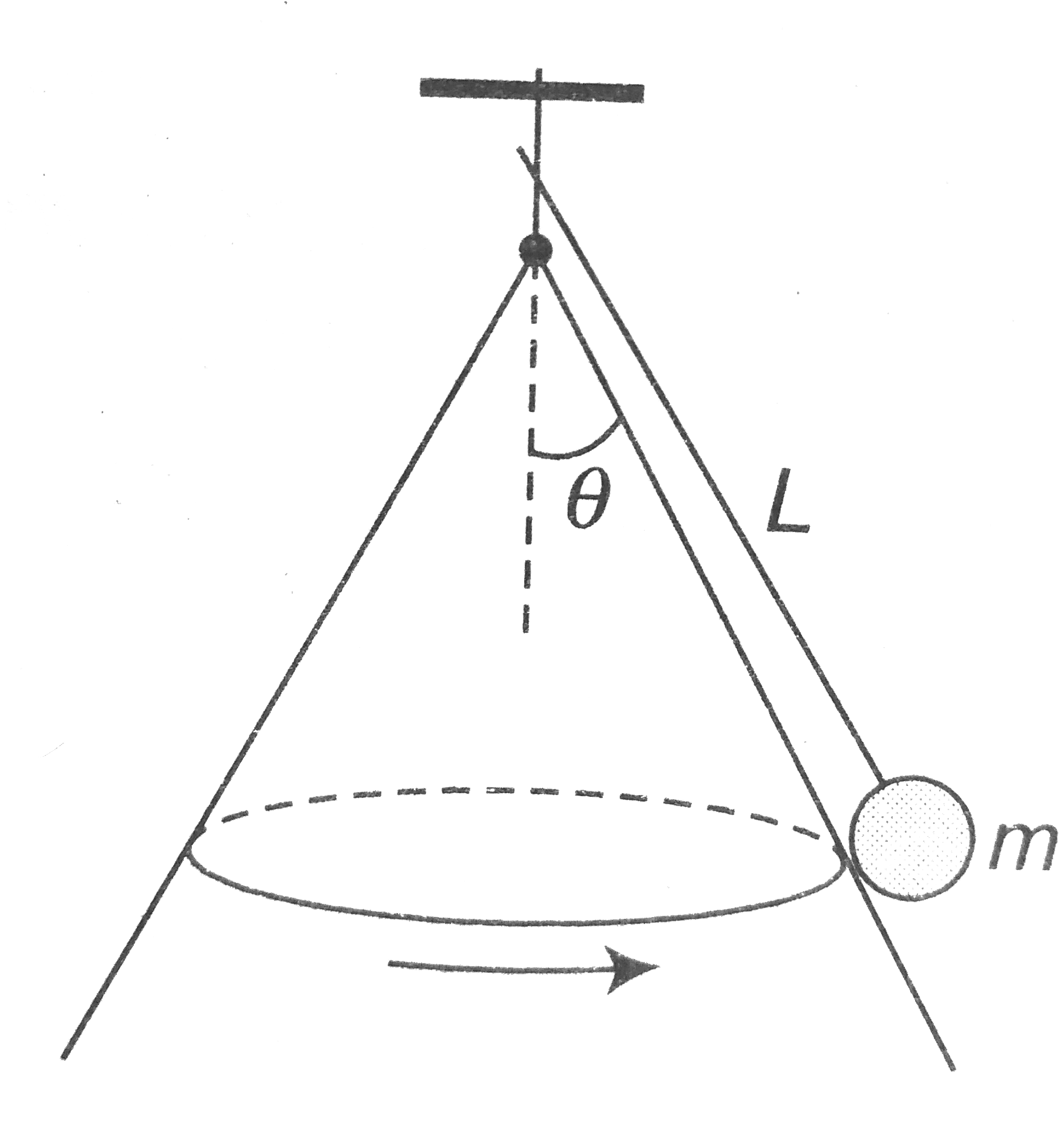 04:10View Solution
04:10View SolutionA small sized mass `m` is attached by a massless string (of length `L`) to the top of a fixed frictionless solid cone whose axis is vertical. The half angle at the vertex of cone is theta. If the mass `m` moves around in a horizontal circle at speed `v` , what is the maximum value of `v` for which mass stay in contact with the comes? (g is acceleration due to gravity.)
06:13View SolutionA particle describes a horizontal circle in a conical funnel whose inner surface is smooth with speed of `0.5m//s` . What is the height of the plane of circle from vertex the funnel?
04:30View SolutionA main revolves a stone of mass `m` tied to the end of a string in a circle of radius R The net force at the lowest and beight point of the circle directed vertical downward are
Here`T_(1),T_(2)` and `(v_(1),v_(2))` denote the tension in the string (and the speed of the stone) at the lowest and highest points, respectively.03:08View Solution
Dynamics Of Circular Motion questions and complete solutions for chapter NEWTONS LAWS OF MOTION of A2Z PHYSICS (HINGLISH) of Class 11
