Complete Solutions to Problems Based On Mixed Concepts of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| A2Z | Problems Based On Mixed Concepts |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
In the arrangement shown in figure the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed
 01:22View Solution
01:22View SolutionThree block 1, 2 and 3 are arranged as shown in the figure. The velocities of the blockes `v_(1)` , `v_(2)` and `v_(3)` are shown in the figure. What is the relationship between `v_(1)` , `v_(2)` and `v_(3)` ?
 03:33View Solution
03:33View SolutionFind velocity of ring `B` `(V_(B))` at the instant shown. The string is taut and inextensible:
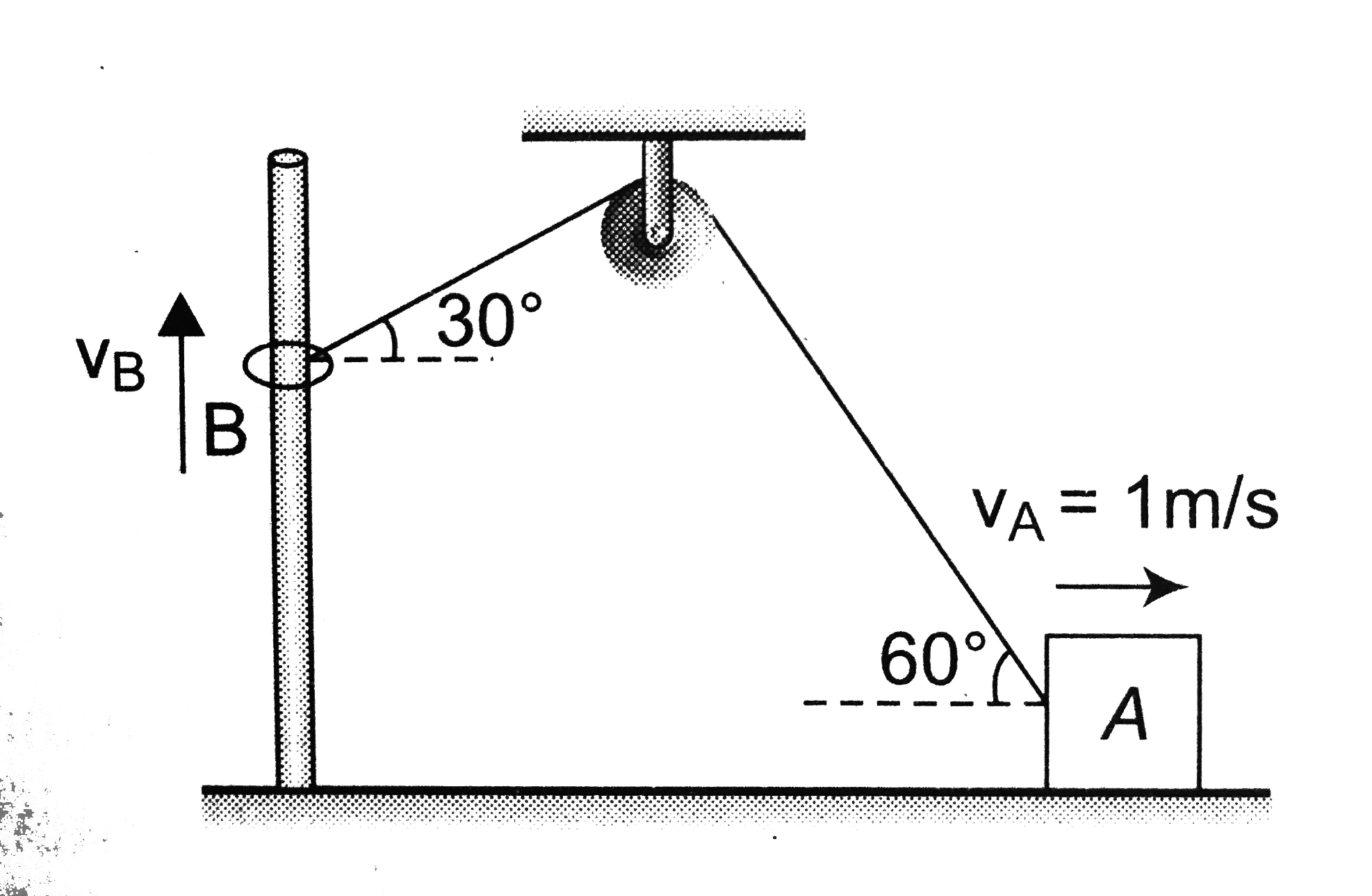 04:09View Solution
04:09View SolutionThe ratio of acceleration of pulley to the acceleration of the block is (string is inextensible).
 03:14View Solution
03:14View SolutionIn the arrangement shown, the pulleys and the string are ideal. The acceleration of block `B` is.
 05:38View Solution
05:38View SolutionIn each of the three arrangements, the block of mass `m_(1)` is being pulled left with constant velocity. There is no friction anywhere. The string are light and anextensible and pulleys are massless. The ratio of the speed of the block of mass `m_(2)` in the three cases respectively is:
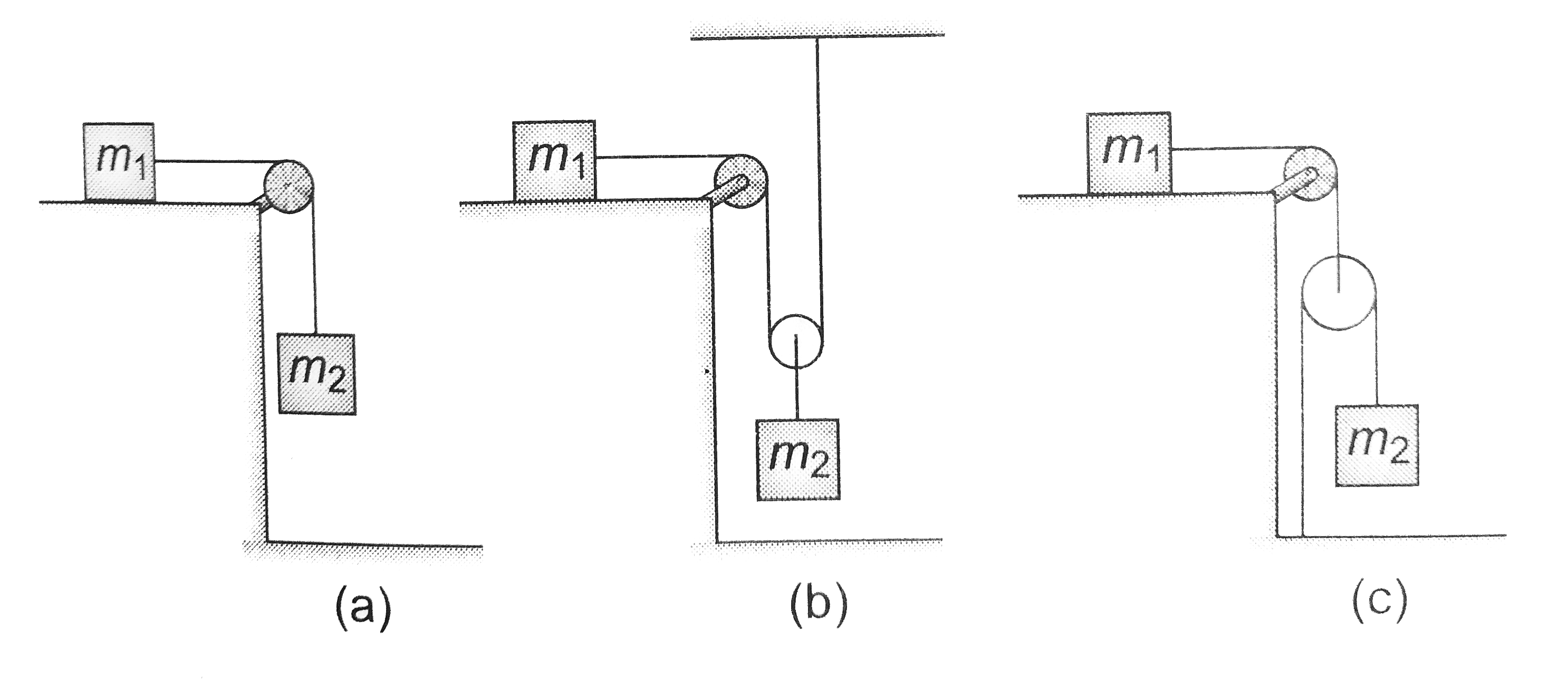 03:44View Solution
03:44View SolutionIf the blocks are moving as shown in the figure the relation between `a_(1)` , `a_(2)` and `a_(3)` will be.
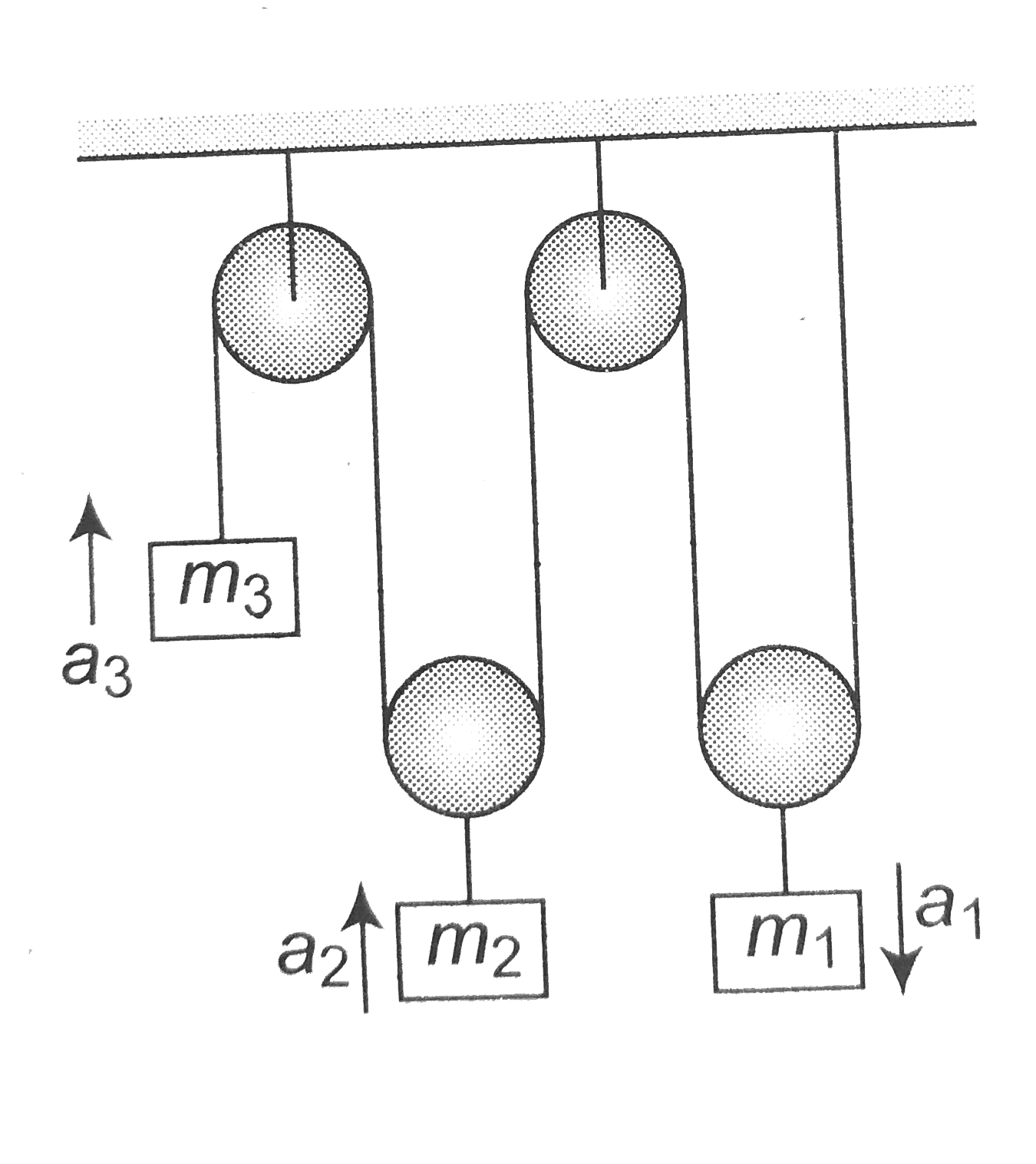 05:26View Solution
05:26View SolutionIn the figure acceleration of `A` is `1m//s^(2)` upward, acceleration of `B` is `7m//s^(2)` upward acceleration of `C` is `2m//s^(2)` upward. The acceleration of `D` will be.
 03:49View Solution
03:49View SolutionFor the pulley system shown in fig. each of the cables at A and B is given a velocity of `2ms^(-1)` in the direction of the arrow. Determine the upward velocity v of the load m.
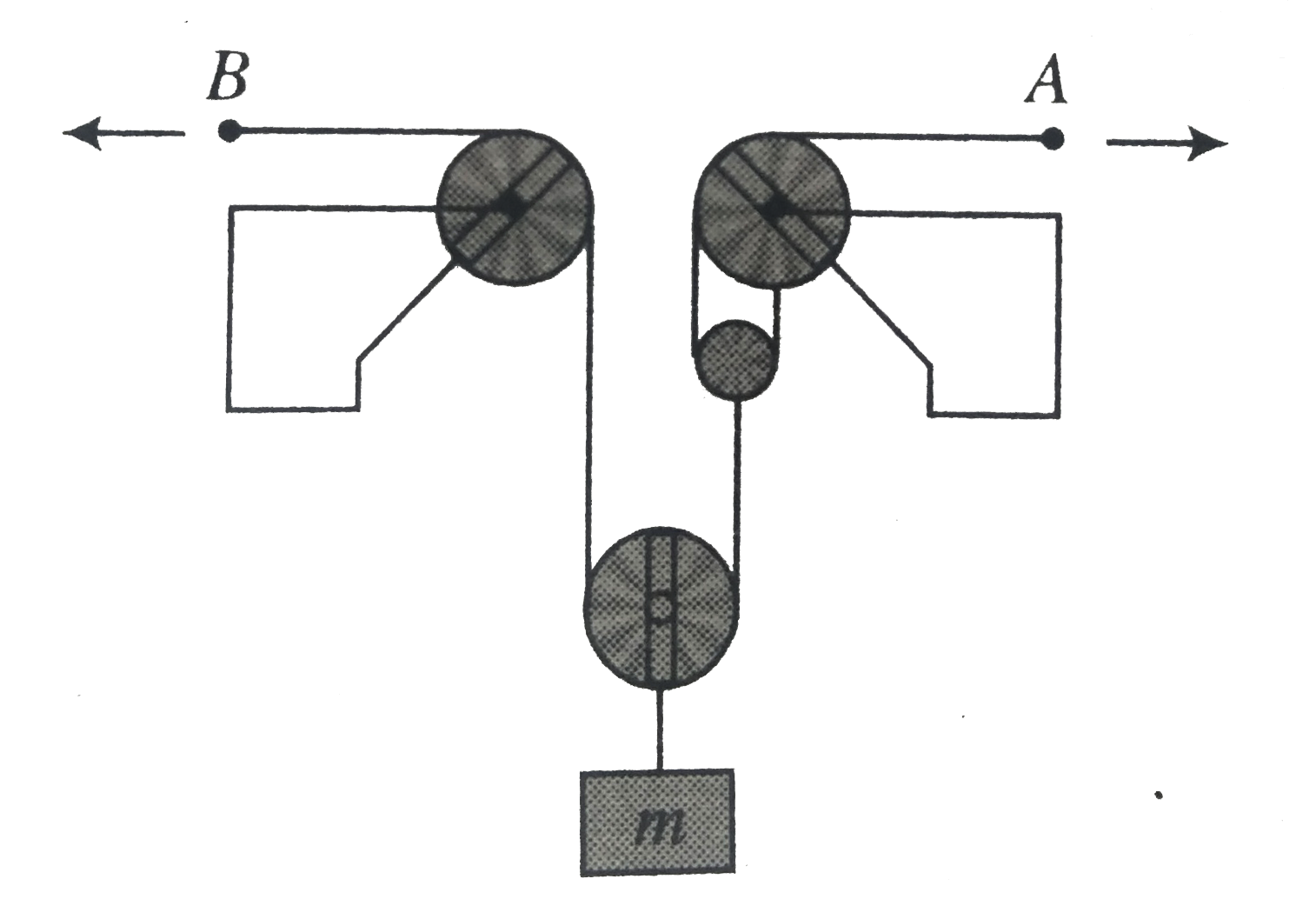 04:43View Solution
04:43View SolutionConsider the situation shown in figure. All the surface are smooth. The tension in the string connected to `2m` is.
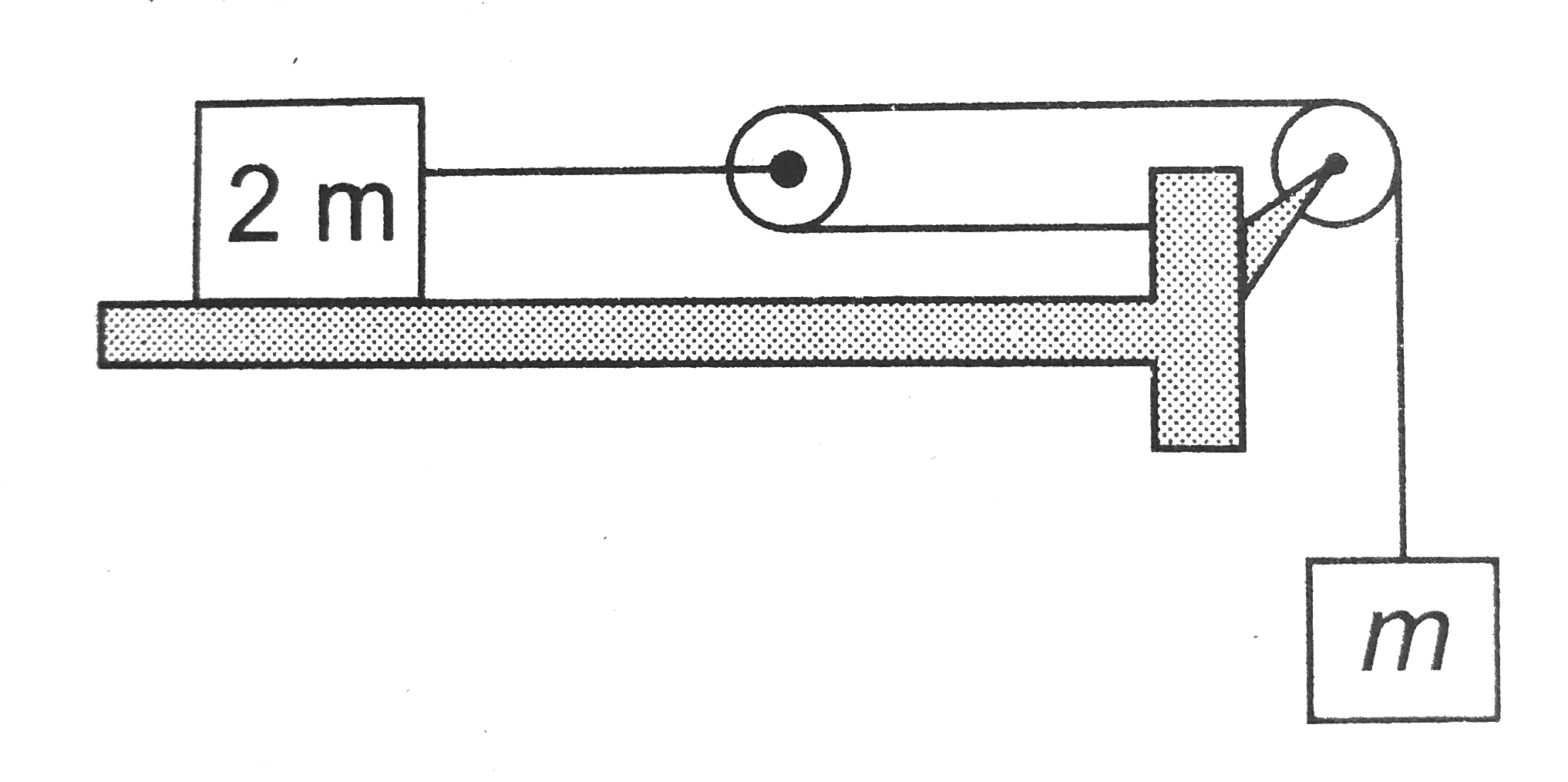 05:32View Solution
05:32View SolutionIn the figure shown neglecting friction and mass of pulley, what is the acceleration of mass `B` ?
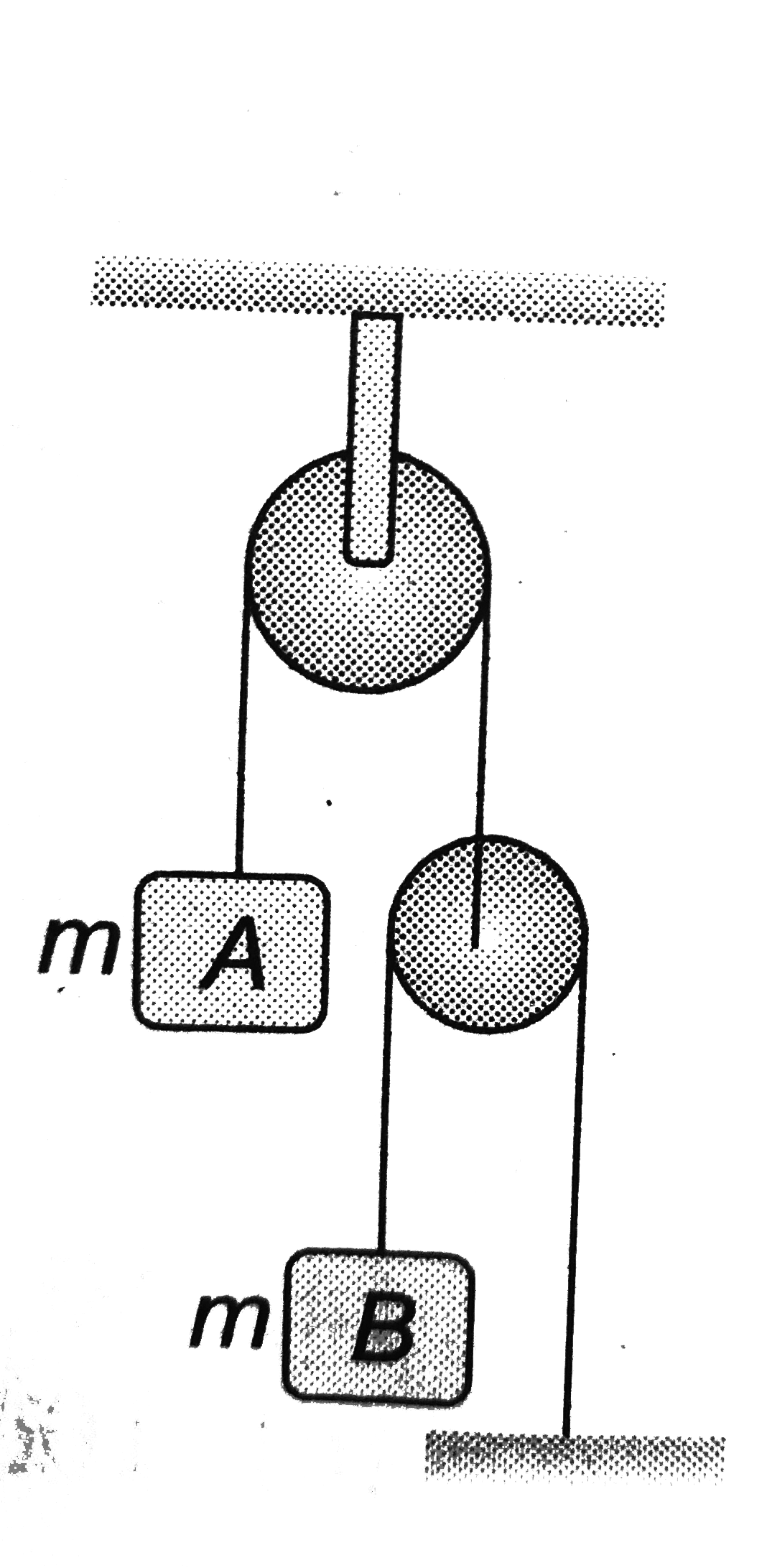 04:12View Solution
04:12View SolutionTwo block of masses `m_(1)` and `m_(2)` are connected as shown in the figure. The acceleration of the block `m_(2)` is:
 04:22View Solution
04:22View SolutionThe acceleration of the block `(A)` and `(B)` respectively in situation shown in the figure is: (pulleys and string are massless).
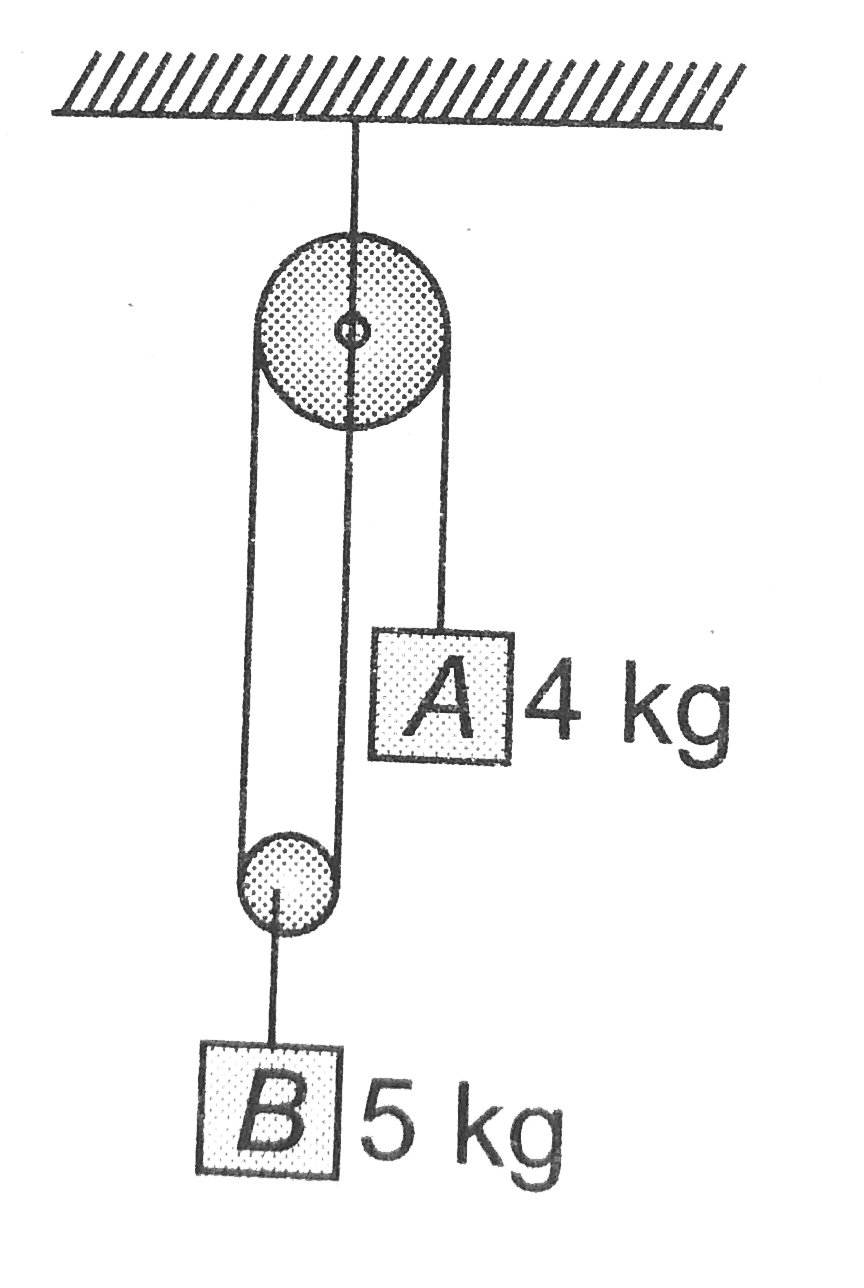 06:36View Solution
06:36View SolutionIn the system shown in figure `m_(B)=4kg` , and `m_(A)=2kg` . The pulleys are massless and friction is absent everywhere. The acceleration of block `A` is.
 05:38View Solution
05:38View SolutionThe system starts from rest and `A` attains a velocity of `5m//s` after it has moved `5m` toward right. Assuming the arrangement to be frictionless everywhere and pulley and string to be light, the value of the constant force `F` applied on `A` is:
 06:02View Solution
06:02View SolutionIn the following arrangement, the system is initially at rest. The 5-kg block is now released. Assuming the pulley and string to be massless and smooth, the acceleration of block C will be
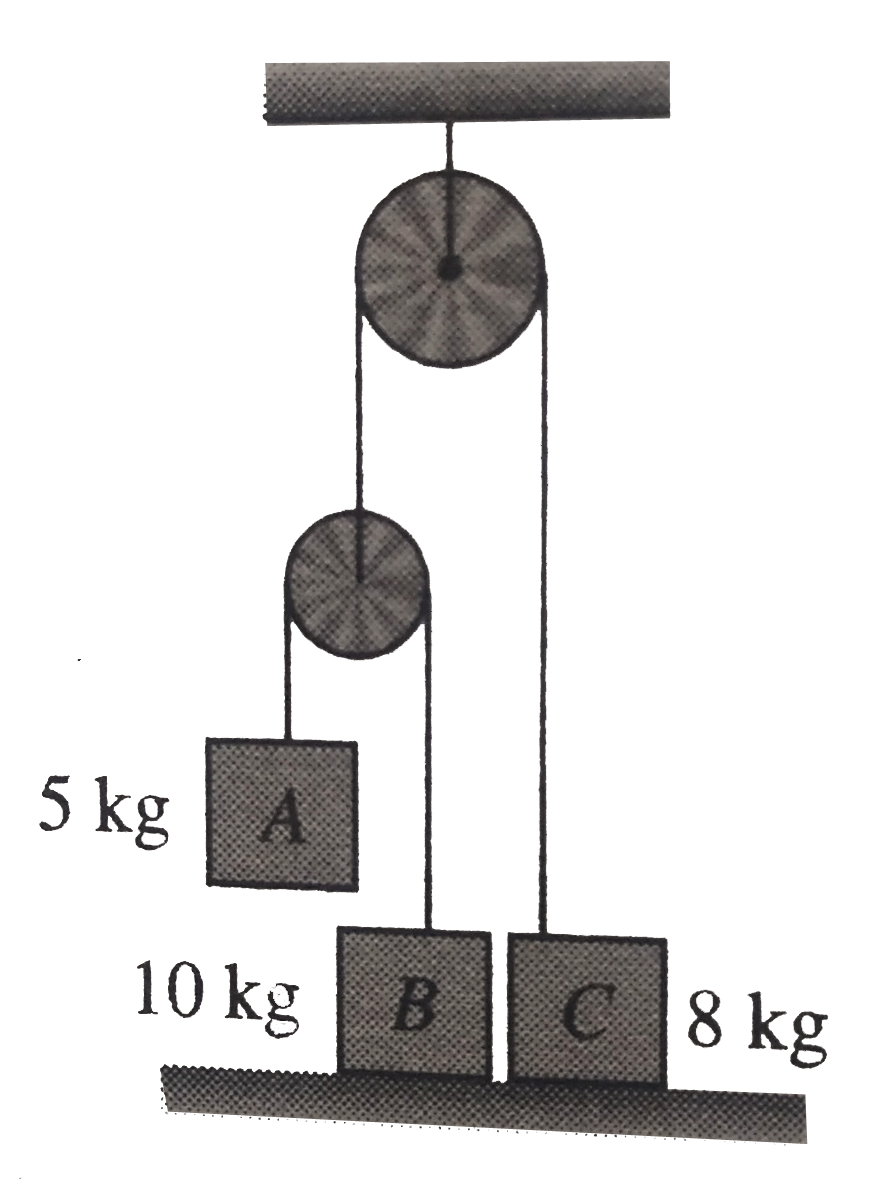 03:46View Solution
03:46View SolutionThe tension in the spring is.
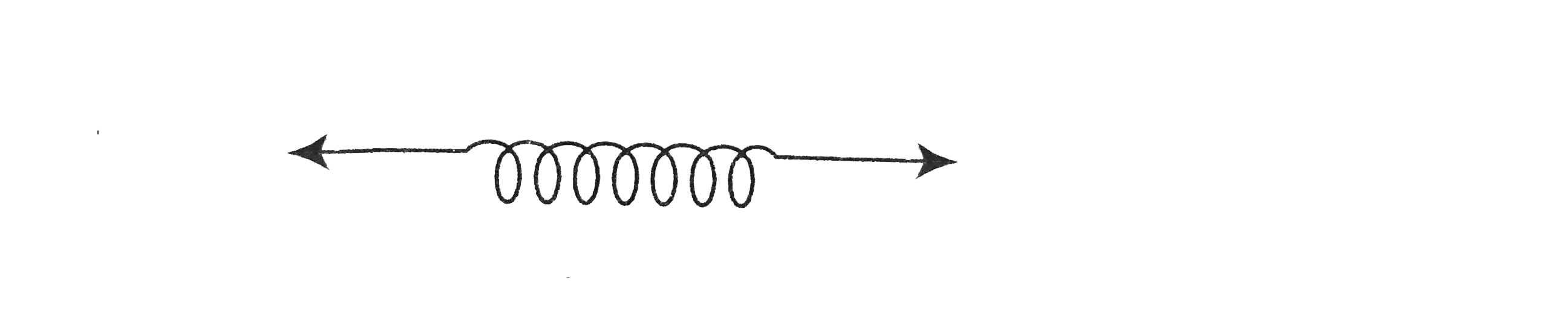 02:05View Solution
02:05View SolutionA spring balance and a physical balance are kept in a lift. In these balance equal masses are placed. If now the lift starts moving upward with constant acceleration, then.
04:08View SolutionAs shown in the figure, two equal masses each of `2kg` are suspended from a spring balance. The reading of the spring balance will be.
 02:53View Solution
02:53View SolutionA block of mass 10 kg is suspended through two light spring balances as shown in figure
 02:30View Solution
02:30View SolutionMass `m` shown in the figure is in equilibrium. If it is displaced further by `x` and released find its accleleration just after it is released. Take pulleys to be light and smooth and string light.
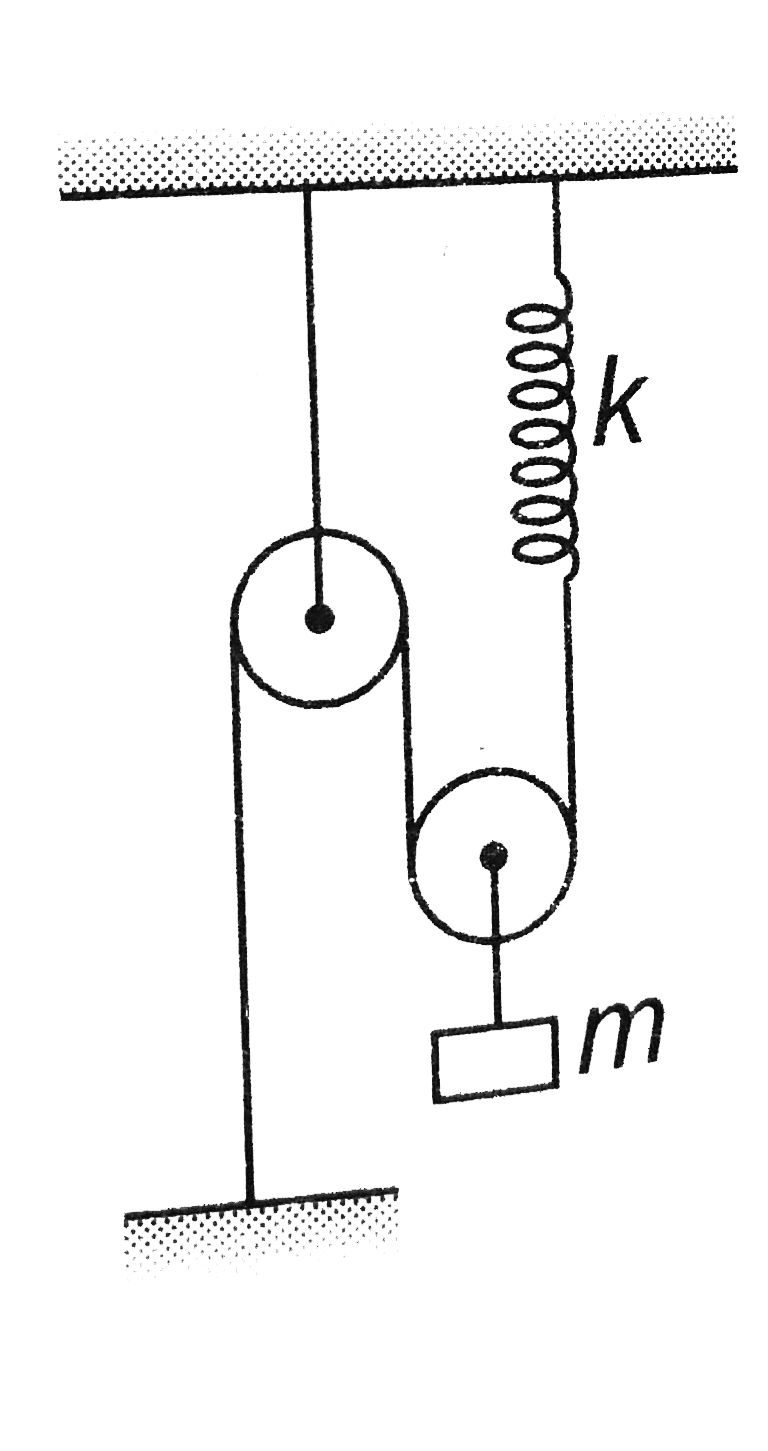 04:22View Solution
04:22View SolutionThe masses of `10kig` and `20kg` respectively are connected by a massless spring as shown in figure. A force of `200N` acts on the `20kg` mass. At the instant shown, the `10kg` mass has acceleration `12m//sec^(2)` . What is the acceleration of `20kg` mass?
 03:33View Solution
03:33View SolutionInitially the spring is un deformed. Now the force `F` is applied to `B` as shown in the figure. When the displacement of `B` w.r.t. `A` is `x` towards right in some time then relative acceleration of `B` w.r.t. `A` at that moment is:
 05:05View Solution
05:05View SolutionThe string between blocks of mass m and 2m is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass 2m and m (immediately after cutting)
 04:44View Solution
04:44View SolutionTwo block of mass `2kg` are connected by a massless ideal spring of spring constant `K=10N//m` . The upper block is suspended from roof by a light string `A` . The system shown is in equilibrium. The string `A` is now cut, the acceleration of upper block just after the string `A` is cut will be `(g=10m//s^(2)` .
 05:24View Solution
05:24View SolutionA block `A` of mass `m` is attached at one end of a light spring and the other end of the spring is connected to another block `B` of mass `2m` through a light string as shown in the figure. `A ` is held and `B` is in static equilibrium. Now `A` is released. The acceleration of `A` just after that instant is `a` . In the next case, `B` is held and `A` is in static equilibrium. Now when `B` is released, its acceleration immediately after the release is `b` . The value of `a//b` is (pulley, string and the spring are massless).
 05:11View Solution
05:11View SolutionMass `m` shown in the figure is in equilibrium. If it is displaced further by `x` and released find its accleleration just after it is released. Take pulleys to be light and smooth and string light.
 04:22View Solution
04:22View SolutionSame spring is attached with `2kg` , `3kg` and `1kg` blocks in three different cases as shown in figure. If `x_(1)` , `x_(2)` and `x_(3)` be the extensions in the spring in these cases then (Assume all the block s to move with uniform acceleration).
 06:40View Solution
06:40View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant `K=((sqrt(3)+1)mg)/(R )`. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
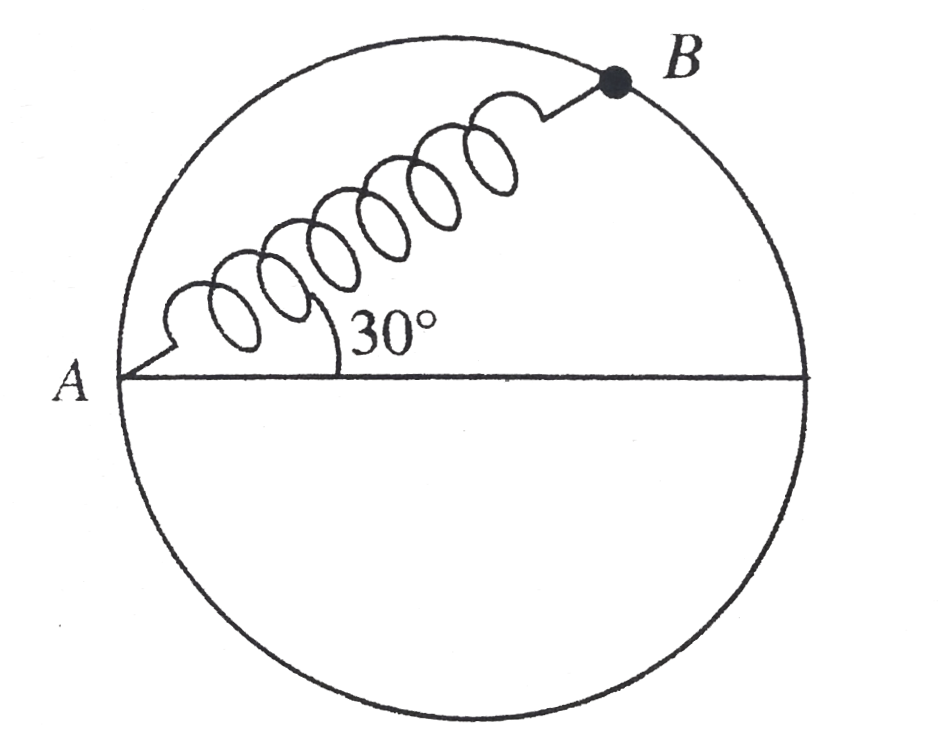 04:26View Solution
04:26View SolutionThe masses of `10kig` and `20kg` respectively are connected by a massless spring as shown in figure. A force of `200N` acts on the `20kg` mass. At the instant shown, the `10kg` mass has acceleration `12m//sec^(2)` . What is the acceleration of `20kg` mass?
 03:33View Solution
03:33View SolutionA horizontal force `F` of variable magnitude and constant direction acts on a body of mass `m` which is initially at rest at a point `O` on a smooth horizontal surface. The magnitude of `F` is given by `F=beta+alphat` where `t` is the time for which the force has been acting on the distance of the body from `O` at time `t` , then `s` is equal to.
07:40View SolutionIn the figure if block `A` and wedge `b` will move with same acceleration, then the magnitude of normal reaction between the block and the wedge will be (There is no friction between block and the wedge and the wedge moves on horizontal surface as shown.)
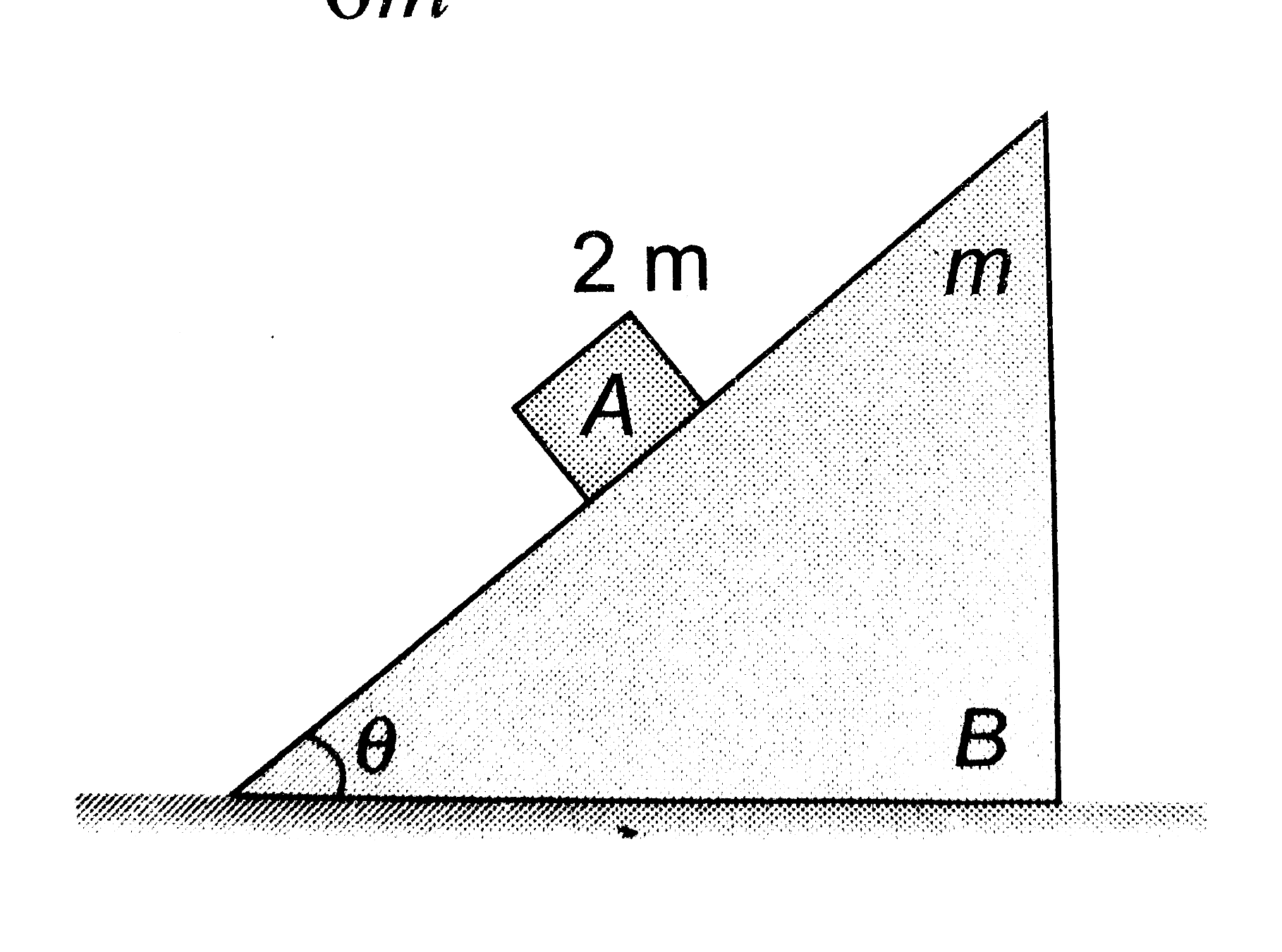 02:26View Solution
02:26View SolutionA car is moving on a plane inclined at `30^(@)` to the horizontal with an acceleration of `10m//s^(2)` parallel to the plane upward. A bob is suspended by a string from the roof. The angle in degrees which the string makes with the vertical is: (Assume that the bob does not move relative to car) `[g=10m//s^(2)]`
07:21View SolutionA solid sphere of mass 2 kg is resting inside a cube as shown in fig. The cube is moving with a velocity `vec(v)=(5t hat(i)+2t hat(j))ms^(-1)`. Here t is time in seconds. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube?
 03:23View Solution
03:23View SolutionA lift of total mass `M` is raised by cable from rest through a height `h` . The greatest tension which the cables car safely bear is `n` Mg. The maximum sped of lift during its journey if the ascent is to made in shortest time is
11:48View SolutionA block of mass `m` lies on wedge of mass `M` , which lies on fixed horizontal surface. The wedge is free to move on the horizontal surface. A horizontal force of magnitude `F` is applied on block as shown neglecting friction at all surface, the value of force `F` such that block has no relative motion w.r.t wedge will be: (Where `g` is acceleration due to gravity)
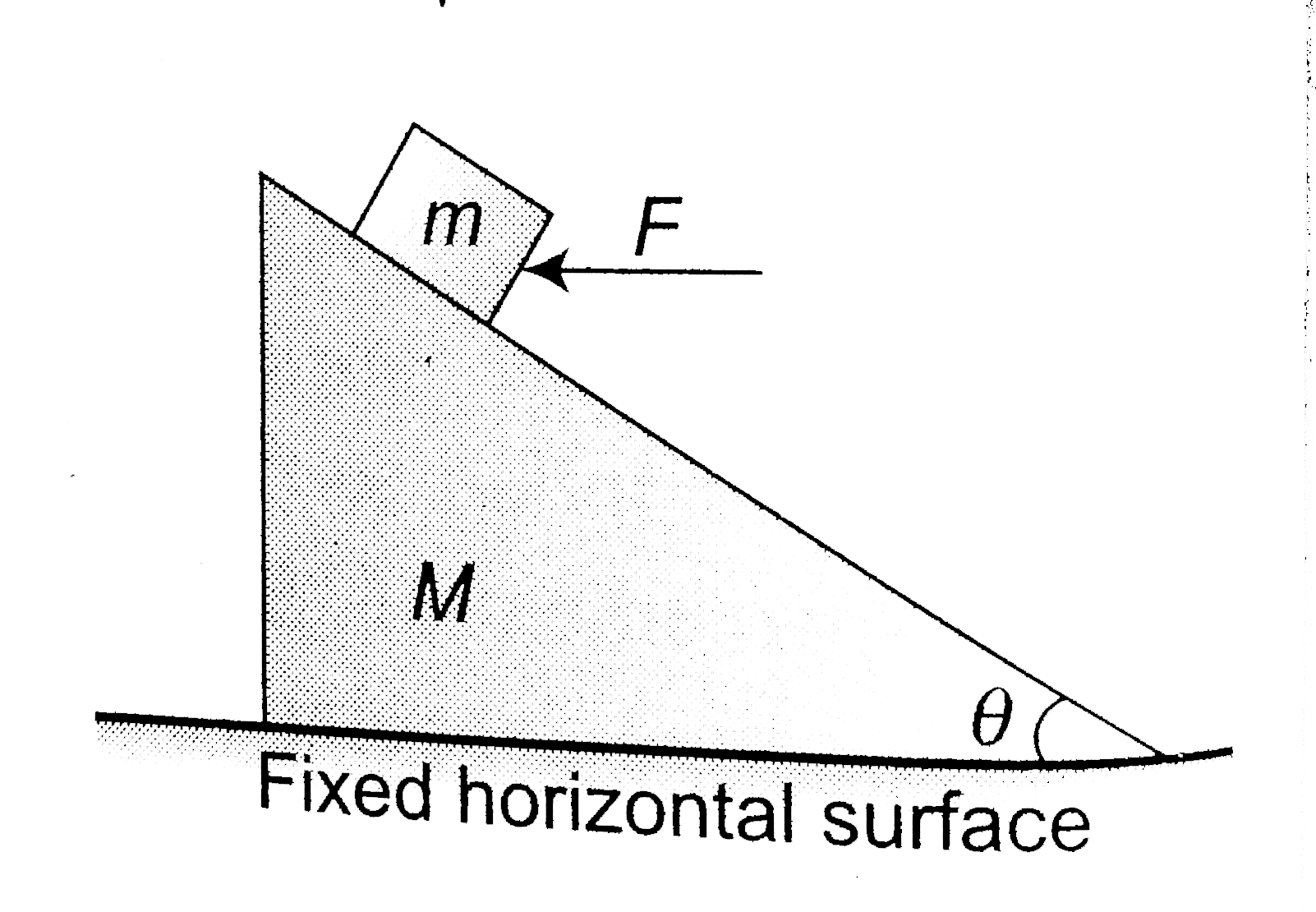 08:56View Solution
08:56View SolutionThe ratio of tensions in the string connected to the block of mass `m_(2)` in figure, respectively, is (friction is absent everywhere):`[m_(1)=50 kg, m_(2)=80kg` and `F=1000N]`
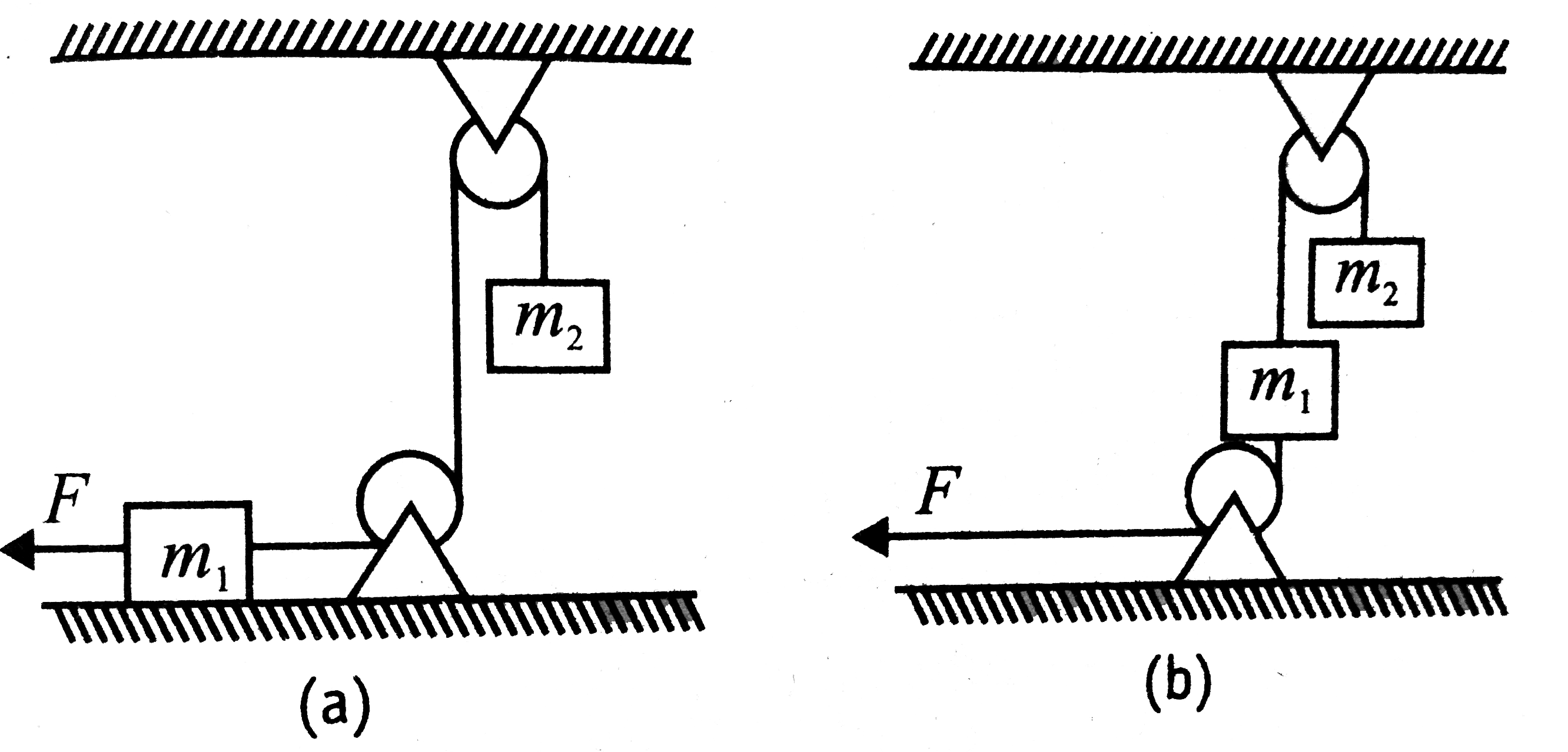 04:30View Solution
04:30View SolutionTwo unequal masses are connected on two sides of a light and smooth pulley as shown in figure. The system is released from rest. The larger mass is stopped `1.0` second after the system is set into motion and then released immediately. The time elapsed before the string is tight again is: Take `g=10m//s^(2)`
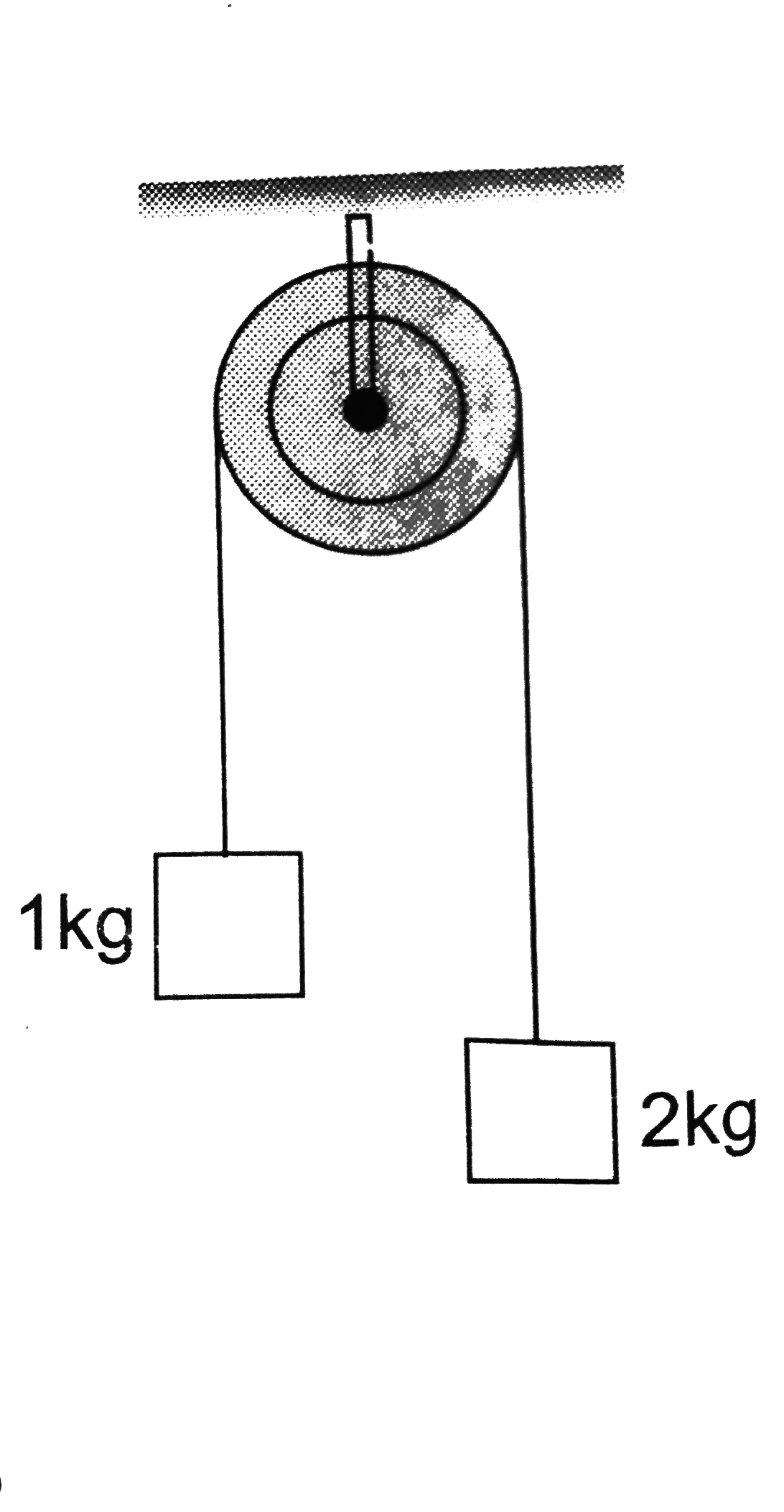 05:04View Solution
05:04View SolutionA hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponet. The force that acts on the player is.
03:51View SolutionBlock `A` of mass `2kg` is placed over a block `B` of mass `8kg` . The combination is placed on a rough horizontal surface. If `g=10ms^(-2)` , coefficient of friction between `B` and floor `=0.5`, coefficient of friction between `A` and `B=0.4` and a horizontal force of `10N` is applied on `8kg` block, then the force of friction between `A` and `B` is.
 03:35View Solution
03:35View SolutionIn the masses of A and B are 10 kg and 5 kg . Calculate the minimum mass of C which may stop A from slipping Coefficient of static friction between block A and table is 0.2
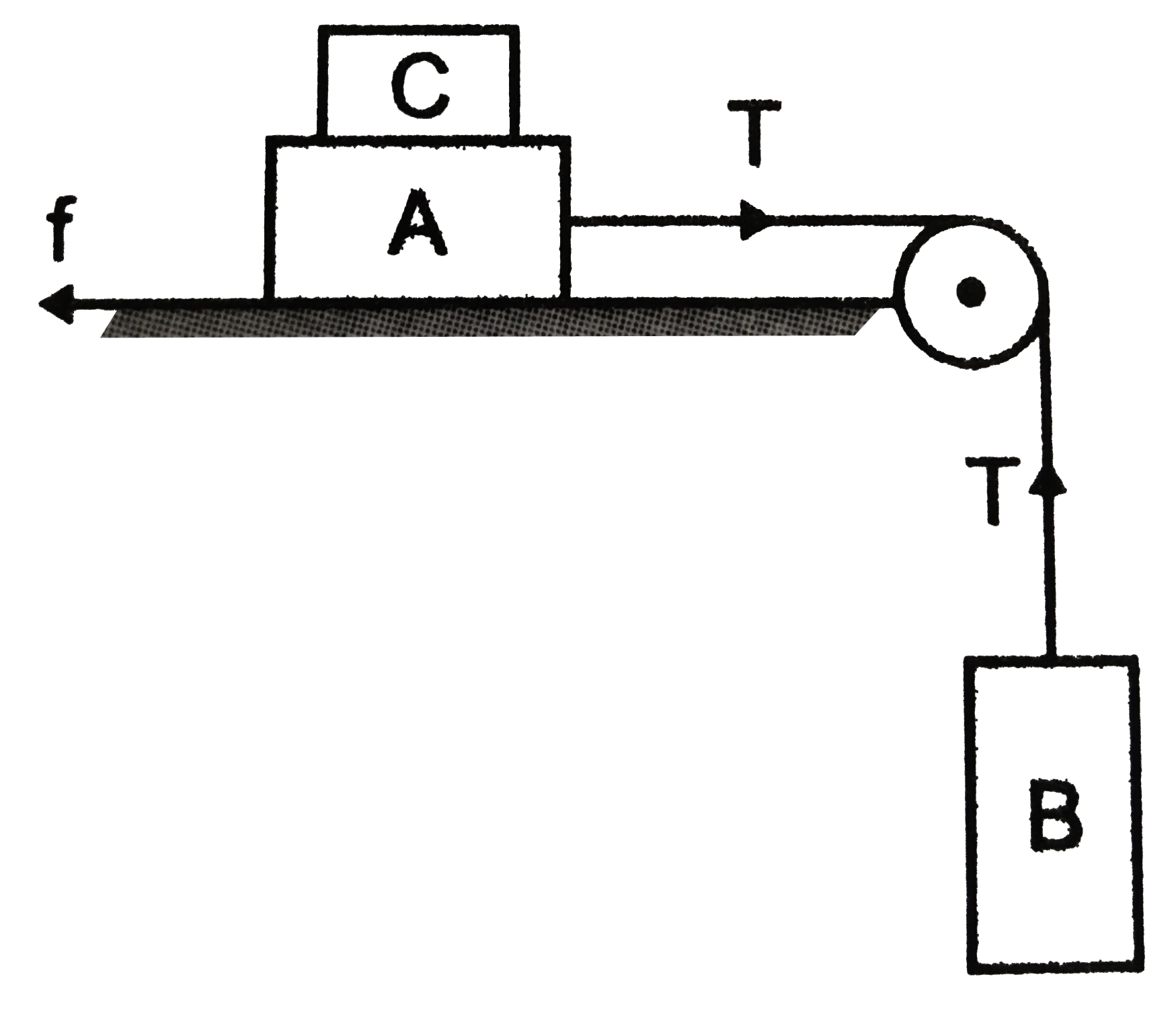 . 02:51View Solution
. 02:51View SolutionA 40kg slab rests on a frictionless floor as shown in the figure. A 10kg block rests on the top of the slab. The static coefficient of friction between the block and slab is `0.60` while the kinetic friction is `0.40` . The 10kg block is acted upon by a horizontal force 100N. if `g=9.8m//s^(2)` , the resulting acceleration of the slab will be.
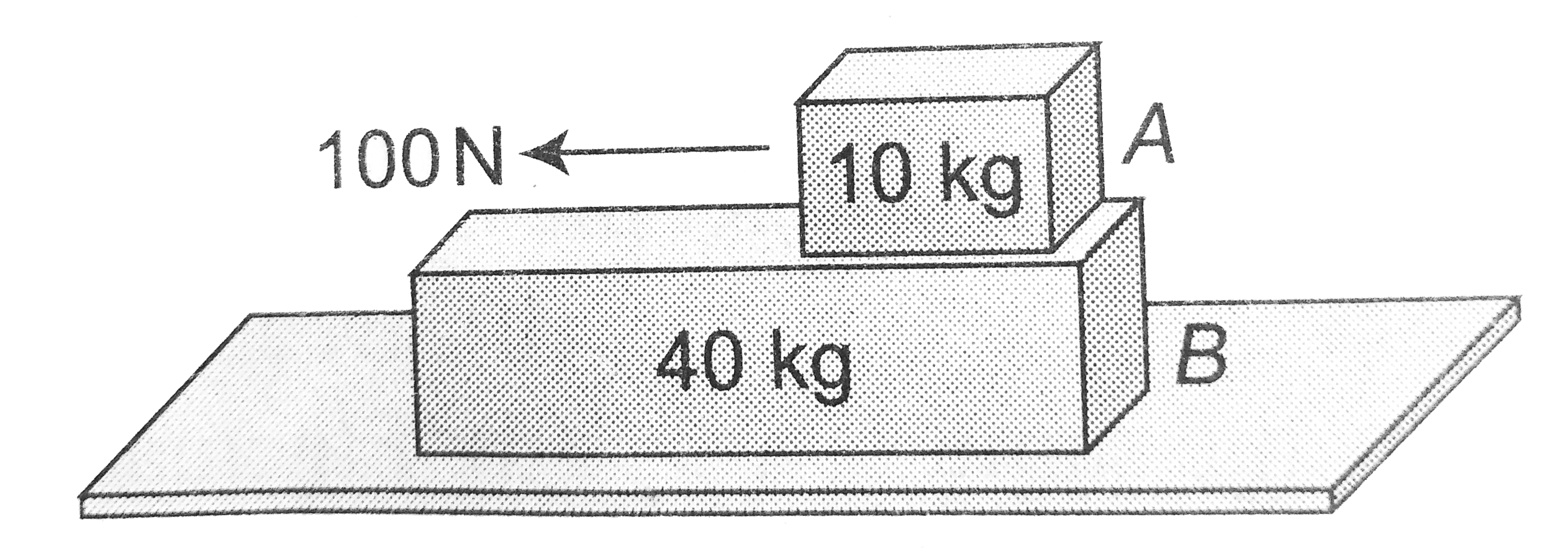 06:50View Solution
06:50View SolutionIn the arrangement shown in the figure mass of the block `B` and `A` are `2m` , `8m` respectively. Surface between `B` floor is smooth. The block `B` is connected to block `C` by means of a pulley. If the whole system is released then the minimum value of mass of the block `C` so that the block `A` remains stationary with respect to `B` is: (Coefficient of friction between `A` and `B` is `mu` and pulley is ideal).
 05:34View Solution
05:34View SolutionA flat car is given an acceleration `a_(0)=2m//s^(2)` starting from rest. A cable is connected to a crate of weight `50kg` as shown whose other end is attached to a fixed support on ground. Neglect friction between the floor and the car wheels and also the mass of the pulley. Calcuollate corresponding tension in th cable if `mu=0.30` between the crate and the floor or the car.
 03:34View Solution
03:34View SolutionIn the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is `mu=0.5` . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.
 06:35View Solution
06:35View SolutionThe coefficient of friction between the block and the horizontal surface is mu. The block moves toward right under action of horizontal force `F` (figure-a). Sometime later another force `P` is applied to the block making an angle theta `(such that tan theta=mu)` with vertical as shown in (figure-b). After application of force `P` , the acceleration of block shall.
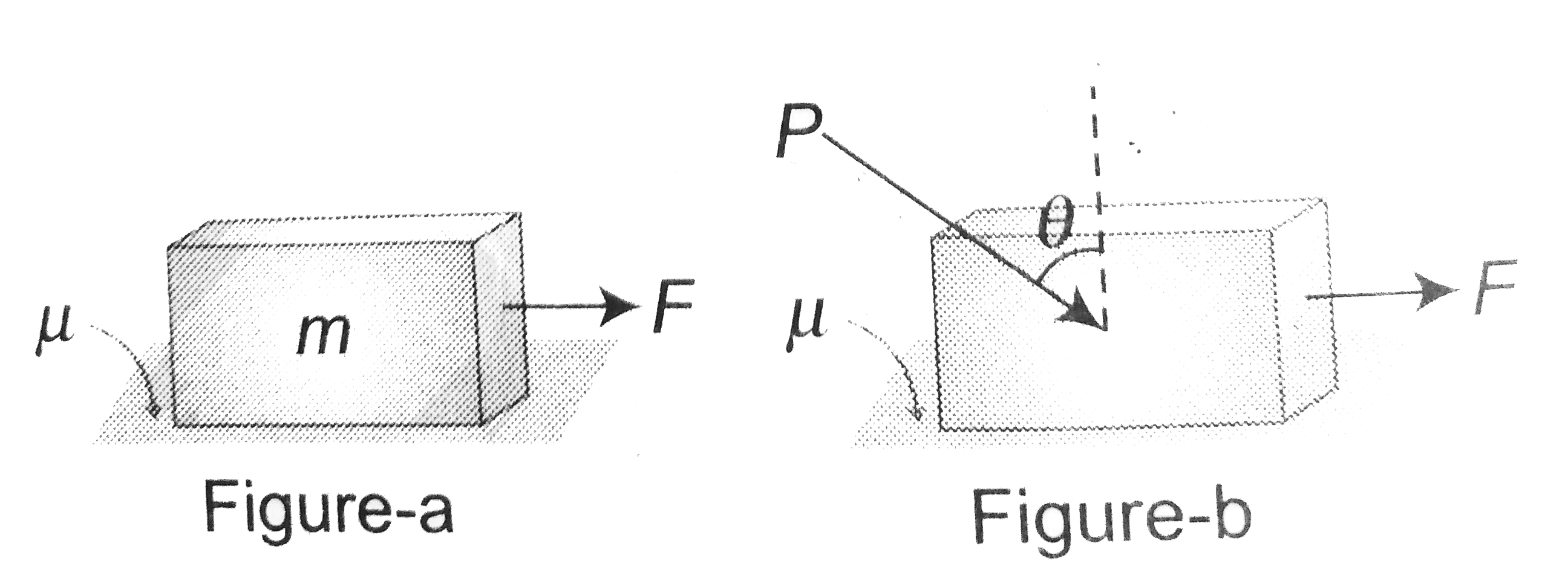 07:08View Solution
07:08View SolutionTwo blocks `A` and `B` of masses `m=10kg` and `M=20kg` respectively are planed on each other and their combination rests on a fixed horizontal surface `C` . A light string passing over the smooth light pulley is used to contact `A` and `B` as shown. The coefficient of sliding friction between all surface in contact is `mu=(1)/(4)` . if `A` is dragged with a force `F` then for both `A` and `B` to move with a uniform speed we have.
 09:27View Solution
09:27View SolutionIn the pulley arrangement shown in Fig the pulley `p_(2)` is movable .Assuming the coefficient of friction between `m` and surface to be `muu` the minimum value of `M` for which `m` is at rest is
 02:55View Solution
02:55View SolutionA block placed on a horizontal surface is being pushed by a force F making an angle `theta` with the vertical. If the friction coefficient is `mu`. How much force is needed to get the block just started.
06:26View SolutionA system is pushed by a force `F` as shown in figure All surfaces are smooth except between `B` and `C` is `mu`. Minimum value fo `F` to prevent block `B` from down ward slipping is
 04:14View Solution
04:14View SolutionAssertion: A rocket works on the principle of conservation of linear momentum.
Reason: Wheneven there is a change in momentum of one body, the same change occurs in the momentum of the second body of the same system but in the opposite directio.02:08View Solution
Problems Based On Mixed Concepts questions and complete solutions for chapter NEWTONS LAWS OF MOTION of A2Z PHYSICS (HINGLISH) of Class 11
