Complete Solutions to Level 1 of chapter CALORIMETRY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY |
| ARIHANT MASTER PROBLEM | Level 1 |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
You are on a picnic and you make tea for yourself and your friend. However, your friend has gone out to bring something for you. You observed that the fire (that you ignited for making tea) has heated two nearby blocks of stones – one of sand stone and other of granite – to `90^(@)C`. Both blocks have nearly same mass but granite has higher specific heat than marble. To keep the tea hot for your friend you decided to place the tea pot on one of the stones. Which stone will you choose – granite or marble?
View SolutionAn electric kettle is filled with `1.3 kg` of water at `20^(@)C`. The power of the heating coil of the kettle is 2.0 KW. After switching it on the water begins to boil in `220s` . If the kettle was kept on for a further interval of `Delta t` it was observed that only 200g water remained in the kettle and remaining water vaporized (the vapor is allowed to escape through a small vent). The specific latent heat of vaporization of water at `100^(@)C` (boiling point) is `L = 2.26 KJ//g`. Calculate the specific heat capacity of water and the interval `Delta t`. Assume that heat supplied by the heater is completely absorbed by the water.
View SolutionA heavy machine rejects a liquid at `60^(@)C` which is to be cooled to `30^(@)C` before it is fed back to the machine. The liquid rejected by the machine is kept flowing through a long tube while it is cooled by 60 liter water surrounding the tube. The initial temperature of the cooling water is `10^(@)C` and it is `20^(@)C` when it is changed after 1 hour. Calculate the amount of liquid that passes through the tube in one hour. Specific heat capacity of the liquid and water are `0.5 calg^(-1) .^(@)C^(-1)` and `1.0 calg^(-1).^(@)C^(-1)` respectively.
View SolutionA solid metal cube has side length L and density d. Its specific heat capacity and coefficient of linear expansion are s and `alpha` respectively. How much heat must be added to the cube to increase its volume by `2 %`?
View SolutionA certain mass of a solid exists at its melting temperature of `20^(@)C`. When a heat Q is added `(4)/(5)` of the material melts. When an additional Q amount of heat is added the material transforms to its liquid state at `50^(@)C`. Find the ratio of specific latent heat of fusion (in `J//g`) to the specific heat capacity of the liquid (in `J g^(-1) .^(@)C^(-1)`) for the material.
View SolutionThe temperature of samples of three liquids A, B and C are `12^(@)C`, `19^(@)C` and `28^(@)C` respectively. The temperature when A and B are mixed is `16^(@)C` and when B and C are mixed it is `23^(@)C`.
(i) What should be the temperature when A and C are mixed?
(ii) What is final temperature if all the three liquids are mixed?
Assume no heat loss to the surrounding.
View SolutionA table top is made of aluminium and has a hole of diameter 2 cm. An iron sphere of diameter 2.004 m is resting on this hole. Below the hole, an insulated container has 2 kg of water in it. Everything is at ambient temperature of `25^(@)C`. The table top along with the iron sphere is heated till the ball falls through the hole into the water. Find the equilibrium temperature of the ball and water system
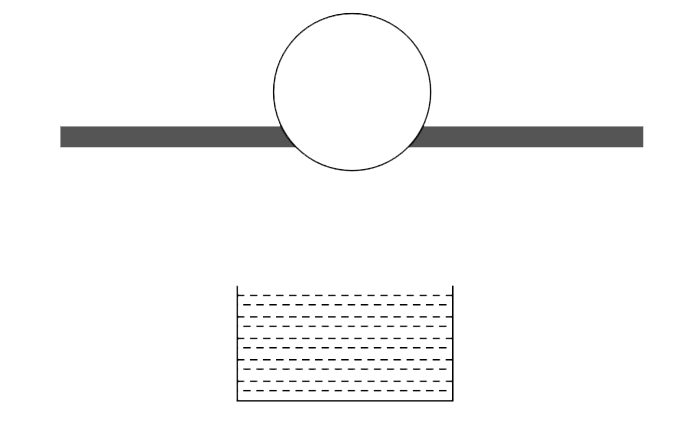
Neglect any heat loss from ball–water system to the surrounding and assume the heat capacity of the container to be negligible.
Relevant data: Coefficient of linear expansion for aluminium and iron are `2.4 xx 10^(-5) .^(@)C^(-1)` and `1.2 xx 10^(-5) .^(@)C^(-1)` respectively. Specific heat capacity of water and iron are `4200 J .^(@)C^(-1) g^(-1)` and `450 J .^(@)C^(-1) g^(-1)` respectively. Density of iron at `25^(@)C` is `8000 kg//m^(3)`.
View SolutionA 50 g ice at `0^(@)C` is added to 200 g water at `70^(@)C` taken in a flask. When the ice has melted completely, the temperature of the flask and the contents is reduced to `40^(@)C`. Now to bring down the temperature of the contents to `20^(@)C`, find a further amount of ice that is to be added.
View SolutionThe latent heat of vaporization of water at its boiling point is `L_(V)`. But water can evaporate at temperatures below the boiling point – for example it evaporates at body temperature when you perspire. Will the energy needed to evaporate unit mass of water at body temperature be more than or less than `L_(V)`?
View SolutionA vessel contains a small amount of water at `0^(@)C`. If the air in the vessel is rapidly pumped out, it causes freezing of the water. Why? What percentage of the water in the container can be frozen by this method? Latent heat of vaporization and fusion are `L_(V) = 540 cal g^(-1)` and `L_(f) = 80 cal g^(-1)` respectively.
View SolutionA vessel containing 100 g ice at `0^(@)C` is suspended in a room where temperature is `35^(@)C`. It was found that the entire ice melted in 10 hour. Now the same vessel containing 100 g of water at `0^(@)C` is suspended in the same room. How much time will it take for the temperature of water to rise to `0.5^(@)C`. Neglect the heat capacity of the vessel. Specific heat of water and specific latent heat of fusion of ice are `1 cal g^(-1) .^(@)C^(-1)` and `80 cal g^(-1)` respectively.
View SolutionA calorimeter of negligible heat capacity contains ice at `0^(@)C`. 50 g metal at `100^(@)C` is dropped in the calorimeter. When thermal equilibrium is attained the volume of the content of the calorimeter was found to reduce by `0.5 xx 10^(-6) m^(3)`. Calculate the specific heat capacity of the metal. Neglect the change in volume of the metal. Specific latent heat of fusion of ice is `L = 300 xx 10^(3) J kg^(-1)` and its relative density is 0.9.
View SolutionA refrigerator converts 1.3 kg of water at `20^(@)C` into ice at `-15^(@)C` in 1 hour. Calculate the effective power of the refrigerator. Specific latent heat of fusion of ice `= 3.4 xx 10^(5) J kg^(-1)` Specific heat capacity of water `= 4.2 xx 10^(3) J kg^(-1) K^(-1)` Specific heat capacity of ice `= 2.1 xx 10^(3) J kg^(-1) K^(-1)`
View SolutionA calorimeter of water equivalent 10 g contains a liquid of mass 50 g at `40 .^(@)C`. When m gram of ice at `-10^(@)C` is put into the calorimeter and the mixture is allowed to attain equilibrium, the final temperature was found to be `20^(@)C`. It is known that specific heat capacity of the liquid changes with temperature as `S = (1+(theta)/(500)) cal g^(-1) .^(@)C^(-1)` where `theta` is temperature in `.^(@)C`. The specific heat capacity of ice, water and the calorimeter remains constant and values are `S_("ice") = 0.5 cal g^(-1) .^(@)C^(-1), S_("water") = 1.0 cal g^(-1) .^(@)C^(-1)` and latent heat of fusion of ice is `L_(f) = 80 cal g^(-1)`. Assume no heat loss to the surrounding and calculate the value of m.
View SolutionA well insulated container has a mixture of ice and water, at `0^(@)C`. The mixture is supplied heat at a constant rate of 420 watt by switching on an electric heater at time t = 0. The temperature of the mixture was recorded at time t = 150s, 273s and 378s and the readings were `0^(@)C`, `10^(@)C` and `20^(@)C` respectively. Calculate the mass of water and ice in the mixture. Specific heat of water `= 4.2 J g^(-1) .^(@)C^(-1)`, Specific latent heat of fusion of ice `= 336 J g^(-1)`. Assume that the mixture is stirred slowly to maintain a uniform temperature of its content.
View SolutionAn insulated container has 60 g of ice at `-10^(@)C`. 10 g steam at `100^(@)C`, sourced from a boiler, is mixed to the ice inside the container. When thermal equilibrium was attained, the entire content of the container was liquid water at `0^(@)C`. Calculate the percentage of steam (in terms of mass) that was condensed before it was fed to the container of ice. Specific heat and latent heat values are
`S_("ice") = 0.5 cal g^(-1) .^(@)C^(-1)`, `S_("water") = 1.0 cal g^(-1) .^(@)C^(-1)`
`L_("fusion") = 80 cal g^(-1)`, `L_("vaporization") = 540 cal g^(-1)`
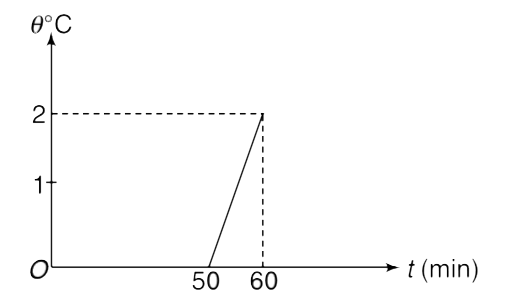
View SolutionA container contains 5 kg of water at `0^(@)C` mixed to an unknown mass of ice in thermal equilibrium. The water equivalent of the container is 100 g. At time t = 0, a heater is switched on which supplies heat at a constant rate to the container. The temperature of the mixture is measured at various times and the result has been plotted in the given figure. Neglect any heat loss from the mixture – container system to the surrounding and calculate the initial mass of the ice.
Given: `S_(p)`. latent heat of fusion of ice is `L_(f) = 80 cal g^(-1)`
`S_(p)`. heat capacity of water `= 1 cal g^(-1) .^(@)C^(-1)`
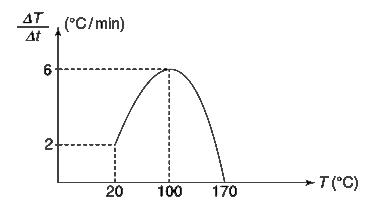
View SolutionA liquid kept in a beaker is supplied heat. The rate of change of temperature of the liquid is plotted versus its temperature. Which intrinsic property of the liquid can be inferred from the graph? What is its value?
View SolutionA meteorite has mass of 500 kg and is composed of a metal. The temperature of the meteor is `-20^(@)C` and its speed is 10 km/hr when it is at large distance from a planet. The meteorite crashes into the planet and its entire kinetic energy gets converted into heat. This heat is equally shared between the planet and the meteorite. Assume that the heating of meteorite is uniform and the average specific heat capacity of the metal, for its solid, liquid and vapour phase, is `1200 J kg^(-1) .^(@)C^(-1)`. The latent heat of fusion and vaporization of the metal are `L_(f) = 4 xx 10^(5) J kg^(-1)` and `L_(v) = 1.1 xx 10^(7) J kg^(-1)` respectively. The melting point and boiling points are `380 .^(@)C` and `2380 .^(@)C` respectively. Find the temperature of the meteorite material immediately after the impact.
Take: `G = 6.6 xx 10^(11) N m^(2) kg^(-2)`, mass of planet `M = 6 xx 10^(24) kg`, radius of planet R = 6600 km
View Solution100 g of ice at `-40^(@)C` is supplied heat using a heater. The heater is switched on at time t = 0 and its power increases linearly for first 60 second and thereafter it becomes constant as shown in the graph. Heater is kept on for 5 minutes. The specific heat capacity for ice and water are known to be `2.1 (J)/(g^(@)C)` and `4.2 (J)/(g^(@)C)` respectively. The specific latent heat for fusion of ice is `336 J//g`.
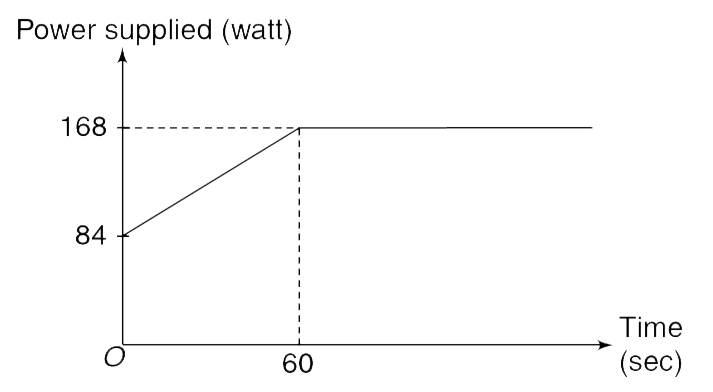
The temperature of the ice sample kept on increasing till time `t_(1)` and then remained constant in the interval `t_(1) lt t lt t_(2)`.
(i) Find `t_(1)` and `t_(2)`
(ii) Find final temperature of the sample when the heater is switched off.
View Solution
Level 1 questions and complete solutions for chapter CALORIMETRY of ARIHANT PHYSICS (HINGLISH) of Class 11