Complete Solutions to Level 2 of chapter CALORIMETRY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY |
| ARIHANT MASTER PROBLEM | Level 2 |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
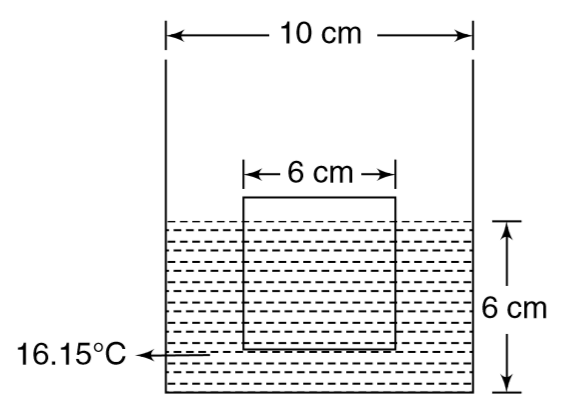
A container has a square cross-section of `10 cm xx 10 cm`. A cubical ice block of side length 6 cm is floating in water in the container. Water level in the container is 6 cm high. The ice block is at a temperature of `0^(@)C` and the water is at `16.15^(@)C`. Assume that heat exchange take place between the ice block and water only. What length of ice block will remain submerged in water when the system reaches thermal equilibrium? Assume that the ice block maintains its cubical shape as it melts. Take - density of ice `= 0.9 g//c c`, density of water = `1.0 g//c c`
Specific heat capacity of water `= 1 cal g^(-1) .^(@)C^(-1)`, Specific latent heat of fusion of ice `= 80 cal g^(-1)`
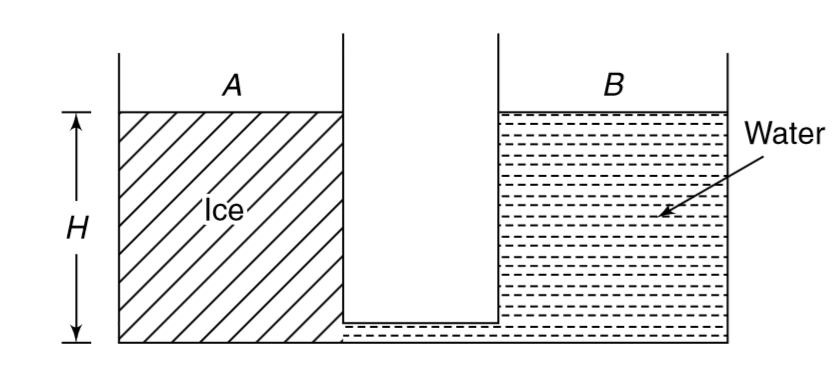
View SolutionTwo identical cylindrical containers A and B are interconnected by a tube of negligible dimensions. Container A is filled with an ice block up to height H = 1.8 m and container B is filled up to same height with water. Ice is at `0^(@)C` and water is at `40^(@)C`. Due to heat exchange between water and ice, the ice block begins to melt. Assume that the ice block melt in horizontal layers starting from the bottom. The thickness of ice block reduces uniformly over the entire cross section of the container. The ice block moves without friction inside the container and no water enters between the vertical wall of the container and the ice block. Heat is exchanged only between the ice block and the water and there is no heat exchange with containers or atmosphere. Calculate the height of water in container B when thermal equilibrium is attained. Relative density and specific latent heat of fusion of ice are 0.9 and `80 cal g^(-1)` respectively. Specific heat capacity of water is `1 cal g^(-1) .^(@)C^(-1)`.
View SolutionA well insulated box has two compartments A and B with a conducting wall between them. 100 g of ice at `0^(@)C` is kept in compartment A and 100 g of water at `100^(@)C` is kept in B at time t = 0. The temperature of the two parts A and B is monitored and a graph is plotted for temperatures `T_(A)` and `T_(B)` versus time (t) [Fig. (b)]. Assume that temperature inside each compartment remains uniform.
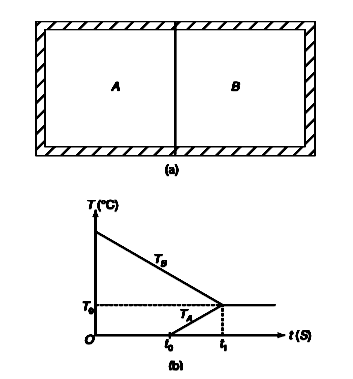
(a) Is it correct to assert that the conducting wall conducts heat at a uniform rate, irrespective of the temperature difference between A and B?
(b) Find the value of time `t_(1)` and temperature `T_(0)` shown in the graph, if it is known that `t_(0) = 200 s`.
Specific heat of ice `= 0.5 cal g^(-1) .^(@)C^(-1)`
Specific heat of water `= 1.0 cal g^(-1) .^(@)C^(-1)`
Latent heat of fusion of ice `= 80 cal g^(-1)`
View SolutionAn ice ball has a metal piece embedded into it. The temperature of the ball is `-theta^(@)C` and it contains mass M of ice. When placed in a large tub containing water at `0^(@)C`, it sinks. Assume that the water in immediate contact with the ice ball freezes and thereby size of the ball grows. What is the maximum possible mass of the metal piece so that the ball can eventually begin to float. Densities of ice, water and metal are `sigma, rho` and d respectively. Specific heat capacity of ice is s and its specific latent heat is L. Neglect the heat capacity of the metal piece.
View SolutionWater from a reservoir maintained at a constant temperature of `80^(@)C` is added at a slow and steady rate of m `= 3 gs^(-1)` to a calorimeter initially containing 1000 g of water at `20^(@)C`. The water in the calorimeter is stirred slowly to make the temperature uniform. Assume heat loss to the surrounding and work done in stirring is negligible and heat capacity of the calorimeter is negligible. Write the temperature of water in the calorimeter as a function of time.
View SolutionA cylindrical container has a cross sectional area of `A_(0) = 1 cm^(2)` at `0^(@)C`. A scale has been marked on vertical surface of the container which shows correct reading at `0^(@)C`. A liquid is poured in the container. When the liquid and container is heated to `100^(@)C`, the scale shows the height of the liquid as 83.33 cm. The coefficient of volume expansion for the liquid is `gamma = 0.001^(@)C^(-1)` and the coefficient of linear expansion of the material of cylindrical container is `alpha = 0.0005^(@)C^(-1)`. A beaker has `300 cm^(3)` of same liquid at `0^(@)C`. The two liquids are mixed. Find the final temperature of the mixture assuming that heat exchange takes place between the liquids only, and its specific heat capacity is independent of temperature
View Solution
Level 2 questions and complete solutions for chapter CALORIMETRY of ARIHANT PHYSICS (HINGLISH) of Class 11