Complete Solutions to Level 1 of chapter ELASTICITY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ELASTICITY |
| ARIHANT MASTER PROBLEM | Level 1 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
Human bones remain elastic if strain is less than 0.5%. However, the young’s modulus for compression `(Y_(c))` and stretch `(Y_(s))` are different. The typical values are `Y_(c) = 9.4 xx 10^(9) Pa` and `Y_(s) = 16 xx 10^(9) Pa`. The shear modulus of elasticity for the bone is `h = 10^(10) Pa` Answer following questions with regard to a leg bone of length `20 cm` and cross sectional area `3 cm^(2)`
(a) Calculate the maximum stretching force that the bone can sustain and still remain elastic.
(b) A man of mass 60 kg jumps from a height of 10 m on a concrete floor. Half his momentum is absorbed by the impact of the floor on the particular bone we are talking about. The impact lasts for 0.02 s. Will the compressive stress exceed the elastic limit?
(c) How much shearing force will be needed to break the bone if breaking strain is `5^(@)C`.
View SolutionThe elastic limit and ultimate strength for steel is `2.48 xx 10^(8) Pa` and `4.89 xx 10^(8) Pa` respectively. A steel wire of 10 m length and 2 mm cross sectional diameter is subjected to longitudinal tensile stress. Young’s modulus of steel is `Y = 2 xx 10^(11) Pa`
(a) Calculate the maximum elongation that can be produced in the wire without permanently deforming it. How much force is needed to produce this extension?
(b) Calculate the maximum stretching force that can be applied without breaking the wire.
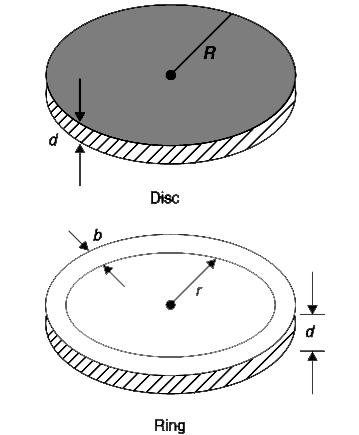
View SolutionA steel ring is to be fitted on a wooden disc of radius R and thickness d. The inner radius of the ring is r which is slightly smaller than R. The outer radius of the ring is r + b and its thickness is d (same as the disc). There is no change in value of b and d after the ring is fitted over the disc, only the inner radius becomes R. If the Young’s modulus of steel is Y, calculate the longitudinal stress developed in it. Also calculate the tension force developed in the ring.
[Take `b lt lt r`]
View SolutionA water tank is supported by four pillars. The pillars are strong enough to sustain ten times the stress developed in them when the tank is completely full. An engineer decides to increase the every dimension of the tank and the pillars by hundred times so as to store more water. Do you think he has taken a right decision? Assume that material used in construction of the tank and pillars remain same.

View SolutionTwo bars A and B are stuck using an adhesive. The contact surface of the bars make an angle q with the length. Area of cross section of each bar is `S_(0)`. It is known that the adhesive yields if normal stress at the contact surface exceeds `sigma_(0)`. Find the maximum pulling force F that can be applied without detaching the bars.

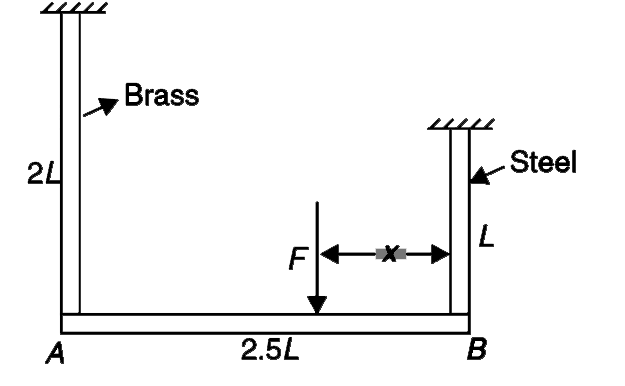
View SolutionA very stiff bar (AB) of negligible mass is suspended horizontally by two vertical rods as shown in figure. Length of the bar is 2.5 L. The steel rod has length L and cross sectional radius of r and the brass rod has length 2L and cross sectional radius of 2r . A vertically downward force F is applied to the bar at a distance x from the steel rod and the bar remains horizontal. Find the value of x if it is given that ratio of Young’s modulus of steel and brass is `(Y_(s))/(Y_(B)) = 2`.
View SolutionA closed steel cylinder is completely filled with water at `0^(@)C`. The water is made to freeze at `0^(@)C`. Calculate the rise in pressure on the cylinder wall. It is known that density of water at `0^(@)C` is `1000 kg//m^(3)` and the density of ice at `0^(@)C` is `910 kg//m^(3)`. Bulk modulus of ice at `0^(@)C` is nearly `9 xx 10^(9) Pa`. [Compare this pressure to the atmospheric pressure. Now you can easily understand why water pipelines burst in cold regions as the winter sets in.]
View Solution(i) Two identical rods, one of steel, the other of copper, are stretched by an identical amount. On which operation more work is expended?
(ii) Two identical rods, one of steel, the other of copper, are stretched with equal force. On which operation is more work needed?
View Solution
Level 1 questions and complete solutions for chapter ELASTICITY of ARIHANT PHYSICS (HINGLISH) of Class 11