Complete Solutions to उदाहरण of chapter सम्मिश्र संख्याएँ of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | सम्मिश्र संख्याएँ |
| BALAJI PUBLICATION | उदाहरण |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
हल कीजिए -
(i) `2(i)^(2)+6i^(3)+3i^(16)-6i^(19)+4i^(25)` (ii) `5i^(5)+4i^(4)+3i^(3)+2i^(2)+i`
View Solutionहल कीजिए -
(i) `i^(998)` (ii) `(sqrt(-1))^(90)`
View Solutionसिद्ध कीजिए कि -
(i) `1+i^(10)+i^(100)+i^(1000)=2` (ii) `i^(n)+i^(n+1)+i^(n+2)+i^(n+3)=0AA n in N`
(iii) `1+i^(10)+i^(20)+i^(30)=0` (iv) `(1)/(i)-(1)/(i^(2))-(1)/(i^(4))=0`
View Solutionसिद्ध कीजिए
`(1)/((1-i)^(2))-(1)/((1+i)^(2))=i`
View Solutionयदि `2x+3yi` तथा `2+9i` एक ही सम्मिश्र संख्या को करते है तो x व y के मान ज्ञात कीजिए ।
View Solutionनिम्नलिखित सम्मिश्र संख्याओं के वास्तविक व काल्पनिक मान ज्ञात कीजिए -
(i) `3-4i` (ii) `-2+sqrt(3)*i` (iii) `-3-4sqrt(-1)` (iv) `-9`
View Solutionx व y के मान ज्ञात कीजिए ।
(i) `3x+(2x-y)i=6-3i` (ii) `((3)/(sqrt(2))x-2)+5sqrt(2)yi=sqrt(2)`
View Solutionनिम्नलिखित सम्मिश्र संख्याओं के वास्तविक तथा काल्पनिक मानो को ज्ञात कीजिए ।
(i) `sqrt(37)+sqrt(-19)` (ii) `(23+2i)/(41)`
View Solutionदी गयी संख्याओं को `x+iy` के रूप में लिखे ।
(i) `z=(2+i)/((1+i)(1-2i))` (ii) `((1+i)^(3))/(4+3i)`
View Solution`x` व `y` के मान ज्ञात कीजिए यदि `(3x-2iy)(2+i)^(2)=10(1+i)`
View Solution`-2+3i` का योगात्मक प्रतिलोम `("additive inverse")` ज्ञात कीजिए ।
View Solutionसम्मिश्र संख्याओं `-sqrt(3)+sqrt(-2)` तथा `2sqrt(3)-i` का योग तथा गुणनफल ज्ञात कीजिए ।
View Solutionx तथा y के किन मानो के लिए निम्नलिखित संख्याएं सामान है
`x^(2)-7x+9yi` तथा `y^(2)i+20i-12`
View Solutionसिद्ध कीजिए
`(x^(2)+a^(2))^(4)=(x^(4)-6x^(2)a^(2)+a^(4))+(4x^(3)a-4xa^(3))^(2)`
View Solutionयदि `(x+iy)^(1//3)=a+ib` तब सिद्ध कीजिए `(x)/(a)+(y)/(b)=4(a^(2)-b^(2))`
View Solutionयदि `x=-5+2sqrt(-4)` तब `x^(4)+9x^(3)+35x^(2)-x+4` का मान ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए `x^(4)+4=(x+1+i)(x+1-i)(x-1+i)(x-1-i)`
View Solution`3-4i` का वर्गमूल ज्ञात कीजिए ।
View Solution`-7-24i` का वर्गमूल ज्ञात कीजिए
View Solutionनिम्नलिखित संख्याओं का वर्गमूल `a+ib` के रूप में ज्ञात कीजिए
(i) `7-6sqrt(2)i` (ii) `(33+56i)/(4)`
View Solution`(4+3sqrt(-20))^(1//2)+(4-3sqrt(-20))^(1//2)` का मान ज्ञात कीजिए ।
View Solutionनिम्नलिखित संख्या का वर्गमूल ज्ञात कीजिए ।
`((2+3i)/(5-4i)+(2-3i)/(5+4i))`
View Solution`(x^(2))/(y^(2))+(y^(2))/(x^(2))+(1)/(2i)((x)/(y)+(y)/(x))+(31)/(16)` का वर्गमूल ज्ञात कीजिए
View Solution`sqrt(i)` का मान ज्ञात कीजिए ।
View Solution`-27` का घनमूल ज्ञात कीजिए ।
View Solutionनिम्न का मान ज्ञात कीजिए ।
`((-1+sqrt(-3))/(2))^(-8)+((-1-sqrt(-3))/(2))^(-8)`
View Solutionयदि `1,omega,omega^(2)` इकाई के घनमूल है सिद्ध कीजिए कि
`(x-y)(xomega-y)(xomega^(2)-y)=x^(3)-y^(3)`
View Solution`1,omega,omega^(2)` इकाई के घनमूल है तो सिद्ध कीजिए कि -
`(1-omega+omega^(2))(1-omega^(2)+omega^(4))(1-omega^(4)+omega^(8)) . . . 2n` गुणनखण्ड `=2^(2n)`
View Solutionयदि `,omega,omega^(2)` इकाई के घनमूल है तो सिद्ध कीजिए कि -
(i) `(1-omega+omega^(2))+(1+omega-omega^(2))=4`
(ii) `(1+omega)^(3)-(1+omega^(2))^(3)=0`
(iii) `(1-omega+omega^(2))^(3)=(1+omega-omega^(2))^(3)=-8`
(iv) `(1-omega+omega^(2))^(5)+(1+omega-omega^(2))^(5)=32`
(v) `(2+5omega+2omega^(2))^(6)=(2+2omega+5omega^(2))^(6)=729`
(vi) `(1+omega)(1+omega^(2))(1+omega^(4))(1+omega^(8))=1`
View Solutionयदि `alpha,beta` इकाई के सम्मिश्र घनमूल है सिद्ध कीजिए कि -
`alpha^(4)+beta^(4)+alpha^(-1)beta^(-1)=0`
View Solutionयदि `x=a+b,y=aomega+bomega^(2),z=aomega^(2)+bomega`, तो सिद्ध कीजिए कि -
`x^(3)+y^(3)+z^(3)=3(a^(3)+b^(3))`
View Solutionसिद्ध कीजिए कि `1+omega^(n)+omega^(2n)=0`, यदि n एक धनात्मक पूर्णांक है जो 3 का गुणांक नहीं है ।
View Solutionसिद्ध कीजिए कि `sqrt(-1-sqrt(-1-sqrt(1- . .. . . . oo)))` तक `=omega` या `omega^(2)`
View Solutionयदि `x+(1)/(x)=1` तो सिद्ध कीजिए कि `x^(2000)+(1)/(x^(2000))=-1`
View Solutionयदि `x^(2)+x+1=0` तो सिद्ध कीजिए कि -
`(x+(1)/(x))^(2)+(x^(2)+(1)/(x^(2)))^(2)+ . . .+(x^(27)+(1)/(x^(27)))^(2)=54`
View Solutionसिद्ध कीजिए कि `(a+bomega+comega^(2))^(3)+(1+bomega^(2)+comega)^(3)=(2a-b-c)(2b-c-a)(2c-a-b)`
View Solutionयदि `omega=-(1)/(2)+(sqrt(3))/(2)i` तो सिद्ध कीजिए कि `omega^(3)=1`
View Solutionनिम्न सम्मिश्र संख्याओं का संयुग्मी ज्ञात कीजिए ।
(i) `3-2i` (ii) `(1)/(3+4i)`
View Solution`(isqrt(-9)+7i)/(1+i)` का संयुग्मी ज्ञात कीजिए ।
View Solutionनिम्नलिखित सम्मिश्र संख्याओं `x+iy` को के रूप में निरूपित कीजिए ।
(i) `(2-sqrt(-25))/(1-sqrt(-16))` (ii) `(5+2i)/(-1+sqrt(3i))`
(iii) `(sqrt(5)-7i)(sqrt(5)-7i)^(2)+(-2+7i)^(2)`
View Solutionनिम्नलिखित सम्मिश्र संख्याओं का मापांक ज्ञात कीजिए ।
(i) `1+sqrt(3)i` (ii) `sqrt(3)+i` (iii) `(1+i)/(1+sqrt(3)i)`
View Solutionयदि `z_(1)=2-i,z_(2)=1+i`, तब `|{:(z_(1)+z_(2)+1)/(z_(1)-z_(2)+i):}|` का मान ज्ञात कीजिए ।
View Solutionयदि `alpha` तथा `beta` सम्मिश्र संख्याएं है तथा `|beta|=1`, तब सिद्ध कीजिए `|{:(beta-alpha)/(1-bar(alpha)beta):}|=1`
View Solutionनिम्नलिखित संख्याओं को ध्रुवीय रूप (polar form) में निरूपित कीजिए ।
(i) `(1+7i)/((2-i)^2)` (ii) `(1+2i)/(1-3i)`
View Solutionनिम्न सम्मिश्र संख्याओं को ध्रुवीय रूप में लिखो ।
(i) `2(cos30^(@)+isin30^(@))xx3(cos90^(@)+ i sin90^(@))` (ii) `(cos150^(@)+ i sin150^(@))/(cos60^(@)+isin60^(@))`
View Solutionसिद्ध कीजिए कि -
(i) `{:[((3-2i)/(2-5i))+((3-2i)/(2+5i))]:}`, एक परिमेय संख्या है
(ii) `{:[((2+3i)/(3+4i))((2-3i)/(3-4i))]:}`, एक वास्तविक संख्या है ।
View Solutionयदि `sqrt(a+ib)=x+iy` तो सिद्ध कीजिए कि `sqrt(a-ib)=x-iy`
View Solutionसिद्ध कीजिए -
`sqrt(a+ib)+sqrt(a-ib)=sqrt(2(sqrt(a^(2)+b^(2))+a))`
View Solutionयदि `x+iy=sqrt((a+ib)/(x+id))`, तो सिद्ध कीजिए कि
View Solutionयदि `root(3)(a+ib)=x+iy`, तो सिद्ध करें की
`a/x+b/y=4(x^(2)-y^(2))`
View Solutionसिद्ध कीजिए कि x का एक वास्तविक मान समीकरण `(1-ix)/(1+ix)`= a-ib का हल है यदि
View Solutionदिखाइए कि सम्मिश्र संख्याओं (3+2i), (2-i) तथा (-7i) को निरूपित करने वाले बिंदु समरेखीय है ।
View Solutionसमद्विबाहु समकोणीय त्रिभुज (C पर समकोण) से शीर्षो A,B,C द्वारा क्रमशः सम्मिश्र संख्याएँ `z_(1),z_(2),z_(3)` निरूपित है सिद्ध कीजिए कि
`(z_(1)-z_(2))^(2)=2(z_(1)-z_(3))(z_(3)-z_(2))`
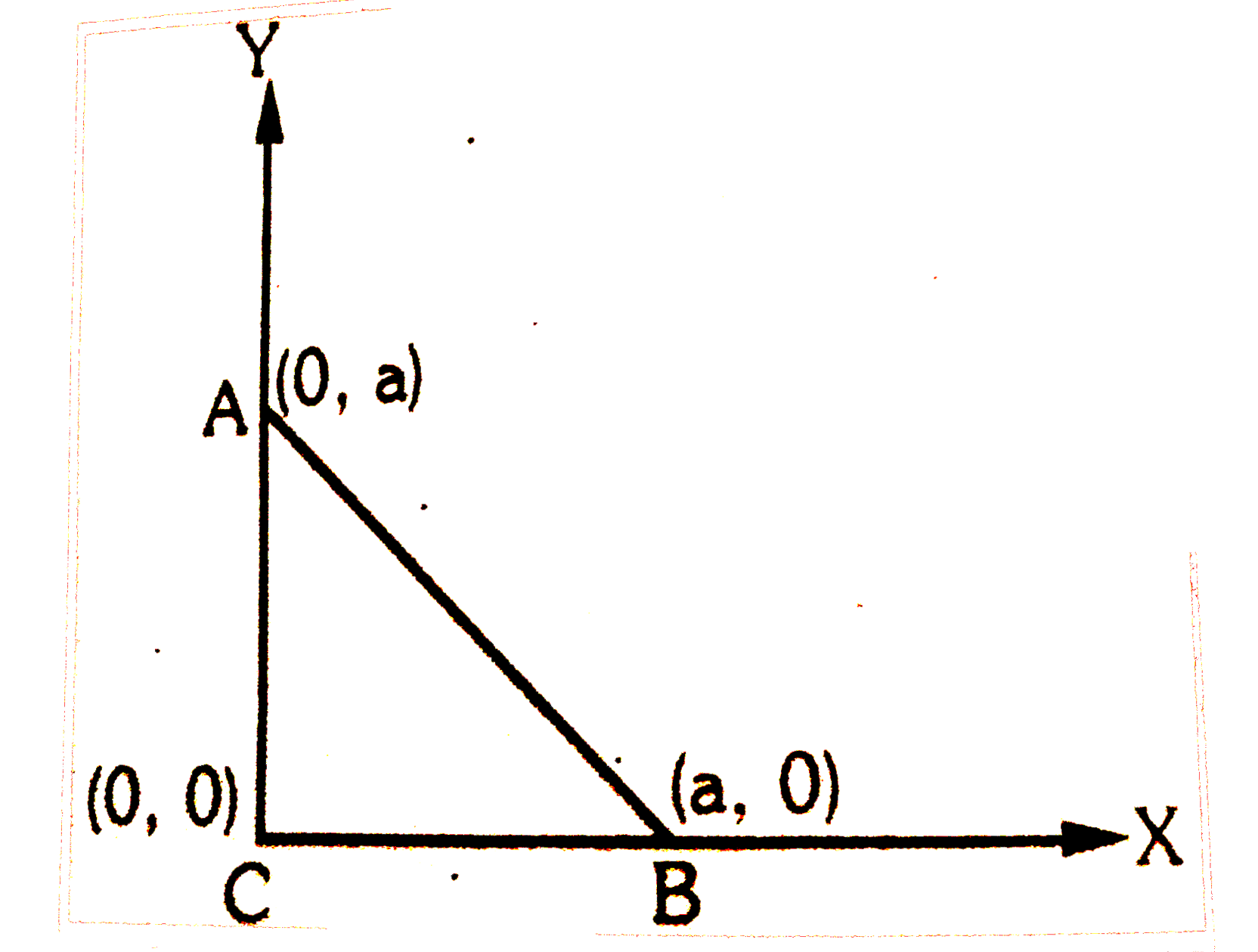
View Solutionयदि `((1+i)x-2i)/(3+i)+((2-3i)y+i)/(3-i)=i` तो x व y के मान ज्ञात कीजिए ।
View Solutionयदि `alpha,beta,gamma` किसी वास्तविक संख्या p के घनमूल है अशून्य x,y,z के लिए `(xalpha+ybeta+zgamma)/(xbeta+ygamma+zalpha)` का मान ज्ञात कीजिए ।
View Solutionयदि `|z_(1)|=|z_(2)|= . . .=|z_(n)|=1`, तो सिद्ध कीजिए कि -
`|z_(1)+z_(2)+ . . . +z_(n)|=|(1)/(z_(1))+(1)/(z_(2))+ . . . +(1)/(z_(n))|`
View Solutionसम्मिश्र संख्या `z_(1)=z^(2)-z,z=cos theta+i sintheta` का मापांक तथा कोणांक ज्ञात कीजिए
View Solutionयदि n एक विषम पूर्णांक है जो 3 से बड़ा है तथा 3 का गुणांक नहीं है तब सिद्ध कीजिए कि `x^(3)+x^(2)+x,(x+1)^(n)-x^(n)-1` का एक गुणनखण्ड है ।
View Solutionयदि n एक विषम संख्या है जो 3 का गुणांक नहीं है तो सिद्ध कीजिए कि
`f(x,y)=(x+y)^(n)-x^(n)-y^(n),xy(x+y)(x^(2)+xy+y^(2))` से विभाजित है |
View Solutionz के लिए हल कीजिए । `|z|+z=(2+i)`
View Solutionयदि `(a+ib)=sqrt((1+i)/(1-i))`, तब सिद्ध कीजिए कि `a^(2)+b^(2)=1`
View Solution`((1)/(1-2i)+(3)/(1+i))((3+4i)/(2-4i))` को `a+ib` के रूप में लिखिए ।
View Solution`z inC`, के लिए निम्नलिखित को सिद्ध कीजिए -
(i) `(1)/(2)(z+bar(z))=` वास्तविक `(z)` (ii) `(1)/(2i)(z-bar(z))=` अधिकल्पित `(z)`
View Solution
उदाहरण questions and complete solutions for chapter सम्मिश्र संख्याएँ of SHREE BALAJI MATHS (HINDI) of Class 11