Complete Solutions to BITSAT Archives of chapter WAVE MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVE MOTION |
| BITSAT GUIDE | BITSAT Archives |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
The equation of a simple harmonic motion is given by `y = 3 sin.(pi)/(2) (50 t-x)`, where x and y are in metres and t is in seconds, the ratio of maximum particle velocity to the wave velocity is
View SolutionA stretched string of length 2 m vibrates in 4 segments. The distance between consecutive nodes is
View SolutionAt t=0, a transverse wave pulse in a wire is described by the function `y=6//(x^(2)-3)` where x and y are in metres. The function y(x,t) that describes this wave equation if it is travelling in the positive x direction with a speed of `4.5 m//s` is
View Solutionin a sine wave ,postive of different particles at time t=0 is shown in figure. The equation for this wave if it is travelling along postive x -axis can beB
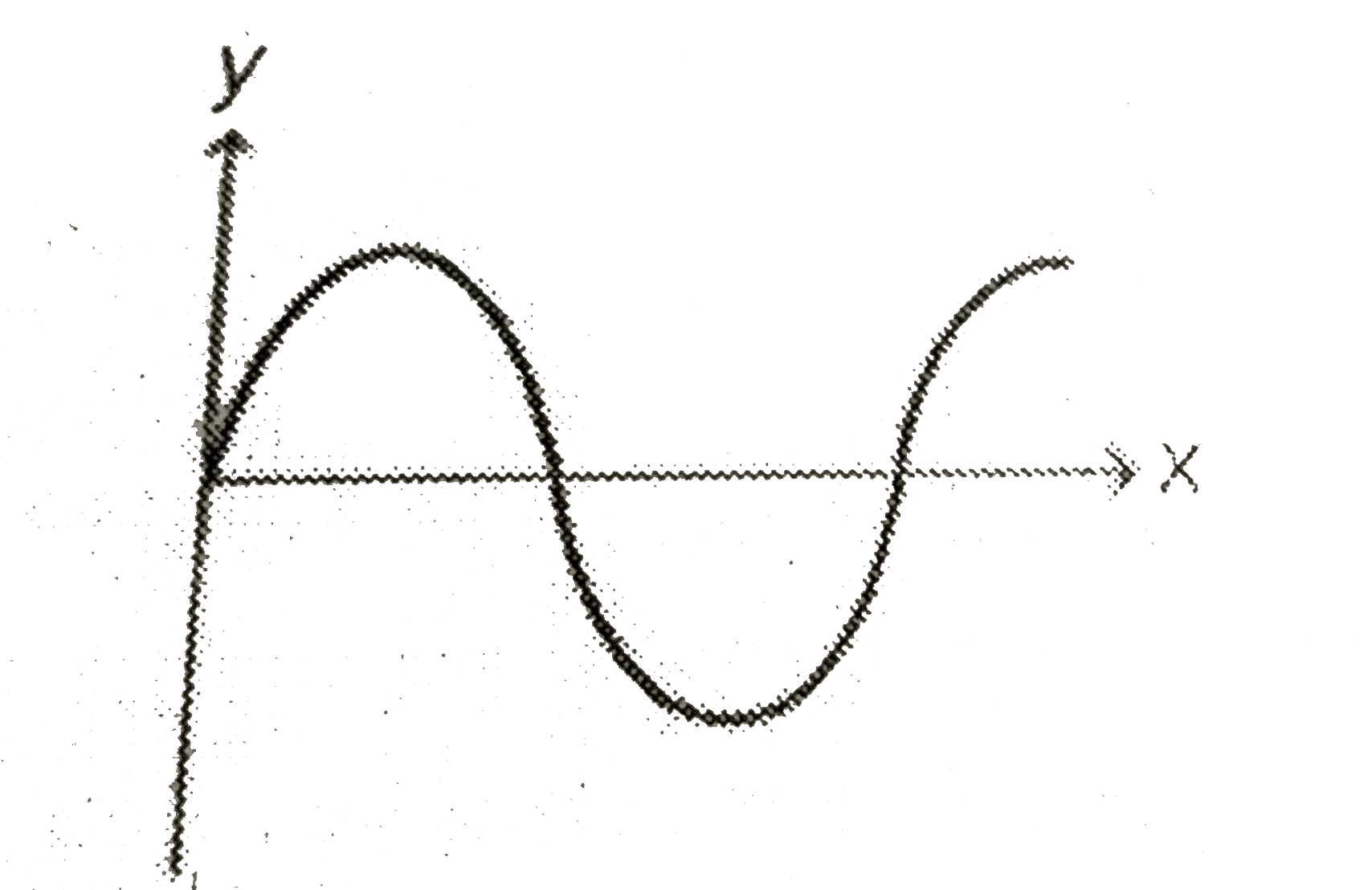
View SolutionA wave has velocity u in medium P and velocity 2 u in medium Q . If the wave is incident in medium P at an angle of `30^(@)` then the angle of refraction will be
View SolutionThe equation of progressive wave is `y = 0.2 sin 2pi``[(t)/(0.01)-(x)/(0.3)]`, where x and y are in metre and t is in second. The velocity of propagation of the wave is
View SolutionTwo progressive waves having equation `x_(1) = 3 sin omegatau` and `x_(2) = 4 sin (omegatau + 90^(@))` are superimposed. The amplitude of the resultant wave is
View SolutionA particle on the trough of a wave at any instant will come to the mean position after a time ( T = time period)
View Solution
BITSAT Archives questions and complete solutions for chapter WAVE MOTION of BITSAT GUIDE PHYSICS (HINGLISH) of Class 11