Complete Solutions to Practice Exercise of chapter WAVE MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVE MOTION |
| BITSAT GUIDE | Practice Exercise |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
The equation of a wave travelling on a stretched string along the x-axis is `y = ae^(-(bx+ct))`. The direction of propagation of wave is
View SolutionIn (Q. 1.) the maximum displacement of particle of string is
View SolutionIn (Q. 1.) the speed of wave is
View SolutionThe wave travels along a string whose equation is `y=(p^(3))/(p^(2)+(px-qt)^(2))`, where p = 2 unit and q = 0.5 units.
Find the direction of propagation of wave.
View SolutionIf wave y = A cos `(omegat + kx)` is moving along x-axis The shape of pulse at t = 0 and t = 2 s
View SolutionAt any instant a wave travelling along the string shown in figure. Here, point A is moving upward. Which of the following statement is true?

View SolutionIn the given figure,

View SolutionIf a wave propagates through a medium. Then, the velocity of particle of medium is given by
View SolutionIn a wave motion `y = sin (kx - omega t),y` can represent :-
View SolutionThe equation of a wave travelling on a stretched string is y = 4 sin `2 pi ((t)/(0.02)-(x)/(100))`
Here, x and y are in cm and t is in second. The speed of wave is
View SolutionIn (Q. 10.) the ratio of particle velocity amplitude and wavelength is
View SolutionIn (Q. 10.) the relative deformation amplitude of medium is
View SolutionAlong a stretched string equation of transverse wave is `y = 3 sin [2pi ((x)/(20)-(t)/(0.01))]`
Where, x, y are in cm and t is in second. Calculate wave velocity.
View SolutionA transverse wave along a string is given by
`y = 2 sin (2pi (3t - x) + (pi)/(4))`
where x and y are in cm and t in second. Find acceleration of a particle located at x = 4 cm at t = 1s.
View SolutionA travelling wave is described by the equation `y = y_(0) sin ((ft - (x)/lambda))`. The maximum particle velocity is equal to four times the wave velocity if
View SolutionAlong a stretched wire a transverse wave passes with speed 3000 m/s. If the tension in the wire increased four times, then the velocity of the wave is
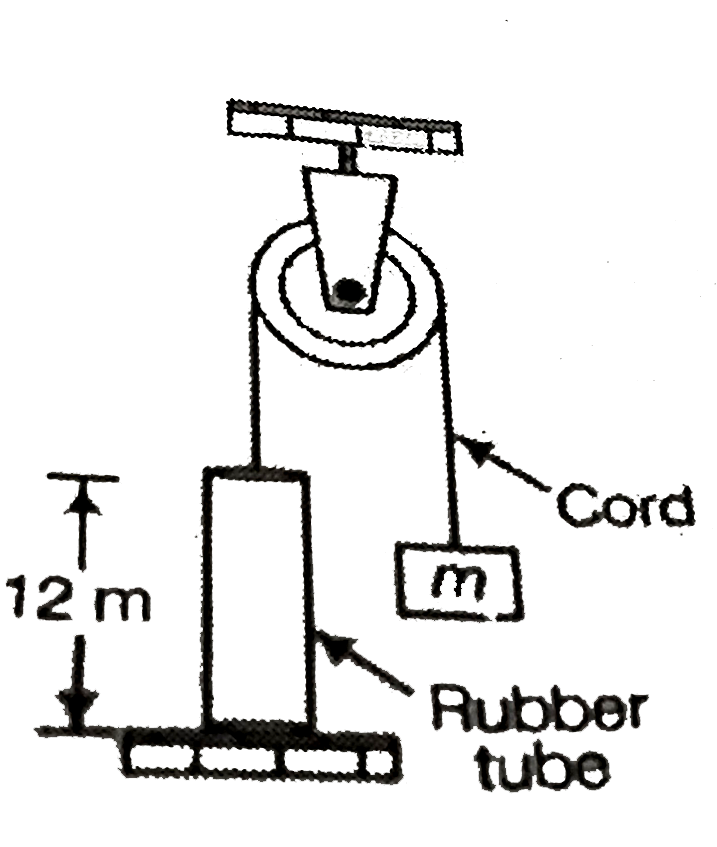
View SolutionA long rubber tube having mass 0.9 kg is fastened to a fixed support and the free end of the tube is attached to a cord which passes over a pulley and supports an object, with a mass of 5 kg as shown in figure. If the tube is struck by a transverse blow at one end, find the time required for the pulse to reach the other end.
View SolutionThe time taken by a transverse wave going on a wire having mass 5 g, form one end to another end of wire is 0.5 s. The area of cross-section fo wire is `1 mm^(2)` and Young's modulus of elasticity is `16 xx 10^(11) N//m^(2)`. The speed of wave is 80 m/s. The strain in wire is
View SolutionFind the time taken by a transverse wave to travel the full length fo a uniform rope of mass 0.1 kg and length 2.45 m hangs from the ceiling
View SolutionA transverse wave of equation y = 2 sin `(0.01 x +30 t)` moves on a stretched string from one end to another end. In the equation of wave, x and y are in cm and t is in second. The time taken by wave to reach from one end to another end of string is 5 s. The length of string is
View SolutionA sinusoidal wave travelling in the same direction have amplitudes of 3 cm and 4 cm and difference in phase by `pi//2`. The resultant amplitude of the superimposed wave is
View SolutionTwo simple harmonic motions are represented by the equations `y_(1) = 10 sin (3pit + (pi)/(4))`
and `y_(2) = 5 (3 sin 3 pi t+sqrt(3) cos 3 pi t)`. Their amplitudes are in the ratio of
View SolutionPredict for the wave `y = A cos.(2pix)/(lambda) sin ((2pivt)/(lambda))`
View SolutionA string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 2 mm. The amplitude of a particle at distance `l//8` from the fixed end is
View SolutionIn (Q. 24.) the tension in string is T and the linear mass density of string is `mu`. The ratio of magnitude of maximum velocity of particle and the magnitude of maximum acceleration is
View SolutionIn (Q. 24.) if at t = 0, y = 2.5 mm, the equation of standing wave is
View SolutionIf a string fixed at both ends vibrates in four loops. The wavelength is 10 cm. The length of string is
View SolutionIn (Q. 27.) the distance of plucking poing from the fixed end is
View SolutionA stretched wire carries a body of density `sigma = 8000 kg//m^(3)` at its end. The fundamental frequency of vibration of wire is 280 Hz. The body is dipped completely in a vessel of water. Find the new frequency of fundamental mode of vibrations. (Density of water is `rho = 1000 kg//m^(3)`)
View SolutionAn elastic string of length 2 m is fixed at its end. The string starts to vibrate in third overtone with a frequency 1200 Hz. The ratio of frequency of lower overtone and fundamental is
View SolutionIf a string is stretched with a weight 4 kg then the fundamental frequency is equal to 256 Hz. What weight is needed to produce its octave?
View SolutionA string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm` and `16 cm` respectively. The minimum possible length of the string is:
View SolutionA sonometer wire of length 114 cm is fixed at both the ends. Where should the two bridges be placed so as to divide the wire into three segments whose fundamental frequencies are in the ratio `1 : 3 : 4`?
View SolutionA wave of angular frequency `omega` propagates so that a certain phase of oscillation moves along x-axis, y-axis, z-axis with speeds `c_(1) c_(2)` and `c_(3)` respectively.
View SolutionWave of frequency 500 Hz has a phase velocity `360 m//s`. The phase difference between two displacement at a certain point at time `10^(-3)s` apart will be
View SolutionEquation of a plane wave is given by `4 sin .(pi)/(4)[2t+(x)/(8)]`. The phase difference at any given instant of two particles 16 cm apart is
View SolutionThe transverse displacement `y(x, t)` of a wave on a string is given by `y(x, t)= e ^(-(ax^(2) + bt^(2) + 2sqrt((ab))xt)`. This represents a :
View SolutionFor a wave y = 0.0002 sin `[2pi (110 t -(x)/(3))+(pi)/(3)]`
is travelling in a medium. Find energy per unit volume being transferred by wave if density of medium is `1.5 kg//m^(3)`.
View Solution
Practice Exercise questions and complete solutions for chapter WAVE MOTION of BITSAT GUIDE PHYSICS (HINGLISH) of Class 11