Complete Solutions to Single Correct Answer Type of chapter SUPERPOSITION AND STANDING WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SUPERPOSITION AND STANDING WAVES |
| CENGAGE PHYSICS DPP | Single Correct Answer Type |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
Two sources of sound `A` and `B` produces the wave of `350 Hz`. They vibrate in the same phase. The particel `P` is vibrating under the influence of these two waves, if the amplitudes at the point P produced by the two waves is `0.3mm` and `0.4mm` then the resultant amplitude of the point `P` will be when `AP-BP=25cm` and the velocity of sound is `350m//sec`.
View SolutionTwo waves are propagating to the point P along a straight line produced by two sources A and B of simple harmonic and of equal frequency. The amplitude of every wave at P is `a` and the phase of A is ahead by `pi//3` than that of B and the distance AP is greater than BP by `50 cm`. Then the resultant amplitude at the point P will be if the wavelength `1` meter
View SolutionThe minimum intensity of sound is zero at a point due to two sources of nearly equal frequencies when
View SolutionOut of given four waves (1),(2),(3) and (4)
`y=asin(kx+omegat)` .(1)
`y=asin(omegat-kx)` ..(2)
`y=acos(kx+omegat)` ..(3)
`y=acos(omegat-kx)` .(4)
emitted by four different source `S_1`,`S_2`,`S_3` and `S_4` respectively, interference phenomena would be observed in space under appropriate conditions when
View SolutionEquation of motion in the same direction is given by `y_(1) =A sin (omega t - kx), y_(2) = A sin ( omega t - kx- theta )`. The amplitude of the medium particle will be
View SolutionThe amplitude of a wave represented by displacement equation `y=(1)/(sqrta)sinomega+-(1)/(sqrtb)cosomegat` will be
View SolutionTwo waves having equaitons
`x_1=asin(omegat+phi_1)`,`x=asin(omega+phi_2)`
If in the resultant wave the frequency and amplitude remain equal to those of superimposing waves. Then phase difference between them is
View SolutionA travelling wave `y=Asin(kx-omegat+theta)` passes from a heavier string to a lighter string. The reflected wave has amplitude `0.5A`. The junction of the string is at `x=0` The equation of the reflected is :
View SolutionThe figure shown at time `t = 0` second, a rectangular and triangular pulse on a uniform wire are approcaching other. The pulse speed is `0.5 cm//s` . The resultant pulse at `t = 2` second is

View SolutionIn a large room, a person receives direct sound waves froma source 120 metres away from him. He also receives waves from the same source which reach him, being reflected from the 25 metre high ceiling at a point halfway between them. The two waves interfere constuctively for wavelength of
View SolutionTwo speakers connected to the same source of fixed frequency are placed 2.0m apart in a box. A sensitive microphone placed at a distance of 4.0 m from their midpoint along the perpendicular bisector shows maximum response. The box is slowly rotated until the speakers are in line with the microphone. The distance between the midpoint of the speakers and the microphone remains unchanged. Exactly five maximum responses are observed in the microphone in doing this. the wavelength of the sound wave is
View Solution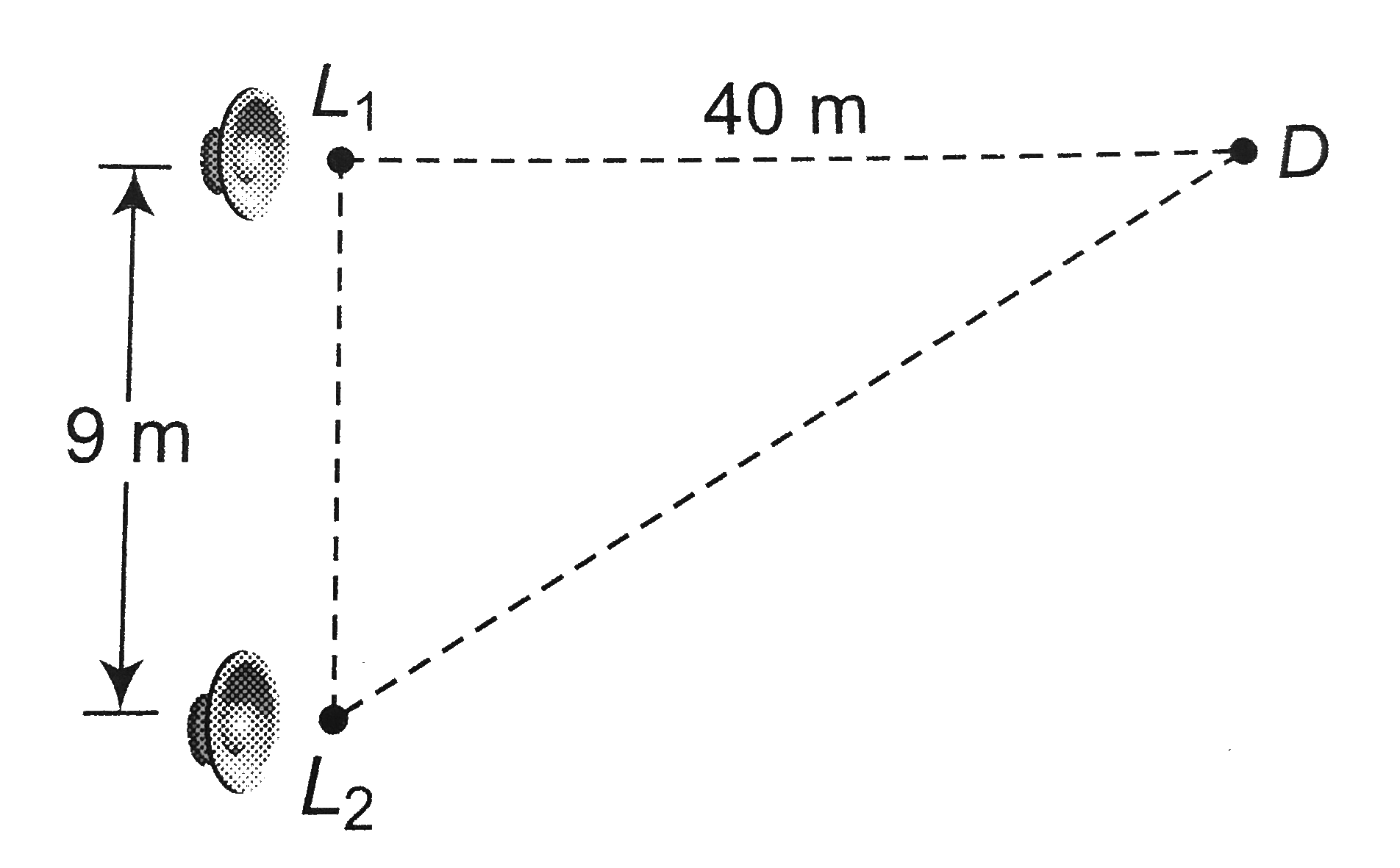
Two loudspeakers `L_1` and `L_2` driven by a common oscillator and amplifier, are arranged as shown. The frequency of the oscillator is gradually increased from zero and the detector at D records a series of maxima and minima. If the speed of sound is `330ms^-1` then the frequency at which the first maximum is observed is
View SolutionTwo pulses travel in mutually opposite directions in a string with a speed of `2.5 cm//s` as shown in the figure. Initially the pulses are `10 cm` apart. What will be the state of the string after two seconds?
View SolutionAn unknown frequency `x` produces 8 beats per seconds with a freuquency of `250` Hz and 12 beats with `270Hz`. Source then `x` is
View SolutionTwo tuning forks when sounded together produced `4beats//sec`. The frequency of one fork is 256. The number of beats heard increases when the fork of frequency 256 is loaded with wax. The frequency of the other fork is
View SolutionIf two tuning fork A and B are sounded together they produce 4 beats per second. A is then slightly loaded with wax, they produce 2 beats when sounded again. The frequency of A is 256. The frequency of B will be
View SolutionThe frequencies of two sound sources are 256 Hz and 260 Hz, At `t=0` the intesinty of sound is maximum. Then the phase difference at the time `t=1//16` sec will be
View SolutionWhen a tuning fork of frequency 341 is sounded with another tuning fork, six beats per second are heard. When the second tuning fork is loaded with wax and sounded with the first fork, the number of beats is two per second. The natural frequency of the second tuning fork is
View SolutionTuning fork `F_1` has a frequency of 256 Hz and it is observed to produce `6 beats//second` with another tuning fork `F_2`. When `F_2` is loaded with wax, it still produces `6 beats//sec` with `F_1`. The frequency of `F_2` before loading was
View SolutionBeats are produced by two waves given by `y_(1)= a sin 2000 pi t` and `y_(2) =a sin 2008 pi t `. The number of beats heard per second is
View SolutionA tunig fork whose frequency as given by mufacturer is `512 Hz` is being tested with an accurate oscillator it is found that the fork produces a beat of 2 Hz when oscillator reads 514 Hz but produces a beat of 6 Hz when oscillator reads 510 Hz. The actual frequency of fork is
View SolutionTen tuning forks are arranged in increasing order of frequency is such a way that any two nearest tuning forks produce `4 beast//sec`. The highest freqeuncy is twice of the lowest. Possible highest and the lowest frequencies are
View SolutionTwo identical flutes produce fundamental notes of frequency `300Hz` at `27^@C`. If the temperature of air in one flute is increased to `31^@C`, the number of the beats heard per second will be
View SolutionThe freuquency of tuning forks A and B are respectively `3%` more and `2%` less than the frequency of tuning fork `C`. When A and B are simultaneously excited, 5 beats per second are produced. Then the frequency of the tuning fork `A` (in Hz)` Is
View SolutionTwo tuning forks have frequencies 380 and 384 Hz respectively. When they are sounded together they
produce 4 beats. After hearing the maximum sound how long will it take to hear the minimum sound
View SolutionWhen a tuning fork A of unknown frequency is sounded with another tuning fork B of frequency 256Hz, then 3 beats per second are observed. After that A is loaded with wax and sounded, the again 3 beats per second are observed. The frequency of the tuning fork A is
View SolutionIn a stationary wave all the particles
View SolutionWhen a stationary wave is formed, then its frequency is
View SolutionAt a certain instant a stationary transverse wave is found to have maximum kinetic energy. The appearance of string at that instant is
View SolutionWhich two of the given transverse waves will give stationary wave when get superimposed?
`z_(1) = a cos (kx-omegat) " "(A)`
`z_(2) = a cos (kx +omegat) " "(B)`
`z_(3) = a cos (ky - omegat) " "(C )`
View SolutionFor the stationary wave `y=4sin((pix)/(15))cos(96pit)`, the distance between a node and the next antinode is
View SolutionA wave is represented by the equation `y = a sin(kx + omega t)` is superimposed with another wave to form a stationary wave such that the point x = 0 is a node. Then the equation of other wave is :-
View SolutionTwo waves are approaching each other with a velocity of `20m//s` and frequency `n`. The distance between two consecutive nodes is
View SolutionTwo sinusoidal waves with same wavelengths and amplitudes travel in opposite directions along a string with a speed `10ms^-1`. If the minimum time interval between two instant when the string is flat is `0.5s`, the wavelength of the waves is
View SolutionConsider the three waves `z_(1), z_(2) "and" z_(3)` as
`z_(1) = A "sin"(kx - omega t)`
`z_(2) = A "sin"(kx + omega t)`
`z_(3) = A "sin"(ky - omega t)`
Which of the following represents a standing wave?
View SolutionSpacing between two successive nodes in a standing wave on a string is `x`. If frequency of the standing wave is kept unchanged but tension in the string is doubled, then new sapcing between successive nodes will become:
View SolutionA standing wave pattern is formed on a string One of the waves if given by equation `y_1=acos(omegat-kx+(pi)/(3))` then the equation of the other wave such that at `x=0` a node is formed is
View SolutionA tuning fork vibrating with a sonometer having 20 cm wire produces 5 beats per second. The beat frequency does not change if the length of the wire is changed to 21 cm. The frequency of the tuning fork (in Hertz) must be
View SolutionIn order to double the frequnecy of the fundamental note emitted by a stratched string the length is reduced to `3/4` th of the original length and the tension is changed. The factor by which the tension is to be changed is
View SolutionA string of 7m length has a mass of `0.035 kg.` If tension in the string is `60.N,` then speed of a wave on the string is
View Solutionbetween two rigid support. The point where the string has to be pluked and touched are
View SolutionTwo wires are fixed in a sonometer. Their tensions are in the ratio 8:1. The lengths are in the ratio 36:35. The diameter are in the ratio 4:1 Densities of the materials are in the ratio 1:2 If the lower frequency in the setting is 360 Hz. The beat frequency when the two wires are sounded together is
View SolutionA string is rigidly tied at two ends and its equation of vibration is given by `y=cos 2pix.` Then minimum length of string is
View SolutionFundamental frequency of sonometer wire is n. If the length, tension and diameter of wire are tripled the new fundamental frequency is
View SolutionA string of length 2 m is fixed at both ends. If this string vibrates in its fourth normal mode with a frequency of 500 Hz. Then the waves would travel on it with a velocity of
View SolutionThe length of two open organ pipes are `l` and `(l+deltal)` respectively. Neglecting end correction, the frequency of beats between them will b approximately.
View SolutionTwo closed organ pipes, when sounded simultaneously gave 4 beats per sec. If longer pipe has a length of 1 m. Then length of shorter pipe will be (v=300 m//s`
View SolutionA closed organ pipe and an open organ pipe are tuned to the same fundamental frequency. The ratio of their lengths is
View SolutionOn producing the waves of frequency 1000 Hz in a kundt's tube the total distance between 6 successive nodes n 85 cm. Speed of sound in the gas filled in the tude is
View SolutionWhat is the base frequency if a pipe gives notes of frequencies 425, 255 and 595 and decide whether it is closed at one end or open at both ends?
View SolutionTwo closed organ pipes of length 100 cm and 101 cm 16 beats is 20 sec. When each pipe is sounded in its fundamental mode calculate the velocity of sound `
View SolutionIn a resonance pipe the first and second resonance are obtained at depths 22.7 cm and 70.2 respectively. What will be the end correction?
View SolutionA tuning fork of frequency `340 H_(Z)` is sounded above an organ pipe of length `120 cm` . Water is now slowly poured in it . The minimum height of water column required for resonance is ( speed of sound in air = `340 m//s`)
View SolutionAn organ pipe is closed at one end has fundamental frequency of 1500 Hz. The maximum number of overtones generated by this pipe which a normal person can hear is
View SolutionThe fundamental of a closed pipe is 220 Hz. If `(1)/(4)` of the pipe is filled with water, the frequency of the first overtone of the pipe now is
View SolutionA glass tube `1.5 m` long and open at both ends, is immersed vertically in a water tank completely. A tuning fork of 660 Hz is vibrated and kept at the upper end of the tube and the tube is gradually raised out of water the total number of resonances heard before the tube comes out of water taking velocity of sound air `330m//s` is
View Solution
Single Correct Answer Type questions and complete solutions for chapter SUPERPOSITION AND STANDING WAVES of CENGAGE PHYSICS (HINGLISH) of Class 11