Complete Solutions to Exercises of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| CP SINGH | Exercises |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Select the correct statements.
(i) A simple harmonic motion is necessarily periodic
(ii) A simple harmonic motion is necessarily oscillatory
(iii) An oscillatory motion is necessarily periodic
(iv) A periodic motion is necessarily oscillatory05:54View SolutionA student says that he had applied a force `F=-ksqrtx` on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle
04:06View SolutionWhich of the following quantities are always negative in a simple harmonic motion?
02:58View SolutionWhich of the followign quantities are always zero in a simple harmonic motion?
02:10View SolutionThe time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
04:04View SolutionThe average acceleration in one tiome period in a simple harmonic motion is
02:07View SolutionA partilce is executive simple harmonic motion given by
`x=5sin(4t-pi/6)`
The velocity of the particle when its displacement is 3 units is01:51View SolutionA particle starts SHM from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of the maximum speed, its displacement y is
02:10View SolutionA body of mass `5g` is executing SHM with amplitude `10cm`, its velocity is `100cm//s`. Its velocity will be `50cm//s` at a displacement from the mean position equal to
02:29View SolutionA particle is vibrating in SHM. If its velocities are `v_1` and `v_2` when the displacements from the mean postion are `y_1` and `y_2`, respectively, then its time period is
04:00View SolutionThe phase (at a time t) of a particle in simple harmonic motion tells
01:49View SolutionWhich of the following equation does not represent a simple harmonic motion
03:10View SolutionWhich of the following is a simple harmonic motion
View SolutionThe equation of SHM of a particle is `(d^2y)/(dt^2)+ky=0`, where k is a positive constant. The time period of motion is
01:10View SolutionA particle is executing SHM. Then the graph of acceleration as a function of displacement is
01:08View SolutionA particle is executing SHM. Then the graph of velocity as a function of displacement is
01:15View SolutionFor a simple pendulum the graph between length and time period will be
01:14View SolutionOut of the following function reporesenting motion of a particle which represent `SHM`
(i) ` y = sin omega t - cos omega t `
(ii) `y = sin^(3) omega t`
(iii)`y =5cos ((3pi)/(4) - 3omega t)`
(iv) ` y = 1+ omega t + omega^(2) t^(2) `03:00View SolutionA particle excuting `S.H.M.` of amplitude `4 cm `and `T = 4` sec .The time take by it to move position extreme position to half the amplitude is
02:30View SolutionA particle is executing SHM of amplitude `4cm` and time period `12s`. The time taken by the particle in going from its mean position to a position of displacement equal to `2cm` is `T_1`. The time taken from this displaced position to reach the extreme position on the same side is `T_2.T_1//T_2` is
03:08View SolutionA simple harmonic oscillation has an amplitude `A` and time period `T`. The time required to travel from `x = A` to ` x= (A)/(2)` is
03:05View SolutionTime period of a particle executing `SHM` is `8` sec. At `t=0` it is at the mean position. The ratio of the distance covered by the particle in the `1st` second to the `2nd` second is:
03:06View SolutionTwo particles P and Q start from origin and execute simple harmonic motion along X-axis with same amplitude but with periods `3s` and `6s` respectively. The ratio of the velocities of P and Q when they meet is
02:18View SolutionA particle executes simple harmonic motion with a period of `16s`. At time `t=2s`, the particle crosses the mean position while at `t=4s`, its velocity is `4ms^-1` amplitude of motion in metre is
05:15View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of `t=4//3s` is
 02:24View Solution
02:24View SolutionIf x, and a denote the displacement, the velocity and the acceler of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
01:03View SolutionWhich one of the following equation at the repressents simple harmonic motion ?
02:09View SolutionThe potential energy of a particle with displacement X is `U(X)`. The motion is simple harmonic, when (K is a positive constant)
05:02View SolutionThe kinetic energy and potential energy of a particle executing simple harmonic motion will be equal, when displacement (amplitude `=a`) is
02:05View SolutionThe angular velocity and amplitude of simple pendulum are `omega` and r respectively. At a displacement x from the mean position, if its kinetic energy is T and potential energy is U, find the ration of T to U.
01:36View SolutionA verticle mass-spring system executed simple harmonic ascillation with a period `2s` quantity of this system which exhibits simple harmonic motion with a period of `1sec` are
07:12View SolutionA particle executes simple harmonic motion with a frequency. (f). The frequency with which its kinetic energy oscillates is.
02:20View SolutionWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is
02:07View SolutionThere is a body having mass `m` and performing `SHM` amplitude a There is a restoring force `F = - Kx` where `x` is the displacement The total energy of body depends upon
01:44View SolutionA body is executing simple harmonic motion. At a displacement `x` its potential energy is `E_(1)` and at a displacement `y` its potential energy is `E_(2)` The potential energy `E` at displacement `(x+y)` is
01:51View SolutionStarting from the origin a body osillates simple harmonicall with a period of 2 s. A fter what time will its kinetic energy be 75% of the total energy?
03:10View SolutionIf a simple harmonic oscillator has got a displacement of `0.02m` and acceleration equal to `2.0ms^-2` at any time, the angular frequency of the oscillator is equal to
01:10View SolutionA point simple harmonic oscilation of the period and the equation of motion is given by `x a sin (omega t + pi //6)` after the step of friction of the time period the velocity of the part will be equal to half of its maximum velocity?
02:42View SolutionTwo simple harmonic are represented by the equation `y_(1)=0.1 sin (100pi+(pi)/3) and y_(2)=0.1 cos pit`.
The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is.03:04View SolutionThe time period of simple pendulum is T. If its length is increased by 2%, the new time period becomes
02:11View SolutionThe length of a simple pendulum is increased by 44%. The percentage increase in its time period will be
02:14View SolutionA simple pendulum is oscillating in a lift. If the lift starts moving upwards with a uniform acceleration, the period will
01:47View SolutionA girl is swinging on a swing in the sitting position. How will the period of swing be affected if she stands up?
01:50View SolutionA metallic sphere is filled with water and hung by a long thread. It is made to oscillate. If there is a small hole in the bottom through which water slowly flows out, the time period will
04:19View SolutionA simple pendulum suspended from the ceiling of a trans has a time period `T` when the train is at rest. If the train is accelerating uniformly at `a` then its time period
03:34View SolutionA simple pendulum is set up in a trolley which moves to the right with an acceleration a on a horizontal plane. Then the thread of the pendulum in the mean position makes an angle `theta` with the vertical
02:46View SolutionA simple pendulum of length `l` is suspended from the celing of a cart which is sliding without friction on as inclined plane of inclination theta . What will be the time period of the pendulum?
02:59View SolutionThe length of a second's pendulum on the surface of the moon, where g is `1//6^(th)` if the value of g on the surface of the
02:05View SolutionA pendulum clock is taken `1km` inside the earth from mean sea level. Then the pendulum clock
03:42View SolutionA pendulum clock, which keeps correct time at sea level, loses `15s` per day when taken to the top of a mountain. If the radius of the earth is `6400km`, the height of the mountain is
05:30View SolutionThe mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this plenet. If it is a 2 second's pendulum on earth?
03:49View SolutionA second's pendulum is placed in a space laboratory orbiting around the earth at a height `3R`, where R is the radius of the earth. The time period of the pendulum is
01:12View SolutionFor a particle executing `S.H.M.,` the kinetic energy `K` is given `K = K_(0) cos ^(2)omega t`. The maximum value of potential energy is:
02:46View SolutionA linear harmonic oscillator of force constant `2 xx 106Nm^(-1)` and amplitude `0.01m` has a total mechanical energy `160 J`. Among the followinhg statement , which are correct?
i Maximum `PE`is `100J`
ii Maximum `KE`is `100J`
iii Maximum `PE` is `160J`
iv Maximum `PE` is zero03:12View SolutionThe total mechanicla energy of a spring mass sytem in simple harmonic motion is `E=1/2momega^2 A^2`. Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude `A` remains the same. The new mechanical energy will
03:29View SolutionThe average energy in one time period in simple harmonic motion is
01:14View SolutionIn a simple harmonic motion
05:54View SolutionIn a simple harmonic motion
(i) the maximum potential energy equal the maximum kinetic energy
(ii) the minimum potential energy equals the minimum kinetic energy
(iii) the minimum potential energy equals the maximum kinetic energy
(iv) the maximum potential energy equals the minimum kinetic energy01:44View SolutionA mass m attached to a spring oscillates with a period of `3s`. If the mass is increased by `1kg` the period increases by `1s`. The initial mass m is
02:06View SolutionA mass `M` is suspended from a massless spring. An additional mass `m` stretches the spring further by a distance `x`. The combined mass will oscillate with a period
02:50View SolutionA mass suspended on a vertical spring oscillates with a period of `0.5s`. When the mass is allowed to hang at rest, the spring is stretched by
02:18View SolutionA pan with a set of weights is attached to a light spring. The period of vertical oscillations is `0.5s`. When some additional weights are put in pan, the period of oscillations increases by `0.1s`. The extension caused by the additional weights is
04:32View SolutionThe two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be
 01:33View Solution
01:33View SolutionThe two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be
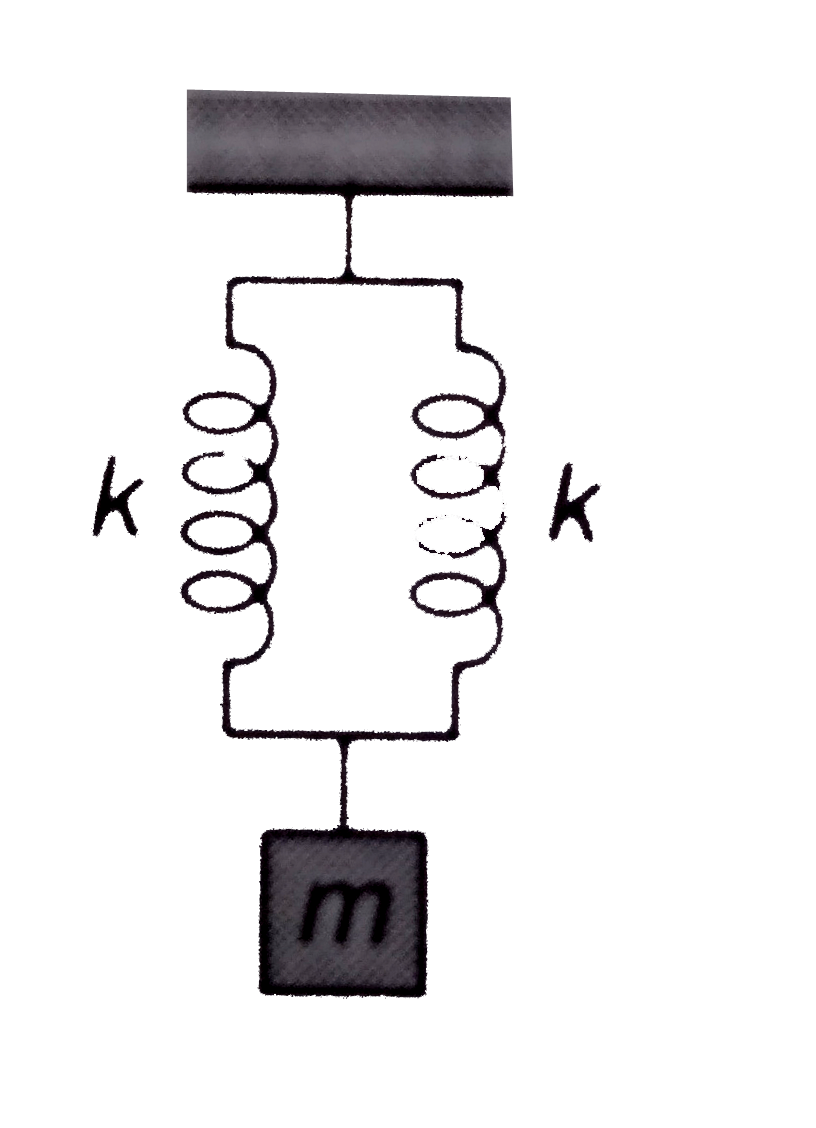 01:26View Solution
01:26View SolutionThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
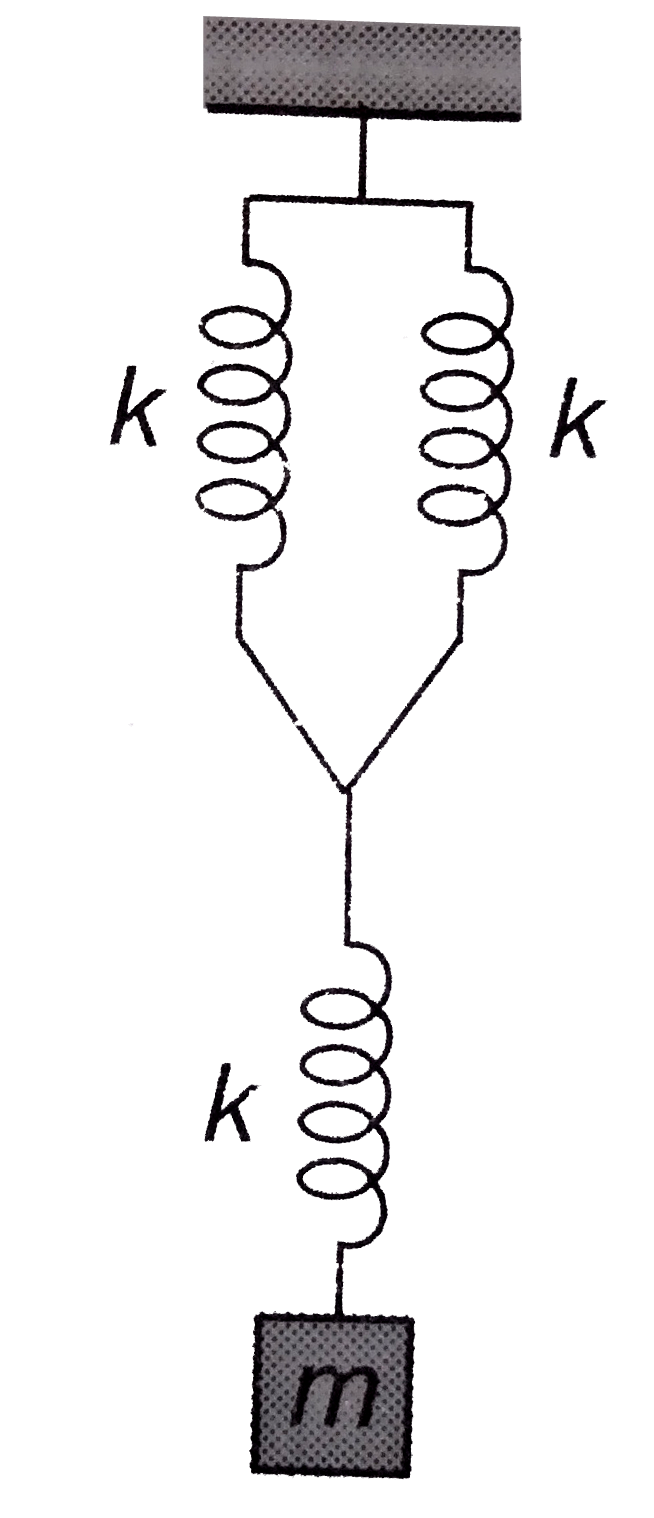 01:33View Solution
01:33View SolutionWhen a body is suspended from two light springs separately, the periods of vertical oscillations are `T_1` and `T_2`. When the same body is suspended from the two spring connected in series, the period will be
03:42View SolutionIn previous problem, if the body is suspended from the two springs connected in parallel, the time period will be
04:24View SolutionTwo bodies (M) and (N) of equal masses are suspended from two separate massless springs of spring constants (k_1) and (k_2) respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of (M) to the of (N) is.
02:10View SolutionSprings of constants k, 2k, 4k, 8k,…….,2048k are connected in series. A mass m is attached to one end and the system is allowed to oscillate. The time period is approximately
04:20View SolutionA spring mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will
02:51View SolutionA massless spring, having force constant k, oscillates with frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass `2m` is suspended from one half. The frequency of oscillation will now be
03:03View SolutionTwo blocks of masses `m_1` and `m_2` are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block `(m_2)` drops off. The other block `(m_1)` will
 02:43View Solution
02:43View SolutionIn previous question, the amplitude of vibration is
03:20View SolutionAs shown in figure in a simple harmonic motion oscillator having identical four springs has time period
 02:45View Solution
02:45View SolutionA person normally weighing `60 kg` stands on a platform which oscillates up and down harmonically at a frequency `2.0 sec^(-1)` and an amplitude `5.0 cm` . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, `Take g = 10 m//sec^(2)`.
05:10View SolutionA body is on a rough horizontal surface which is moving horizontally in SHM of frequency `2Hz`. The coefficient of static friction between the body and the surface is `0.5`. The maximum value of the amplitude for which the body will not slip along the surface is approximately
03:46View SolutionA coin is placed on a horizontal platform, which undergoes horizontal simple harmonic motion about a mean position O. The coin does not slip on the platform. The force of friction acting on the coin is F.
(i) F is always directed towards O
(ii) F is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
(iii) `F=0` when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
(iv) F is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motion03:23View SolutionIn the previous question, the angular frequency of the simple harmonic motion is `omega`. The coefficient of friction between the coin and the platform is `mu`. The amplitude of oscillation is gradually increased. The coin will begin to slip on the platform for the first time
(i) at the extreme positions of oscillations
(ii) at the mean position
(iii) for an amplitude of `(mug)/(omega^2)`
(iv) for an amplitude of `(g)/(muomega^2)`05:25View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency `omega`. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
03:41View SolutionA mass of `2.0 kg` is put on a flat pan attached to a vertical spring fixed on the ground as shown in figure. The mass of the spring and the pan is negligible. When pressed slightly and realeased the mass executes a simple contant is `200 N//m`. What should be the minimum amplitude of the motion, so that the mass gets the detached from the pan? `(Take g= 10 m//s^(2))`
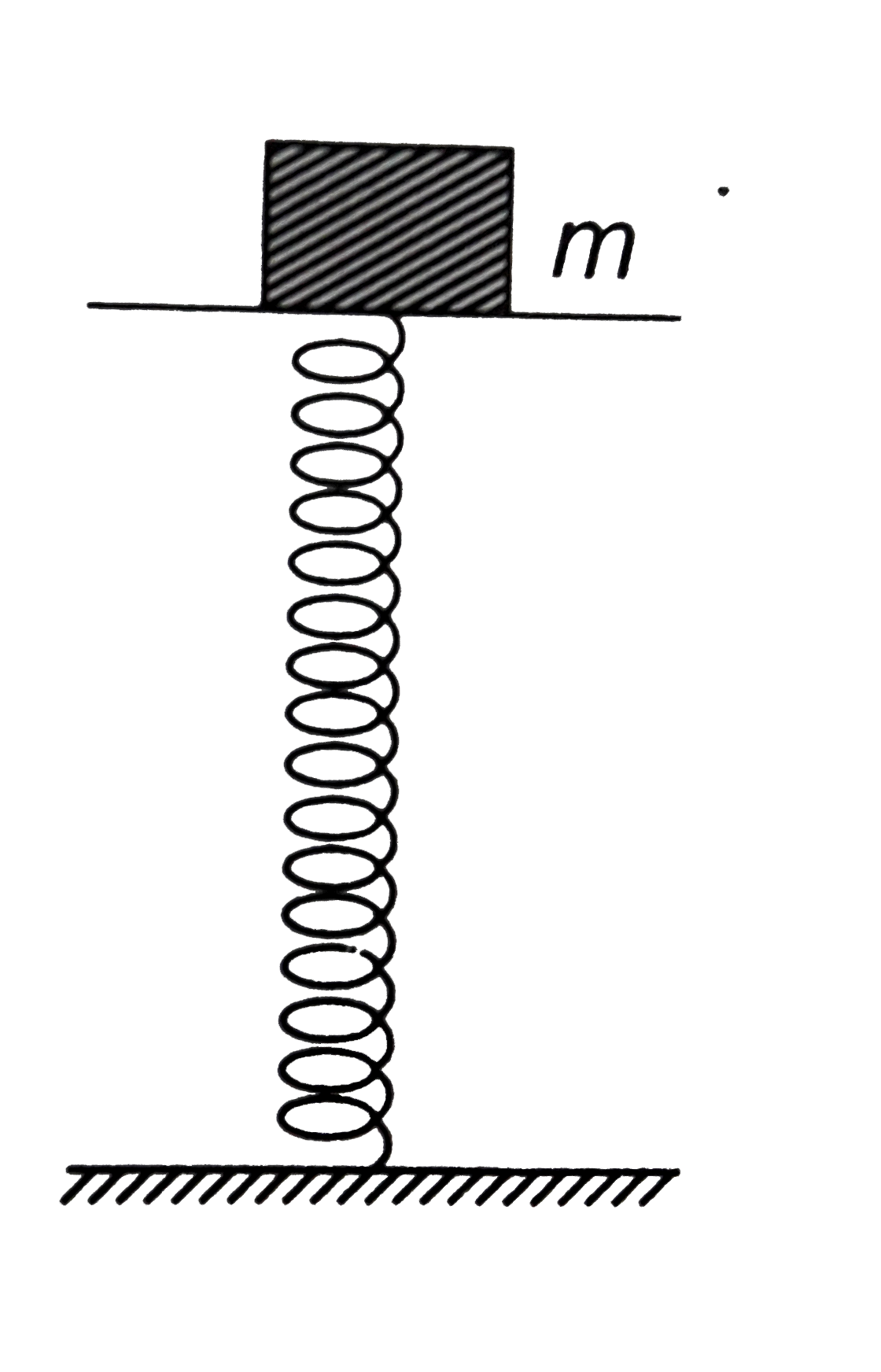 03:18View Solution
03:18View SolutionA mass (M), attached to a horizontal spring, executes S.H.M. whith amplitude `A_(1). When the mass (M) passes throgh its mean position then shaller mass (m) is placed over it and both of them move together with amplitude `A_(2). The ration of.
04:20View SolutionA uniform rod of length `L` and mass `M` is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. `k`. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle `theta` in one direction and released. the frequency of oscilllation is-
 03:36View Solution
03:36View SolutionIn the figure, the vertical sections of the string are long. A is released from rest from the position shown. Then
 View Solution
View SolutionIf a hole is bored along a diameter of the earth and a stone is dipped into the hole, it will
View SolutionA hole is bored along a diameter of the earth and a particle is dropped into it. If R is the radius of the earth and g is the acceleration due to gravity at the surface of the earth, then the time period of oscillation of the particle is
View SolutionA particle moves in x-y plane according to rule `x=asin omegat` and `y=-acosomegat`. The particle follows
01:23View SolutionThe motion of a particle is given by `x=A sin omegat+Bcos omegat`. The motion of the particle is
02:24View SolutionA particle moves on the X-axis according to the equation `x=A+Bsinomegat`. Let motion is simple harmonic with amplitude
01:13View SolutionThe ratio of the amplitudes of the simple harmonic oscillations given by `y_1=Asinomegat` and
02:14View SolutionThe minimum phase difference between the two simple harmonic oscillations `y_1=1/2sinomegat+(sqrt3/2) cos omegat` and `y_2=sinomegat+cosomegat` is
03:54View SolutionA body executes SHM of period `3s` under the influence of one force, and SHM of period `4s` under the influence of a second force. When both the forces act simultaneously in the same direction, the period of oscillation will be
03:26View SolutionThe displacement of a particle is given by `r=A(haticosomegat+hatjsinomegat)`. The motion of the particle is
01:30View SolutionElectrons in an oscilloscope are deflected by two mutually perpendicular oscillating electric field such that at any time the displacement due to them are given by `x=Acosomegat`, `y=Asin(omegat+pi/6)`. Then the path of the electron is
03:59View SolutionTwo particles A and B execute simple harmonic motions of period T and `5T//4`. They start from mean position. The phase difference between them when the particle A complete an oscillation will be
03:30View SolutionTwo simple pendulum of length `5m` and `20m` respectively are given small displacement in one direction at the same time. They will again be in the same phase when the pendulum of shorter length has completed oscillation.
01:38View SolutionTwo simple pandulum whose lengths are `100cm` and `121cm` are suspended side by side. Then bobs are pulled together and then released. After how many minimum oscillations of the longer pendulum will two be in phase again. ?
04:03View SolutionTwo particles execute SHM of the same time period along the same straight lines. They cross each other at the mean position while going in opposite directions. Their phase difference is
01:48View SolutionTwo pendulum of lengths `1m` and `16m` are in phase at the mean position at a certain instant of time. If T is the time period of the shorter pendulum, then the minimum time after which they will again be in phase is
03:41View SolutionTime period of is simple pendulum of length `L` is `T_(1)` and the point time peirod of a uniform rod of the same length `L` pivotal about one end and oscillating in vertical plane is `T_(2)`. Amplitude of oscillation in both the cased is small. The `T_(1)//T_(2)` is:
02:33View SolutionA disc of radius `R` and mass `M` is plvoted at the rim and is set for small oscillation. if simple pendlum has to have the same period as that the of the disc, the length of the simple pendlum should to
02:08View Solution
Exercises questions and complete solutions for chapter SIMPLE HARMONIC MOTION of CP SINGH PHYSICS (HINGLISH) of Class 11
