Complete Solutions to Examples of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| CP SINGH | Examples |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
A particle executes `SHMx=Asin(omegat+phi)`. At `t=0`, the position of the particle is `x=(sqrt3A)/(2)` and it moves along the positive x-direction. Find
(a) phase constant `phi`
(b) velocity at `t=pi/omega`
(c) acceleration at `t=pi/omega`04:59View Solution(a) A particle executes simple harmonnic motion with an amplitude of `10cm`. At what distance from the mean position are the kinetic and potential energies equal?
(b) The maximum speed and acceleration of a particle executing simple harmonic motion are `10m//s` and `50cm//s`. Find the position(s) of the particle when the speed is `8cm//s`.06:09View SolutionThe equation of motion of a particle started at `t=0` is given by `x=5sin(20t+pi//3)` where x is in centimeter and t in second. When does particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?03:21View SolutionConsider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.
02:47View SolutionA particle executing simple harmonic motion has angular frequence `6.28s^-1` and amplityude 10 cm. Find a the time period, b the maximum speed c. the maximum acceleration d. the speed when thedisplacement is 6 cm from the mean position e. the speed t `t=1/6s` assuming that the motion starts from rest t t=0.
11:29View SolutionA point particle of mass `0.1kg` is executing SHM of amplitude `0.1m`. When the particle passes through the mean position, its kinetic energy is `8xx10^-3J`. Obtain the equation of motion of this particle if the initial phase of oscillation is `45^@`.
03:25View SolutionTwo particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
02:04View SolutionA body makes angular simple harmonic motion of amplitude `pi//10rad` and time period `0.05s`. If the body is at a displacement `theta = pi//10 rad` at `t = 0`, write the equation giving angular displacement as a function of time.
01:23View SolutionA simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find a. the time period b. the linear amplitude of the bob, c. The speed of the bob when the strig makes 0.02 rad with the vertical and d. the angular acceleration when the bob is in moemntary rest. Take `g=10 ms^-2`.
09:30View SolutionA simple pendulum is taken at a place where its separation from the earth's surface is equal t the radius of the earth. Calculate the time period of small oscillations if the length of the string is 1.0m. Take `g=pi^2ms^-2` at the surface of the earth.
06:25View SolutionA particle suspended from a vetical spring oscillastes 10 times per sencon. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretche by 0.20 cm. Take `g=pi^2ms^-2`
09:34View Solution(a) The right block collides with left block and sticks to it. Find amplitude of the resulting SHM.

(b) The block starts from left wall and moves with constant speed v. All collisions are elastic. Find time period of periodic motion.
 06:54View Solution
06:54View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
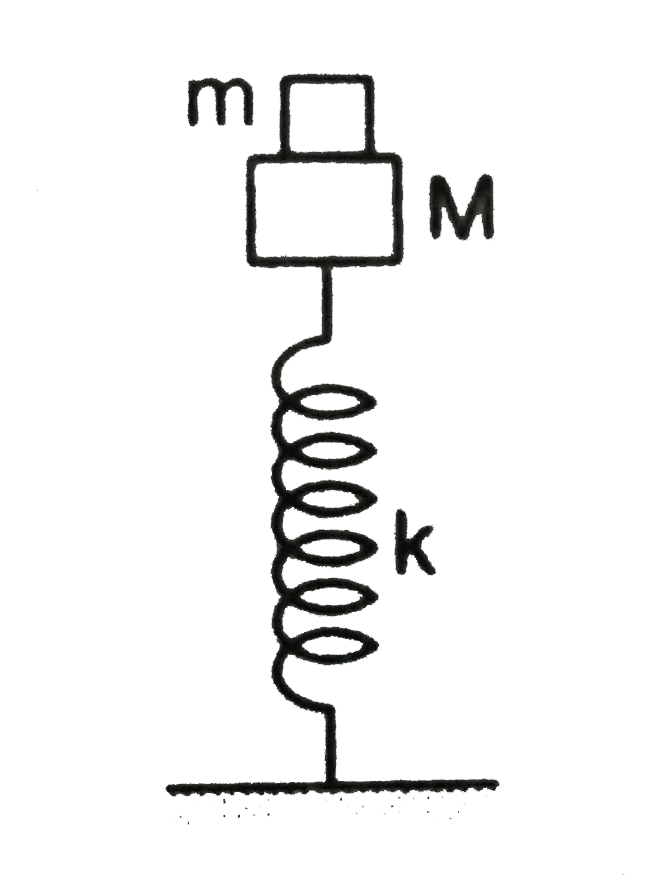 06:16View Solution
06:16View SolutionThe friction coeficeint betweenteh tow blocks shown in figure is `mu` and the horizontal plance is smooth. A. If the system is slightly diplaced and released find the time period. B. find the magnitude of the frictional force between the blocks when the displacement from the mean position is x. c. What can be the maximum amplitude if the upper block does not slip relative to the lower block?
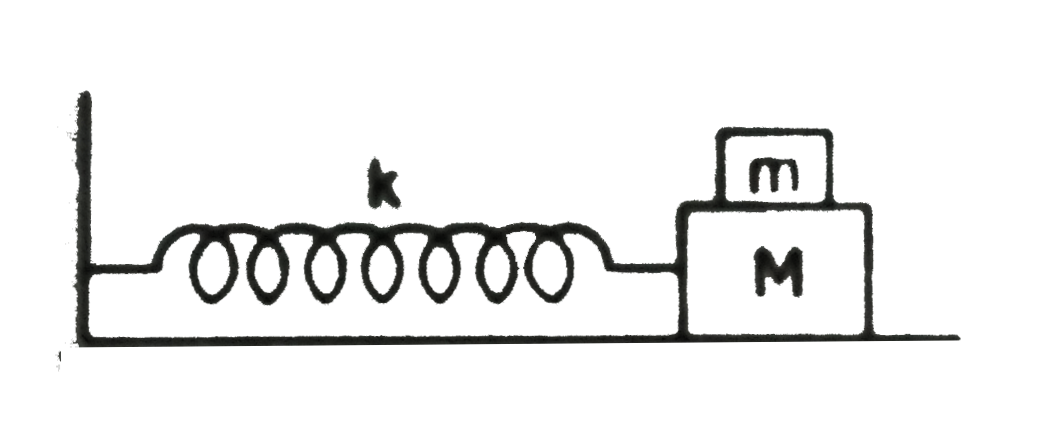 07:07View Solution
07:07View SolutionThe block of mass `m_1` shown in figure is fastened to the spring and the block of mass `m_2` is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance `(2/k)(m_1+m_2)gsintheta` against the spring and released. Find the position where the two blocks separate. c. What is the common speed of blocks at the time of separation?
 10:42View Solution
10:42View SolutionIn figure, `k = 100 N//m, M = 1kg` and `F = 10 N`

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of `2 m//s` to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?14:57View SolutionA particle of mass `m` is attached with three springs `A,B` and `C` of equal force constancts `k` as shown in figure. The particle is pushed slightly against the spring `C` and released. Find the time period of oscillation.
 . 04:59View Solution
. 04:59View SolutionA simple pendulum of length L and mass m has a spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.
 05:00View Solution
05:00View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.
 07:23View Solution
07:23View SolutionA horizontal spring block system of mass M executes simple harmonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
04:45View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.
 08:58View Solution
08:58View SolutionConsider the situation as shown. The pulley has a moment of inertia I, and radius r, the block is in equilibrium. Find the time period of mass m. Assume no slipping.
 06:09View Solution
06:09View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.
 11:19View Solution
11:19View SolutionThe spring as shown in figure is kept in a stretched position with extension `x` when the system is relesed. Assuming the horizontal surface to be frictionless, the frequency of oscillation is
 05:27View Solution
05:27View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
 04:43View Solution
04:43View SolutionFind the time period of small oscillations of the following systems.
(a) A uniform rod of mass m and length L is suspended through a pin hole at distance `L//4` from top as shown.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform disc of mass m and radius r suspended through a point `r//2` away from centre.
(d) A uniform square plate of edge a suspended through a corner.09:45View SolutionA uniform rod of length l is suspended by end and is made to undego small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
05:04View SolutionA uniform disc of radius r is to be suspended through a small hole made in te disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
09:31View SolutionA closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude `2^@` and time period 2s. Find a the radius of the circular wire. b. the speed of the particle farthest away from the point of suspension as it goes though its mean position c. the aceleration of this particle as ilt goes through its mean position and extreme position. Take `g=pi^2 sms^-2`
16:38View Solution(a) A uniform disc of radius `5*0cm` and mass `200g` is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period `0.20s`, find the torsional constant of the wire.
(b) In the previous part, another disc is placed over the first one and the time period of the system become `0.65`. Find the M.I. of the second disc about the wire.07:09View SolutionThe potential energy of a particle of mass m is given by `U(x)=U_0(1-cos cx)` where `U_0` and c are constants. Find the time period of small oscillations of the particle.
02:18View SolutionA small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation.
 02:47View Solution
02:47View SolutionAsume that as narrow tunnel is dug between two diametricaly opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that ilf a particle is relesed in this tunel, ilt wil execute a simple harmonic motion. Calculate the time period of this motion.
06:49View SolutionIn the previous problem, if tunnel is dug along a chord, find time period.
 05:58View Solution
05:58View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance `R//2` from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.View SolutionA uniform plate of mass M stays horizontally symmetrically on two wheels rotating in opposite directions. The separation between the wheels is L. the friction coefficient between each and the plate is `mu`. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.
 View Solution
View SolutionTwo simple harmonic motions are represented by the following equations
`y_1=10sinpi/4(12t+1)`
`y_2=5(sin 3pit+sqrt3cos3pit)`
Find out the ratio of their amplitudes. What are the time periods of two motions?04:06View Solution(a) A particle is subjected to two SHMs of same time period in the same direction. If `A_1=6cm`, `A_2=8cm`, find the resultant amplitude if the phase difference between the motions is (a) `0^@`, (b) `60^@`, (c) `90^@` and (d) `120^@`.
(b) In the previous problem if `A_1=A_2=a` and resultant amplitude is also a, find phase difference between them.
(c) Three SHMs of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is `120^@` ahead of first and the phase of the third motion is `120^@` ahead of the second. Find the amplitude of the resultant motion.08:02View Solution(a) A particle is subjected to two simple harmonic motions
`x_1=A_1sin omegat` and `x_2=A_2 sin (omegat+pi//3)`.
Find (i) the displacement at `t=0`, (ii) the maximum speed of the particle and (iii) the maximum acceleration of the particle.
(b) A particle is subjected to two simple harmonic motions, one along the x-axis and the other on a line making an angle of `45^@` with the x-axis. The two motions are given by
`xy=x_0sinomegat` and `s=s_0sin omegat`
Find the amplitude of the resultant motion.08:32View SolutionTwo linear SHM of equal amplitudes `A` and frequencies `omega` and `2omega` are impressed on a particle along `x` and `y - axes` respectively. If the initial phase difference between them is `pi//2`. Find the resultant path followed by the particle.
01:51View Solution
Examples questions and complete solutions for chapter SIMPLE HARMONIC MOTION of CP SINGH PHYSICS (HINGLISH) of Class 11
