Complete Solutions to EXAMPLE of chapter TEMPERATURE AND THERMAL EXPANSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | TEMPERATURE AND THERMAL EXPANSION |
| CP SINGH | EXAMPLE |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
A railway track (made of iron) is laid in winter when the average temperature is `18^@C`. The track consists of sections of 12.2 m placed one after the other. How much gap should be left between two such sections so that there in no compression during summer when the maximum temperature goes to `48^@C`? Coefficient of linear expansion of iron `= 11 xx 10^(-5 @)C^(-1)`.
02:17View SolutionAn iron rod and a copper rod lie side by side. As the temperature is changed, the difference in the lengths of the rods remains constant at a value of `10cm` . Find the lengths at `0^(@)C` . Coefficient of linear expansion of iron and copper are `1.1xx10^(-5)//^(@)C` and `1.7xx10^(-5)//^(@)C` respectively.
06:27View SolutionAn iron rod of length `50cm` is joined at an end to an aluminium rod of length `100cm` . All measurements refer to `20^(@)C` . Find the length of the composite system at `100^(@)C` and its average coefficient of linear expansion. The coefficient of linear expansion of iron and aluminium are `12xx10^(-6)//^(@)C` and `24xx10^(-6)//^(@)C` respectively.
06:35View Solution(a) A pendulum clock consists of an iron rod connected to a small, heavy bob. If it is designed to keep correct time at `20^(@)C` , how fast or slow will it go in 24 hours at `50^(@)C` ? `alpha_(iron)=1.2xx10^(-5)//^(@)C` .
(b) A pendulum clock having copper rod keeps correct time at `20^(@)C` . It gains 15 seconds per day if cooled to `0^(@)C` . Find the coefficient the of linear expansion of copper.09:39View SolutionA uniform steel wire of cross-sectional area `0.20mm^(2) ` is held fixed by clamping its two ends. If wire is cooled from `100^(@)C` to `0^(@)C` , find
(a) temperature strain
(b) temperature stress
(c) extra force exerted by each clamp on the wire. Young's modulus of steel `=2xx10^(11)N//m^(2)` , coefficient of linear expansion of steel `=1.2xx10^(-5)//^(@)C` .05:15View SolutionA steel wire `AB` of length `85cm` at `10^(@)C` is fixed rigidly at points `A` and `B` in an aluminium frame as shown. If the temperature of the system is raised to `110^(@)C` , what extra stress will be produced in the wire relative to aluminium frame. Assume that coefficient of linear expansion for aluminium and steel are `23xx10^(-6)//^(@)C` and `11xx10^(-6)//^(@)C` respectively and Young's moduls for steel is `2xx10^(11)` pa.
 05:04View Solution
05:04View Solution(a) The brass scale of a barometer gives correct reading at `0^(@)C` . Coefficient of linear expansion of brass is `2.0xx10^(-5)//^(@)C` . The barometer reads `75cm` at `27^(@)C` . What is the atmospheric pressure at `27^(@)C` ?
(b) A barometer reads `75.0cm` on a steel scale. The room temperature is `30^(@)C` . The scale is correctly graduated for `0^(@)C ` . The coefficient of linear expansion of steel is `alpha=1.2xx10^(-5)//^(@)C` and the coefficient of volume expansion of mercury is `gamma=1.8xx10^(-4)//^(@)C` . Find the correct atmospheric pressure.08:46View SolutionTwo metal strips, each of length `l` and thickness `d` at temperature `T_(0)` are riveted together so that their ends coincide. One strip is made of metal `A` having a linear coefficient `alpha_(B)` where `alpha_(A)gtalpha_(B)` . When this bimetallic-strip is heated to a temperature `(T_(0)+DeltaT)` , one strip becomes longer than the other and the bimetallic strip bends into an arc of a circle. What is the radius of curvature `R` of the strip ?
10:41View SolutionA piece of metal weighs 46 g in air and 30 g in lipuid of density `1.24 xx 10^3 kg m^(-3)` kept at `27^0C`. When the temperature of the liquid is raised to `42^0C` the metal piece weights 30.5 g . The density of the liqued at `42^0 C` is `1.20 xx 10^3 kg m^(-3)`. Calculate the coefficient of linear expandsion of the metal.
08:47View SolutionA sphete of deamrter 7.0 cm and mass 266.5 g float in a bath of liquid. As the temperature is raised, the sphere begins to sink at a temperature of `35^@ C`. If the density of liqued is `1.527 g cm^(-3)` at` 0^@C`, find the coeffiecient of cubical expamsion of the liquid. Neglect the expansion of the sphere.
05:02View SolutionA 1-L flask contains some mercury. It is found that at different temperature, the volume of air inside the flask remains the same. What is the volume of mercury in the flask, given that the coefficient of linear expansion of glass`=9xx10^(-6)//^(@)C` and the coefficient of volume expansion of `Hg=1.8xx10^(-4)//^(@)C` ?
04:25View SolutionA glass flask of volume one litre at `0^(@)C` is filled level full of mercury at this temperature. The flask and mercury are now heating to `100^(@)C` . How much mercury will spill out if coefficient of volume expansion of mercury is `1.2xx10^(-4)//^(@)C` and linear expansion of glass is `1.0xx10^(-4)//^(@)C` respectively ?
05:12View SolutionA piece of metal floats on mercury. The coefficients of volume expansion of the metal and mercury are `gamma_1` and `gamma_2` respectively. If the temperatures of both mercury and the metal are increased by an amount `DeltaT`, the fraction of the volume of the metal submerged in mercury changes by the factor............
07:36View SolutionA cubical block of co-efficient of linear expansion `alpha_s` is submerged partially inside a liquid of co-efficient of volume expansion `gamma_l`. On increasing the temperature of the system by `DeltaT`, the height of the cube inside the liquid remains unchanged. Find the relation between `alpha_s and gamma_l`.
07:22View SolutionA long mercury glass tube with a uniform capillary bore has in it a thread of mercury which is `1m` long at `0^(@)C` . What will be its length at `100^(@)C` if the real coefficient of expansion of mercury is `0.000182` and coefficient of cubical expansion of glass equal to `0.000025` ?
08:07View Solutiona glass tube of length `133cm` and of uniform cross-section is to be filled with mercury so that the volume of the unoccupied by mercury remains the same at all temperatures. If cubical coefficient for glass and mercury are respectively `0.000026//^(@)C` and `0.000182//^(@)C` , calculate the length of mercury column.
04:15View SolutionA glass tube of length `l_(0)` and of uniform cross-section is to be filled with mercury so that the length of the tube unoccoupied by mercury remains same at all temperatures. If `gamma_(g)=3alpha` , calculate length of mercury column.
11:29View SolutionAn aluminium cube of side `20cm` floats in mercury. How much farther will the block sink when tempereture rises from `27^(@)C` to `77^(@)C` ? Density of aluminium and mercury at `27^(@)C` are `2.7` and `13.6g//cc` while the coeficient of volume expansion of mercury and linear expansion of aluminium are `1.8xx10^(-4)//^(@)C` and `23xx10^(-6)//^(@)C` respectively.
10:37View SolutionA `U`-tube is filled with mercury. When two limbs are maintained at temperatures of `0^(@)C` and `100^(@)C` , then heights of the two columns are `100cm` and `101.8cm` . What is the real coefficient of cubical expansion of mercury ? (Expansion of vessel may be neglected)
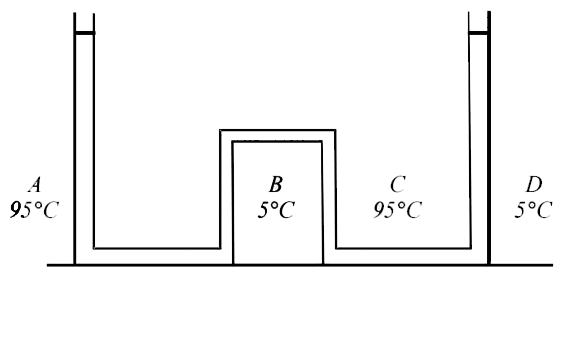
05:26View SolutionThe apparatus shown in the figure consists of four glass columns connected by horizontal section. The height of two central column B and C are 49 cm each. The two outer columns A and D are open to the temperature. A and C are maintained at a temperature of `95^@C` while the columns B and D are maintained at `5^@C`. The height of the liquid in A and D measured from the base the are 52.8 cm and 51cm respectively. Determine the coefficient of thermal expansion of the liquid
 08:32View Solution
08:32View Solution
EXAMPLE questions and complete solutions for chapter TEMPERATURE AND THERMAL EXPANSION of CP SINGH PHYSICS (HINGLISH) of Class 11
