Complete Solutions to EXERCISES of chapter TEMPERATURE AND THERMAL EXPANSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | TEMPERATURE AND THERMAL EXPANSION |
| CP SINGH | EXERCISES |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
View SolutionIf the temperature of a partient is `40^(@)C` , his temperature on the Fahrenheit scale will be
View SolutionThe reading of Centigrade thermometer coincides with that of Fahrenheit thermometer in a liquid. The temperature of the liquid is
View SolutionMaximum density of `H2O` is at the temperature
View SolutionAt what temperature the Fahrenheit and kelvin scales of temperature give the same reading ?
View SolutionIf a graph is plotted taking the temperature in Fahrenheit along the `Y`-axis and the corresponding temperature in Celsius along the `X`-axis, it will be a straight line
View SolutionWhich of the curves in figure represents the telation between Celsius and Fahrenheit temperatures? `
`
View Solutionwhich of the following pairs may give equal numerical values of the temperature of a boy?
View SolutionIn which of the following pairs of temperature scales, the size of a degree is idenital ?
(i) mercury scale and ideal gas scale
(ii) Celsius scale and mercury scale
(iii) Celsius scale and ideal gas scale
(iv) ideal gas scale and absolute scale
View SolutionA centigrade and a Fehrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fehrenheit thermometer registers `140^(@)C` . What is the fall in temperature as register by the centigrade thermometer
View SolutionOn a new scale of temperature (which is linear) and called the `W` scale. The freezing and boiling points of water are `39^(@)W` and `239^(@)W` respectively. What will be the temperature on the new scale, corresponding to a temperature of `39^(@)C` on the Celsius scale?
View SolutionWhat is the correct value of `0^(@) C` on the Kelvin scale?
View SolutionThe change in temperature of a body is `50^(@)C` . The change on the Kelvin scale is
View SolutionFor a constant volume gas thermometer, one should fill the gas at
View SolutionThe gas thermometer are more sensitive than the liquid thermometers because gases
View SolutionA temperature `T` is measured by a constant volume gas thermometer
(i) `T` is independent of the gas used at all pressure
(ii) `T` is independent of the gas used only at low pressure
(iii) The ideal gas scale agrees with the absolute scale of temperature
(iv) The ideal gas scale does not agrees with the absolute scale of temperature
View SolutionA constant volume gas thermopmeter shows pressure reading of `50cm` and `90cm` of mercury at `0^(@)C` and `100^(@)C` respectively. When the pressure reading is `60cm` of mercury, the temperature is
View SolutionA constant pressure air thermometer gave a reading of `47.5` units of volume when immersed in ice cold water, and 67 units in a boiling liquid. The boiling point of the liquid will be
View SolutionThe thermometer suitable for measuring a temperature of about `2000^(@)C` is
View SolutionThe temperature of the sun is measured with
View SolutionOn a thermometer, the freezing points of water is marked as `20^(@)C` and the boiling points of water is marked as `150^(@)C` . A temperature of `60^(@)C` will be read on this thermometer as
View SolutionA constant volume gas thermometer shows pressure reading of `50cm` and `90cm` of mercury at `0^(@)C` and `100^(@)C` , respectively. When the pressure reading is `70cm` of mercury, the temperature is
View SolutionThe ratio among coefficient of volume expansion, superficial expansion and linear expansion i.e.,
`gamma` . `beta` : `alpha` is
View SolutionAn iron tyre is to be fitted onto a wooden wheel 1.0 m in diameter. The diameter of the tyre is 6 mm smaller than that of wheel the tyre should be heated so that its temperature increases by a minimum of (coefficient of volume expansion of iron is `3.6xx10^-5//^@C`)
View SolutionTwo rods of length `l_(1)` and `l_(2)` are made of material whose coefficient of linear expansion are `alpha_(1)` and `alpha_(2)` , respectively. The difference between their lengths will be independent of temperatiure if `l_(1)//l_(2)` is to
View SolutionTwo rods , one of aluminium and the other made of steel, having initial length `l_(1)` and `l_(2)` are connected together to from a sinlge rod of length `l_(1)+l_(2)` . The coefficient of linear expansion for aluminium and steel are `alpha_(a)` and `alpha_(s)` for `AC` and `BC` . If the distance `DC` remains constant for small changes in temperature,
View SolutionThree rods of equal of length are joined to from an equilateral triangle ABC. `D` is the midpoint of AB. The coefficient of linear expansion is `alpha_(1)` for AB and `alpha_(2)` for `AC` and `BC` . If the distance `DC` remains constant for small changes in temperature,

View SolutionA steel scale measures the length of a copper wire as `80.0 cm` when both area at `20^(@)C` (the calibration temperature for scale). What would be the scale read for the length of the wire when both are at `40^(@)C`? (Given `alpha_("steel") = 11 xx 10^(-6) per ^(@)C` and `alpha_("copper") = 17 xx 10^(-6) per^(@)C`)
View SolutionA measuring tape amde of steel is calibrated at `5^(@)C` . If the coefficient of linear expansion of steel `10^(-5)//^(@)C` . If the coefficinet of linear expansion of steel `10^(-5)//^(@)C` , the percent error in measurement at `40^(@)C` is
View SolutionTwo indentical recrangular strips. One of copper and the other of steel, are rivetted together to from o bimetallic strip `(alpha_copper gtalpha_steel)`. On hearing. This strip will
View SolutionIf a bimetallic strip is heated it will
View SolutionA steel sheet at `20^(@)C` has the same surface area as a brass sheet at `10^(@)C` . If the coefficient of linear expansion of steel is `11xx10^(-6)//K` and that of bross is `19xx10^(-6)//K` , the common temperature at which both the sheets would have the same surface area is
View SolutionIf the pemperature of a uniform fod is slifhely increased by `Deltat` its mement of inertia I about o pqrpendicular bisector imcreases by
View SolutionIf the temperature of a uniform rod is slightly increased by `Deltat`, its moment of inertia I about a line parallel to itself will increased by
View SolutionWhen the temperature of a rod increases from t to `r+Delta t`, its moment of inertia increases from I to `I+Delta I`. If `alpha` is the value of `Delta I//I` is
View SolutionThe volume of a block of a metal changes by `012%` when it is heated through `20^(@)C` . The coefficient of linear expansion of the metal is
View SolutionA horizontal tube, open at both ends, contains a column of liquid. The length of this liquid column does not change with temperature. Let `gamma` : coefficient of volume expansion of the liquid and `alpha` : coefficient of linear expansion of the material of the tube
View SolutionA liquid with coefficient of volume expansion `gamma` is filled in a container of a material having coefficient of linear expansion `alpha` . If the liquid overflows on heating, then
View SolutionA flask is filled with mercury at temperature `28^(@)C` . If the flask and the contents are heated to `48^(@)C` , the volume of mercury above the mark will be `(alpha_(glass=9xx10^(-6)//^(@)C` , `gamma_(Hg)=180xx10^(-6)//^(@)C)`
View SolutionA one litre flask contains some mercury. It is found that at different temperatures the volume of air inside the flask remains the same. The volume of mercury in the flask is `(alpha_(glass)=9xx10^(-6)//^(@)C,gamma_(Hg)=180xx10^(-6)//^(@)C)`
View SolutionThe coefficient of linear expansion of crystal in one direction is `alpha_(1)` and that in every direction perpendicular to it is `alpha_(2)`. The coefficient of cubical expansion is
View SolutionThe real coefficient of volume expansion of glycerine is `0.000597per^(@)C` and linear coefficient of expansion of glass is `0.000009par^(@)C` . Then the apparent volume coefficient of glycerine is
View SolutionThe coefficient of apparent expansion of a liquid is `C` when heated in a copper vessel and is `S` when heated in a silver vessel. If `A` is the coefficient of linear expansion of copper, than that of silver is
View SolutionThere are two sphers of same radius and material at the same temperature but one being solid while the other hollow. Which sphere will expand more if they are given the same amount of heat ?
View SolutionIn the previous problem, same heat is given to two sphere, which will expand more
View SolutionA solid metal ball has a spherical cavity. If the ball is heatd, the volume of the cavity will
View SolutionThe temperature of water at the surface of a deep lake is `2^@C`. The temperature expected at the bottom is
View SolutionWhen water is heated from `0^(@)C` to `10^(@)C` , its volume
View SolutionA metal sheet with a cricular hole in heated. The hole
View SolutionTwo holes of unequal diameters `d_(1)` and `d_(2)(d_(1)gtd_(2))` are cut in metal sheet is heated
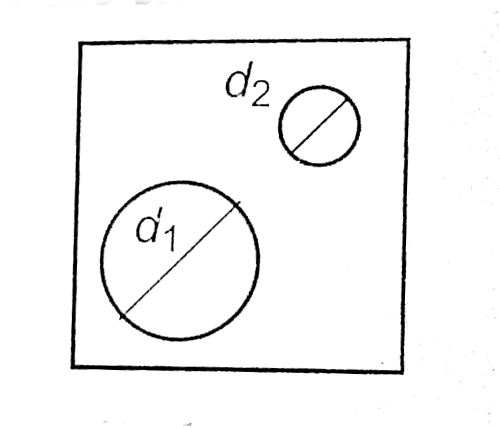
View SolutionIn the previous question, the distance between the hole will
View SolutionA metal rod is shaped into a ring with a small gap. If this is heated,
(i) the length of the rod will increase
(ii) the gap will decrease
(iii) the gap will increase
(iv) the diameter gof the ring will increase in the same ratio as the blength of the rod
View SolutionA the temperature is increased, the time period of a pendulum
View SolutionA second's pendulum gives correct time at `25^(@)C` . The pendulum shaft is thin and is made of steel. How many second will it lose per day at g`35^(@)C` ? `(alpha_(steel)=11xx10^(-5)//^(@)C)`
View SolutionA steel rod of length `25cm` has a cross-sectional area of `0.8cm^(2)` . The force required to stretch this rod by the same amount as the expansion produced by heating it through `10^(@)C` is `(alpha_(steel)=10^(-5)//^(@)C` and `Y_(steel)=2xx10^(10)N//m^(2))`
View SolutionTwo metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young module `Y_(1)` and `Y_(2)` , and coefficient of linear expansion `alpha_(1)` and `alpha_(2)` . The junction between the rod does not shift and the rods are cooled
View SolutionAn aluminum sphere is dipped into water as `10^@C`. If the temperature is increased, the force of buoyancy
View SolutionA solid with coefficient of linear expansion `aplha` just floats in a liquid whose coefficient of volume expansion is `gamma` . If the system is heated, the solid will
View SolutionA metal ball is being weighed in liquid whose temperature is raised continuously. Then the apparent weight of the ball
View SolutionA metal ball immersed in alcohol weights `W_1` at `0^@C` and `W_2` at `50^@C`. The coefficient of expansion of cubical the metal is less than that of the alcohol. Assuming that the density of the metal is large compared to that of alcohol, it can be shown that
View SolutionA block of wood is floating on water at `0^(@)C` with a certain volume `V` above water level. The temperature of water is slowly raised to `20^(@)C` . How does the volume `V` change with the rise of temperature ?
View SolutionWhen a block of iron in mercury at `0^@C,` fraction `K_1`of its volume is submerged, while at the temperature `60^@C,` a fraction `K_2` is seen to be submerged. If the coefficient of volume expansion of iron is `gamma_(Fe)` and that of mercury is `gamma_(Hg),` then the ratio `(K_1)//(K_2)` can be expressed as
View SolutionA solid whose volume does not change with temperature floats in a liquid. For two different temperatures `t_1` and `t_2` of the liqiud, fraction `f_1` and `f_2` of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to
View SolutionIn a vertical `U`-tube containing a luquid, the two arms are maintained at different temperatures, `t_(1)` and `t_(2)` . The liquid coplumns in the two arms have heights `l_(1)` and `l_(2)` respectively. The coefficient o0f volume expansion of the liquid is equal to

View Solution
EXERCISES questions and complete solutions for chapter TEMPERATURE AND THERMAL EXPANSION of CP SINGH PHYSICS (HINGLISH) of Class 11