Complete Solutions to Exercises of chapter HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HEAT TRANSFER |
| CP SINGH | Exercises |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
When two ends of a rod wrapped with cotton are maintained at differences and after some time every point of the rod attains a constant temperature, then
View SolutionThe thermal conductivity of a rod depends on
01:54View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
01:51View SolutionIn a room containing air, heat can go from one place to another
02:23View SolutionThe two ends of uniform rod of thermal conductivity `K` are maintained at different but constant temperatre. The temperature gradient at any point on the rod is `d theta // dx`. The heat flow per unit time per unit cross-section of the rod is `I`.
(i) `(d theta)/(dx)` is the same for all point on the rod
(ii) `I = K (d theta)/(dx)`View SolutionWhich of the following circular rods (given radius `r` and length `l`) each made of the same material and whose ends are maintained at the same temperature will conduct most heat?
02:56View SolutionTwo rods `A` and `B` are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are `A_(1)` and `A_(2)` and thermal conductivities `K_(1)` and `K_(2)`. The rate of heat transmission in the two rods will be equal, if
01:57View SolutionThe temperature gradient in a rod of `0.5 m` length is `80^(@)C//m`. It the temperature of hotter end of the rod is `30^(@)C`, then the temperature of the cooler end is
01:02View SolutionA cylindrical rod having temperature `T_(1)` and `T_(2)` at its ends. The rate of flow of heat is `Q_(1) cal//sec`. If all the linear dimensions are doubled keeping temperature constant, then rate of flow of heat `Q_(2)` will be
02:56View SolutionThe heat is flowing through two cylinderical rods of same material. The diameters of the rods are in the ratio `1:2` and their lengths are in the ratio `2:1`. If the temperature difference between their ends is the same, the ratio of rates of flow of heat through them will be
02:05View SolutionTwo identical vessels are filled with equal amounts of ice. The vessels are made from different materials. If the ice melts in the two vessels in times `t_(1) and t_(2)` respectively, then their thermal conductivities are in the ratio
02:53View SolutionOne end of a themally insulated copper rod of length `1 m` long and of `10 cm^(2)` in X-section is immersed in boiling water `(100^(@)C)` and the other in ice `(0^(@)C)` . If `K_(Cu) = 0.92 cal//cm.//s//.^(@)C` and `L_(ice) = 80 cal//g`, the ice that will melt per minute is
02:59View SolutionA glass window conducts out a certain quantity of heat per second when the inside temperature is `10^(@)C` and the outside temperature is `- 10^(@)C`. The same quantity of heat will be conductued in through the window per second when the inside temperature is `- 43^(@)C` and the outside temperature is
View SolutionTwo walls of thicknes `l_(1)` and `l_(2)` and ther-mal condctivities `K_(1)` and `K_(2)` are in contact In the steady state, if the temperature at the outer faces are `T_(1)` and `T_(2)` find the temperature at the common wall .
02:47View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities `K_(1)` and `K_(2)`. The equivalent thermal conductivity of the slab is
03:28View SolutionTwo rods of the same length and diameter, having thermal conductivities `K_(1)` and `K_(2)`, are joined in parallel. The equivalent thermal conductivity to the combinationk is
02:18View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities `K` and `2K` respectively. The equivalent thermal conductivity of the slab is
02:41View SolutionA cylinder of radius R made of a material of thermal conductivity `K_1` is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity `K_2`. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
03:41View SolutionA long metallic bar is carrying heat from one of its ends to the other end under steady-state. The variation of temperature `theta` along the length x of the bar from its hot end is best described by which of the following figures?
03:52View Solution`A` and `B` are two points on uniform metal ring whose centre is `O` The angle `AOB =theta` A and `B` are maintaind at two different constant temperatures When `theta =180^(@)` the rate of total heat flow from `A` to `B` is `1.2W` When `theta =90^(@)` this rate will be .
04:53View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 03:07View Solution
03:07View SolutionThree rods `A, B` and `C` of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of `A` and `B`, in equilibriu, is
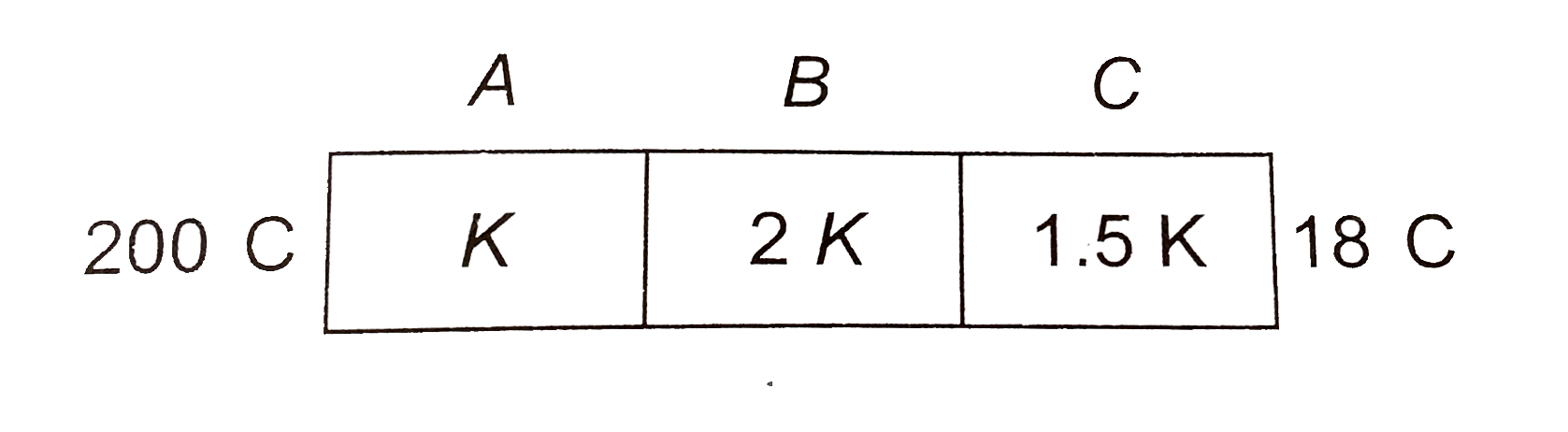 05:36View Solution
05:36View SolutionThree rods of same dimensions have thermal condutivity `3K,2K` and `K` They are arranged as shown in Then the temperature of the junction in steady state is
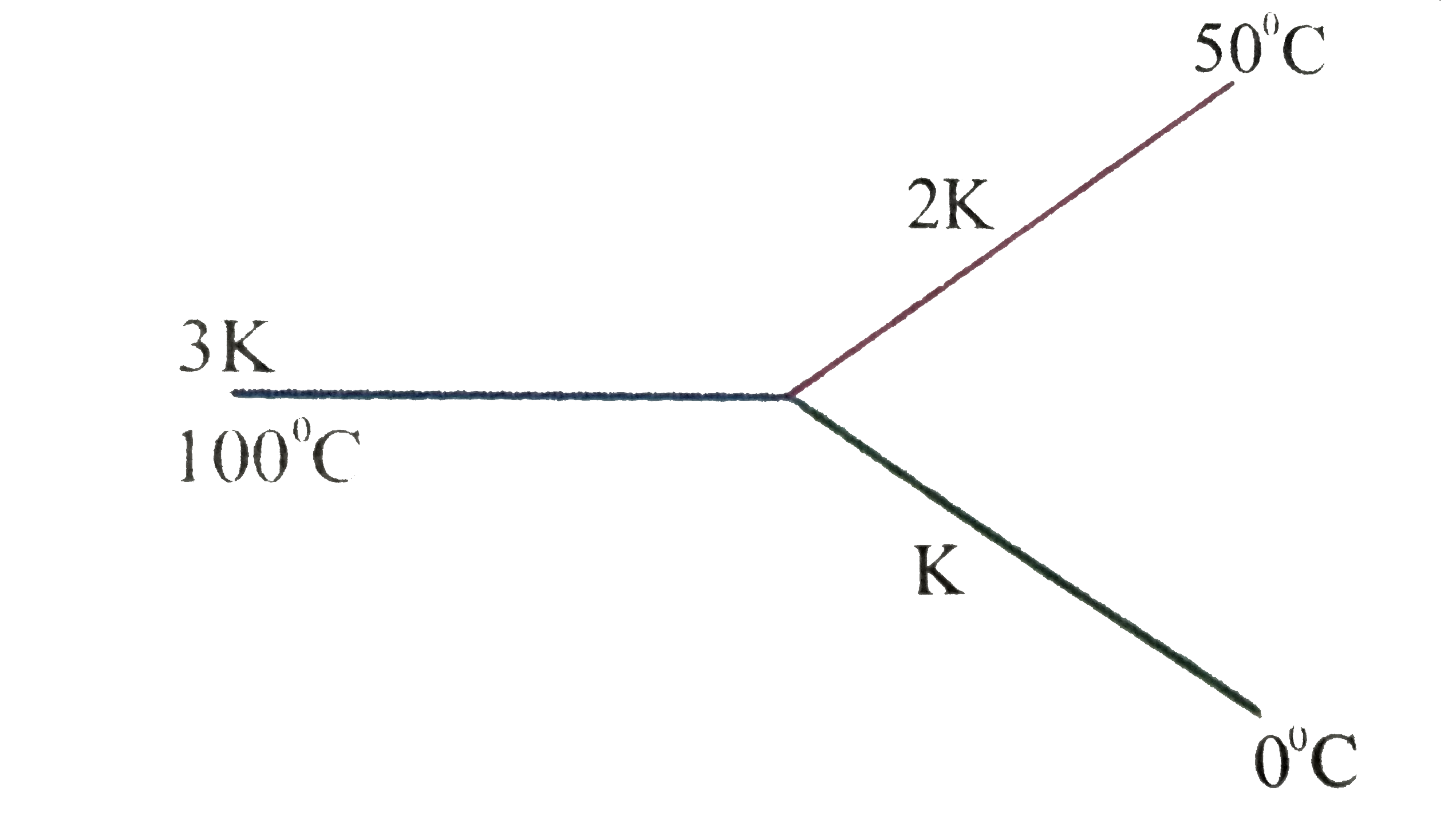 .03:01View Solution
.03:01View SolutionA rod `CD` of thermal resistance `5.0KW_(-1)` is joined at the middle of an identical rod `AB` as shown in figure. The ends `A`,` B` and `D` are maintained at `100^(@)C` , `0^(@)C` and `25^(@)C` respectively. Find the heat current in `CD`.
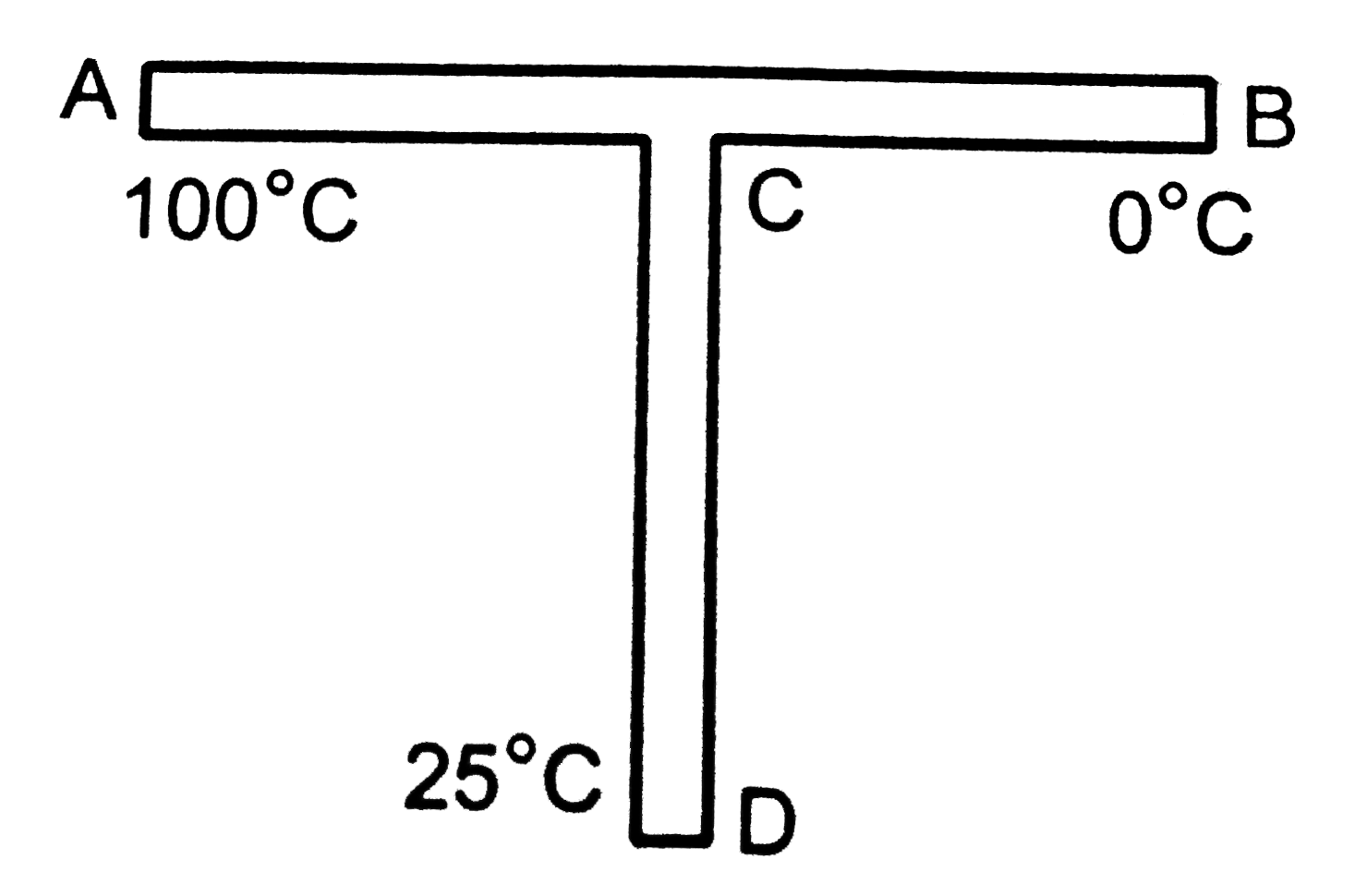 05:56View Solution
05:56View SolutionConsider the situation shown in figure. The frame is made of the same material and has a uniform cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at `100^(@)C` is `130J` .
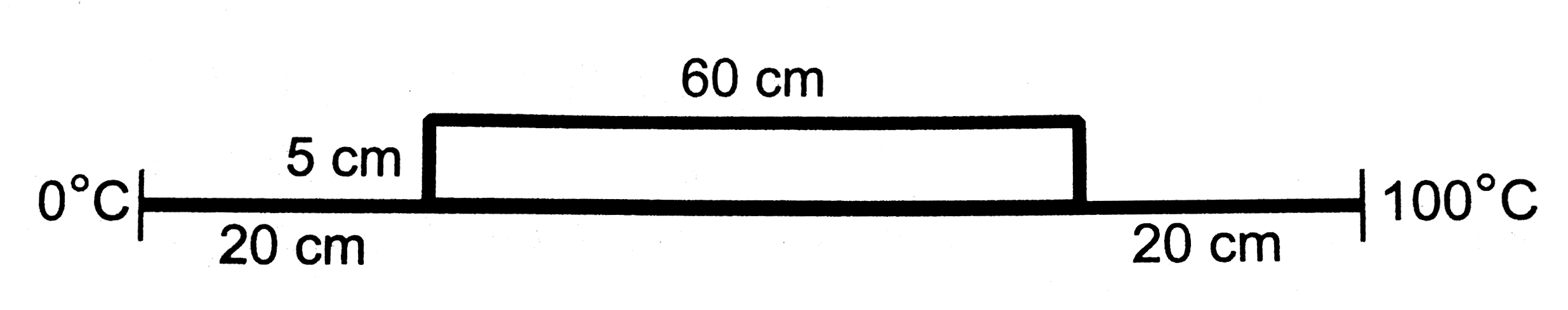 06:03View Solution
06:03View SolutionA wall has two layers A and B each made of different materials. Both the layers have the same thickness. The thermal conductivity of materials A is twice of B. Under thermal equilibrium temperature difference across the layer B is `36^@C`. The temperature difference across layer A is
05:16View Solution
Three rods of same dimensions are arranged as shown in Fig. They have thermal conductivities `K_1`,`K_2` and `K_3`. The points P and Q are maintained at different temperature for the heat to flow at the same rate along PRQ and PQ. Which of the following options correct?04:28View SolutionThree rods of identical cross-sectional area and made from the same metal from the sides of an isosceles triangle ABC, right-angled at B. The point A and B are maintained at temperatures T and `sqrt(2)` T respectively. In the steady state, the temperature of the point C is `T_c.` Assuming that only heat conduction takes places, `T_c//T` is
04:59View SolutionFive rods of same dimensions are arrranged as shown in the figure. They have thermal conductivities `K_(1), K_(2), K_(3), K_(4)` and `K_(5)`. When points `A` and `B` are maintained at different themperature, no heat flows through the central rod if
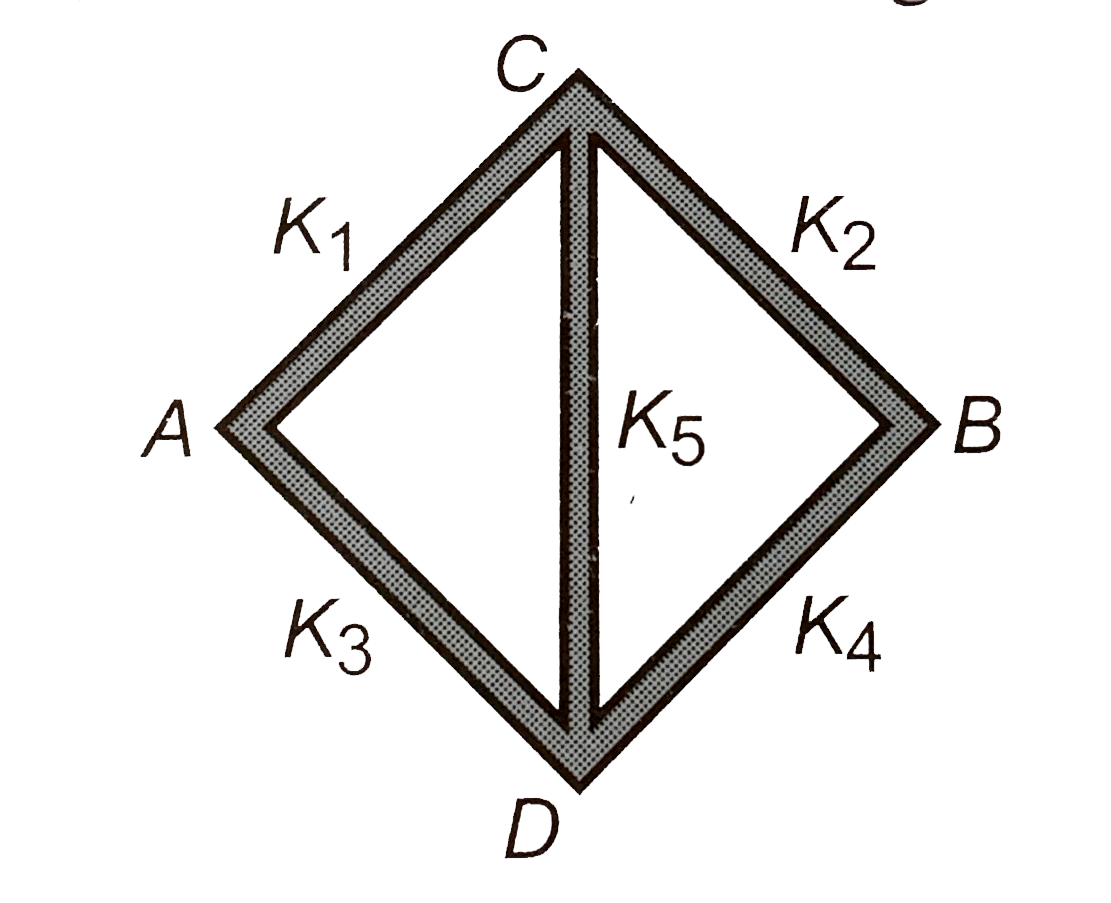 03:06View Solution
03:06View SolutionConsider the 6 idential rods as shown in figure, the conductivity of `x` is double that of `y`. The temperatre of the junciton `B` is
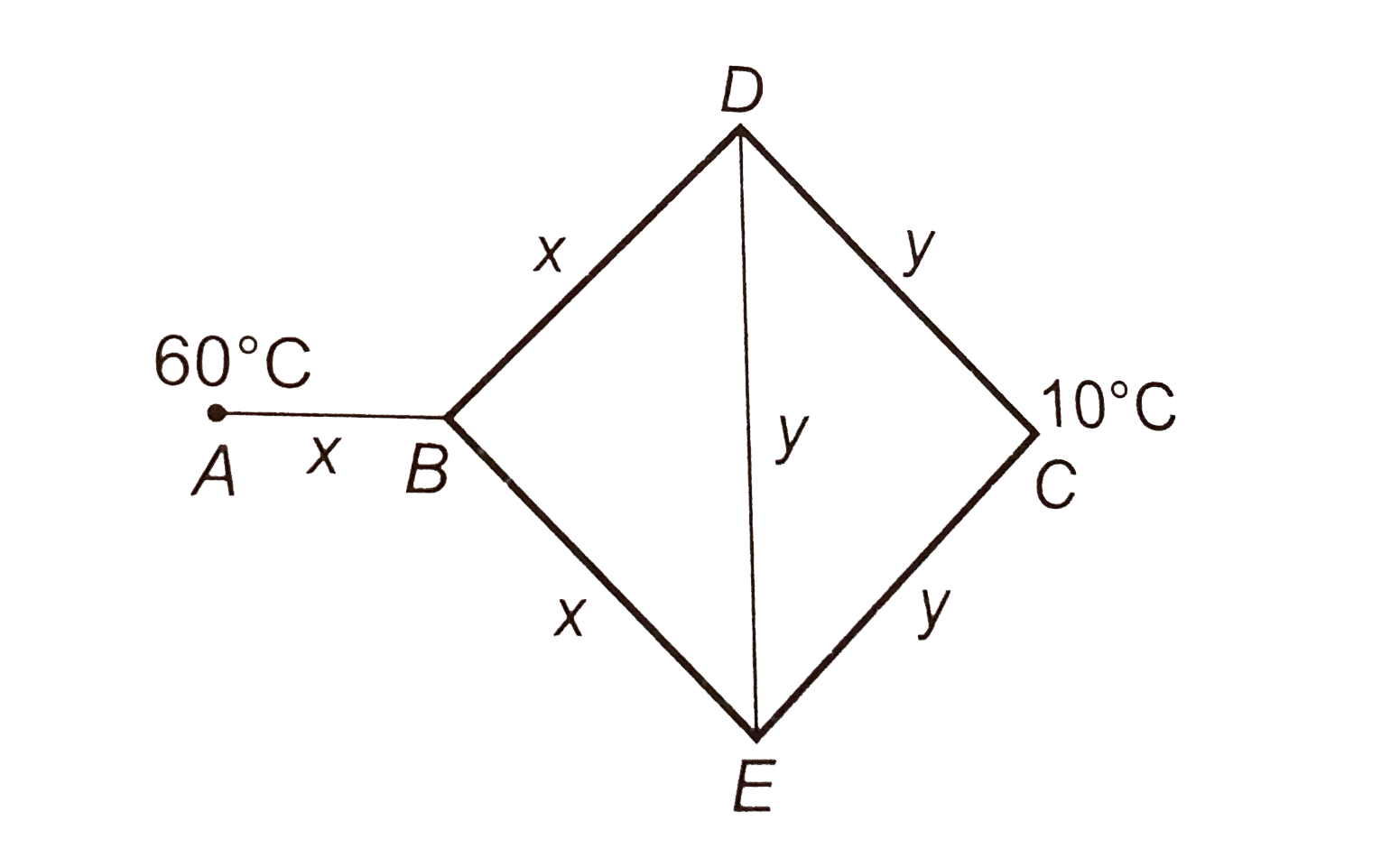 View Solution
View SolutionA cylindrical rod with one end in a steam chamber and the other end in ice results in melting of 0.1 g of ice per second. If the rod is replaced by another with half the length and double the radius of the first and if the thermal conductivity of material of second rod is 1/4 that of first, the rate at which ice melts in `g//s` will be
05:52View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at `100^@C` and the other containing ice at `0^@C`. In the second case, the rods are joined end to end and connected to the same vessels. Let `q_1 and q_2` gram per second be the rate of melting of ice in the two cases respectively. The ratio `q_1/q_2` is
(a) `1/2` (b)`2/1` (c)`4/1` (d)`1/4`04:37View SolutionA metal rod AB of length 10x has its one end A in ice at `0^@C`, and the other end B in water at `100^@C`. If a point P one the rod is maintained at `400^@C`, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is `540cal//g` and latent heat of melting of ice is `80cal//g`. If the point P is at a distance of `lambdax` from the ice end A, find the value `lambda`. [Neglect any heat loss to the surrounding.]
04:16View SolutionA composite block is made of slabs A,B,C,D and E of different thermal conductivities (given in terms of a constant K and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks. Then in steady state
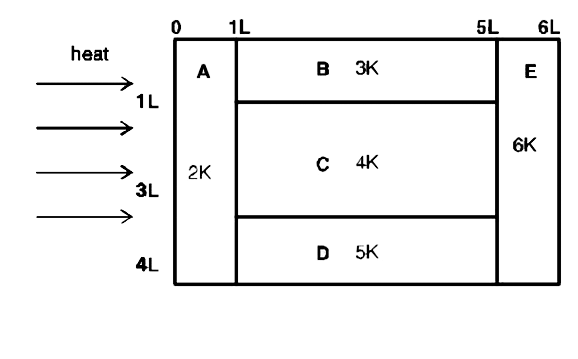 07:42View Solution
07:42View SolutionAccording to the experiment of Ingen Hauze the relation between the thermal conductivity of a metal rod is `K` and the length of the rod whenever the wax melt is
View SolutionIf the ratio of coefficient of thermal conductivity of silver and copper is `10 : 9`, then the ratio of the length upto which wax will melt in Ingen Hauze experiment will be
01:34View SolutionTemperature of water at the surface of lake is `- 20^(@)C`. Then temperature of water just below the lower surface of ice layer is
02:12View SolutionIce starts forming in lake with water at `0^(@)C` and when the atmospheric temperature is `-10^(@)C`. If the time taken for `1 cm` of ice be `7` hours. Find the time taken for the thickness of ice to change from `1 cm` to `2 cm`
09:24View SolutionA `5 cm` thick ice block is there on the surface of water in a lake. The tmeperature of air `- 10^(@)C`, how muct time it will take to double the thickness of the block?
`(L = 80 cal//g, K_(ice) = 0.004 cal//s-K, d_(ice) = 0.92 g cm^(-3))`02:51View SolutionIn a 10 m deep lake, the bottom is at a constant temperature of `4^(@)C`. The air temperature is constant at `- 4^(@)C. K_(ice) = 3 K_(omega)`. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
03:37View SolutionIn heat transfer, which method is based on gravitation ?
View SolutionWhen fluids are heated from the bottom, convection currents are prodcued because
View SolutionIf a liquid is heated in weightlessness, the heat is tramsmitted thruogh
View SolutionIn summer, a mild wind is often found on the shore of a clam river. This is caused due to
02:22View SolutionThe process in which rate of transfer of heat maximum is .
01:47View SolutionWhich of the following law states that "good absorbers of heat are good emitters"
01:20View SolutionFor a perfectly black body, its abosrpitve power is
01:32View SolutionAt a certain temperature for given wavelength, the ratio of emissive power of a body to emmisve power of black body in same circumstance in known as
01:50View SolutionThree objects coloured black, gray and white can withstand hostile conditions upto `2800^(@)C`. These objects are thrown into a furance where each of them attains a temperature of `2000^(@)C`. Which object will glow brightest?
01:52View SolutionAn ideal Black-body at room temperature is thrown into a furnace. It is observed that
01:41View SolutionA hot body will radiate maximum energy if its surface is
01:25View SolutionA black body does not
(i) emit radiation (ii) absorb radiation
(iii) reflect radiation (iv) refract radiation01:25View SolutionThe thermal radiation emited by a body is proportional to `T^(n)` where `T` is its absolute temperature. The value of `n` is exactly 4 for
01:26View SolutionA spherical black body with a radius of 12 cm radiates 450 watt power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be
01:47View SolutionA black body at `227^(@)C` radiates heat at the rate of `7 cal cm^(-2) s^(-1)`. At a temperature of `727^(@)C`, the rate of heat radiated in the same unit will be
02:00View SolutionTwo spherical black bodies of radii `R_(1)` and `R_(2)` and with surface temperature `T_(1)` and `T_(2)` respectively radiate the same power. `R_(1)//R_(2)` must be equal to
02:08View SolutionTwo bodies `A` and `B` having equal surface areas are maintained at temperatures `10^(@)C` and `20^(@)C` . The thermal radiation emitted in a given time by `A` and `B` are in the ratio
01:33View SolutionTwo spheres of radii in the ratio `1 : 2` and densities in the ratio `2 : 1` and of same specific heat, are heated to same temperature and left in the same surronding. There are of cooling will be in the ratio
04:21View SolutionA piece of charcoal and a piece of shining steel of the same surface area are kept for a long time in an open lawn in bright sun.
02:10View SolutionIn a dark room with ambient temperature `T_(0)`, a black body is kept at a temperature `T`. Keeping the temperatre of the black body constant (at `T`) sunrays are allowed to fall on the black body through a hole in the roof of the dark room. Assuimng that here is no charge in the ambient temperature of room, which of following statement `is//are` correct (i) The quantity of radiation absorbed by the black body in unit time will increase
(ii) Since emissivity = absorptivity, hence, the equantity increase
(iii) Black body radiation emitted by black body in unit time in the visible spectrum
(iv) The reflected energy in unit time by the black body remains sameView SolutionThree very large plates of same area are kept parrallel and close to each other. They are considered as ideal black surfaces and have high thermal conductivity. The first and third plates are maintained at temperatures 2T and 3T respectively. The temperature of the middle (i.e., second) plate under steady state condition is
03:03View SolutionA solid at temperature `T_(1)` is kept in an evacuated chamber at temperature `T_(2)gtT_(1)` . The rate of increase of temperature of the body is proportional to
02:18View SolutionA system `S` receives heat continuously from an electric heater of power `10 W`. The temperature of `S` becomes constant at `50^(@)C` when the surrounding temperature is `20^(@)C`. After the heater is switched off, `S` cools from `35.1^(@)C` to `34.9^(@)C` in `1 minute`. the heat capacity of `S` is
06:40View SolutionA spherical black body of radius `r` radiates power `P`, and its rate of cooling is `R`
(i)`P prop r`
(ii)`P prop r^(2)`
(iii)`R prop r^(2)`
(iv)`R prop (1)/(r)`02:58View SolutionThe temperature of an isolated black body falls from `T_(1)` to `T_(2)` in time `t`. Let `c` be a constant
View SolutionA solid cube and a solid sphere of the same material have equal surface area. Both are at the same temperature `120^(@)C`, then
03:25View SolutionA solide sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature
(i) Both will emit equal amount of radiation per unit time in the beginning
(ii) Both will absorb equal amount of radiation from the surrounding in the beginning
(iii) The initial rate of cooling `dT//dt` will be same for the two spheres
(iv) The two spheres will have equal temperatures at any instant03:06View SolutionA sphere at temperature `600 K` is placed in an enviroment to temperature is `200 K`. Its cooling rate is `H`. If its temperature reduced to `400 K` then cooling rate in same enviorment will become
03:00View SolutionTwo metallic spheres `S_1 and S_2` are made of the same material and have got identical surface finish. The mass of `S_1` is thrice that of `S_2`. Both the spheres are heated to the same high temperature and placed in the same room having lower temperature but are thermally insulated from each other. the ratio of the initial rate of cooling of `S_1` to that of `S_2` is
`(a)1/3 (b)1/(sqrt3) (c) (sqrt3)/1 (d) (1/3)^(1/3)`03:22View SolutionA sphere, a cube and a thin circular plate, all having the same mass and made of the same material are heated to the same temperature and them allowed to cool. Which of them cools fastest ?
01:42View SolutionIf the temperature of the sun were to increase form T to 2T and its radius from R to 2R, then the ratio of the radiant energy received on earth to what it was previously will be
02:07View SolutionIf the radius of a star is `R` and it acts as a black body, what would b the temperature of the star, in which the rate of energy production is `Q`?
01:07View SolutionThe radiant energy from the Sun incident normally at the surface of earth is `20kcal//m^(2)` min What would have been the radiant energy incident normally on the earth if the sun had a temperature twice of the present one ? .
02:36View SolutionAssuming the sun to have a spherical outer surface of radius `r` radiating like a black body at temperature `t^(@)C`. The power received by a unit surface (normal to the incident rays) at a distance `R` from the centre of the sun is
where `sigma` is the Stefan's constant.03:36View SolutionAssuming the Sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant powered incident of Earth at a distance r from the sun
where `r_0` is the radius of the Earth and `sigma` is Stefan's constant.05:44View SolutionThe sun radiates energy in all directions. The average radiations received on the earth surface from the sun is `1.4 "kilowatt"//m^2`. The average earth-sun distance is `1.5 xx 10^11` meters. The mass lost by the sun per day is.
05:12View SolutionNewton's law of cooling is a special case of .
03:27View SolutionA body cools from `50^(@)C` to `40^(@)C` in 5 min. The surroundings temperature is `20^(@)C`. In what further times (in minutes) will it cool to `30^(@)C` ?
02:17View SolutionIn the previous question will be its temperature 5 min after reaching `40^(@)C`?
02:37View SolutionA body with an initial temperature `theta_(1)` is allowed to cool in a surrounding which is at a constant temperature of `theta_(0) (theta lt theta_(1))` Assume that Newton's law of cooling is obeyed Let `k =` constant The temperature of the body after time t is best experssed by .
02:48View SolutionA hot liquid is kept in a big room. Its temperature is plotted as a function of time. Which of the following curves may present the plot ?
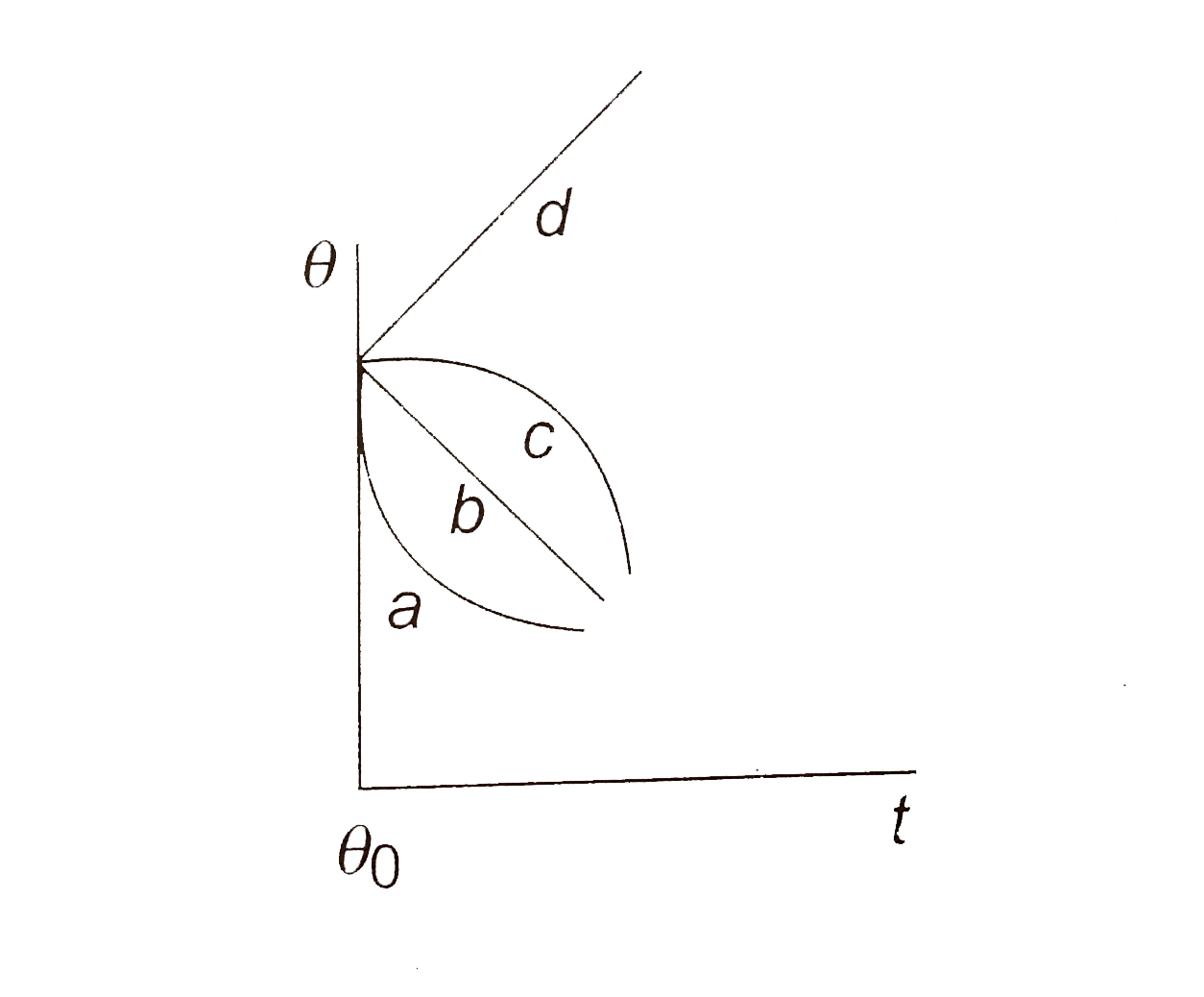 View Solution
View SolutionA liquid in a beaker has temperature `theta(t)` at time t and `theta_0` is temperature of surroundings, then according to Newton's law of cooling the correct graph between `log_e( theta-theta_0)` and t is :
02:00View SolutionA hot liquid is kept in a big room. The logarithm of the numerical value of the temperature difference between the liquid and the room is plotted against time.The plot will be very nearly
03:46View SolutionTwo solid spheres of radii `R_(1)` and `R_(2)` are made of the same material and have similar surfaces. These are raised to the same temperature and then allowed to cool under identical conditions. The ratio of their initial rates of loss of heat are
01:59View SolutionIn previous problem, the ratio of the initial rates of cooling (i.e., rates of fall of temperature) is
02:28View SolutionRelation between the colour and the temperature of a star in given by
View SolutionA black body has maximum wavelength `lambda_(m)` at temperature `2000 K`. Its corresponding wavelength at temperature 3000 will be
01:10View SolutionThe intensity of radiation emitted by the sun has its maximum value at a wavelength of 510 nm and that emitted by the North star has the maximum value at 350 nm. If these stars behave like black bodies, then the ratio of the surface temperatures of the sun and the north star is
01:45View SolutionThe plots of intensity versus wavelength for three black bodies at temperatures `T_(1),T_(2)` and `T_(3)` respectively are shown in Their temperatures are shown in How their temperatures are related ?
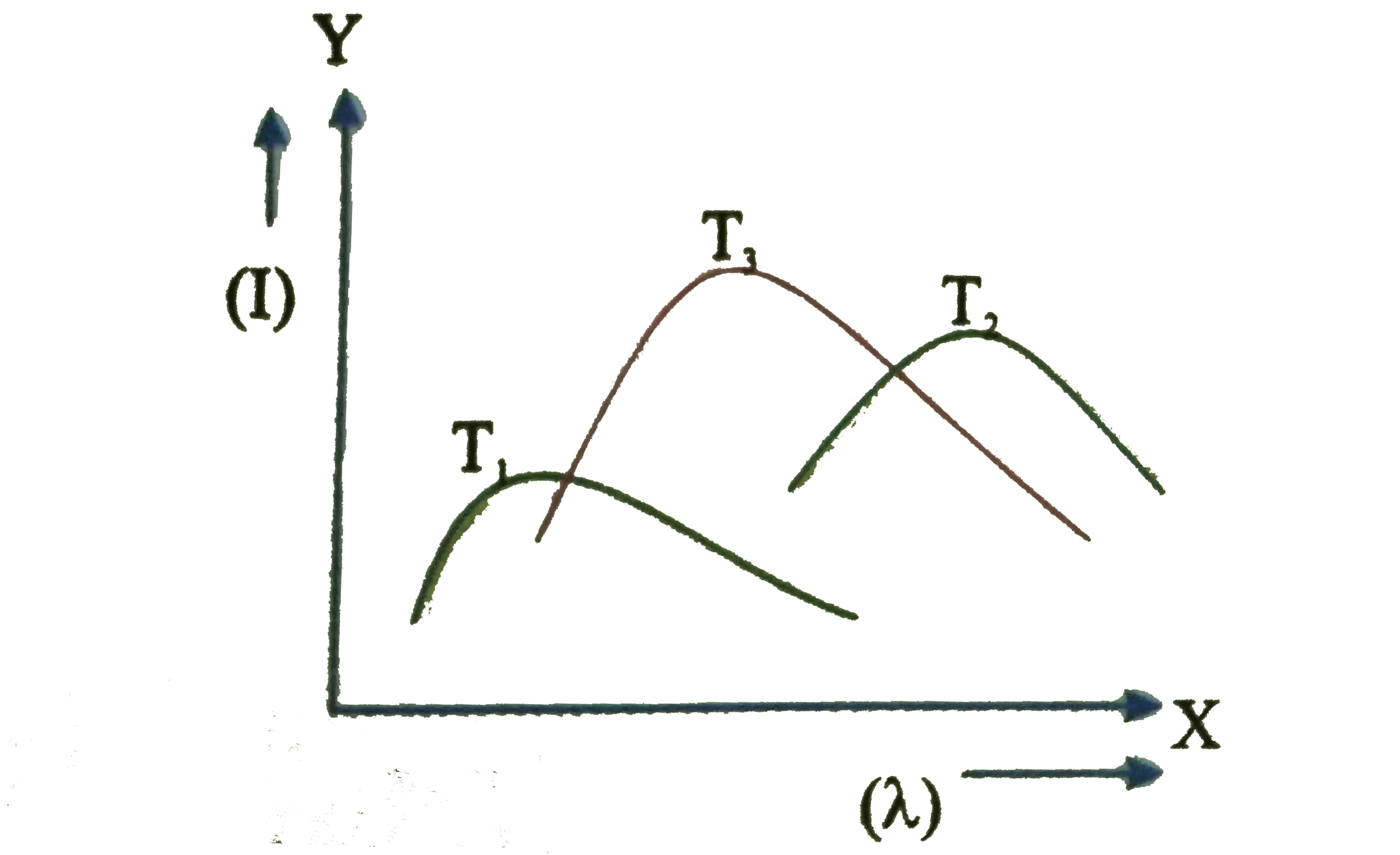 .02:19View Solution
.02:19View SolutionA black body is at a temperature of `2800K` The energy of radiation emitted by this object with wavelength between `499nm` and 500 nm is `U_(1)` between 999nm and 1000nm is `U_(2)` and between 1499 nm and 1500 nm is `U_(3)` The Wien's constant `b =2.80 xx 10^(6)` nm `K` Then .
03:08View SolutionThe power radiated by a black body is `P` and it radiates maximum energy around the wavelength `lambda_(0)` If the temperature of the black body is now changed so that it radiates maximum energy around a wavelength `3lambda_(0)//4` the power radiated by it will increase by a factor of .
02:23View SolutionA heater body emits radiation which has maximum intensity near the frequency `v_(0)` The emissivity of the material is `0.5` . If the absolute temperature of the body is doubled,
03:09View SolutionThree discs, A, B and C having radii 2m, 4m and6m respectively are coated with carbon black on their outer surfaces. The wavelengths corresponding to maximum intensity are `300nm, 400nm` and `500 nm`, respectively. The power radiated by them are `Q_A, Q_B and Q_C` respectively
(a) `Q_A` is maximum (b) `Q_B` is maximum (c) `Q_C` is maximum (d) `Q_A = Q_B = Q_C`03:02View SolutionMake the pairs
`{:(A.,"Thermal conductivity",(i),ML T^(-3)K^(-1)),(B.,"Thermal resistance",(ii),M^(-1)L^(-2)T^(3)K),(C.,"Stefan's constant",(iii),M T^(-3)K^(-4)),(D.,"Wien's constant",(iv),L K):}`View Solution
Exercises questions and complete solutions for chapter HEAT TRANSFER of CP SINGH PHYSICS (HINGLISH) of Class 11
