Complete Solutions to Example of chapter HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HEAT TRANSFER |
| CP SINGH | Example |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A metal frame of total length `50 cm` ad croos-sectional area `0.20 cm^(2)` froms five sides of a regular hexagon. The free ends are maintained at `20^(@)C` and `40^(@)C`. Find the rate of heat flow through a cross-section of the frame `(K = 50 W//m^(@)C)`
View Solution(a) One end of a steel rod `(K = 46 J//m-s-.^(@)C)` length `1.0 m` is kept in ice at `0^(C )` and the end is kept in boling water at `100^(@)C`. The area of cross-section of the rod is `0.4 cm^(2)`. Assuming no heat loss to atmosphere, find the mass of of the ice melting per second. Latent heat of fusion of ice `= 3.36 xx 10^(5) J//kg`
(b) An icebox almost completely filled with ice at `0^(@)C` is dipped into a large volume of water at `20^(@)C`. The box has walls of surface area `2400 cm^(2)`, thickness `2.0 mm` and thermal conductivity `0.6 W//m-^(@)C`. Calculate the rate at which the ice melts in the box. Latent heat of fusion if ice `= 3.4 xx 10^(5) J//kg`.
View SolutionWater is boiled in a container having a bottom of surface area `25cm^(2)` , thickness `1.0mm` and thermal conductivity `50Wm^(-1).^(@)C^(-1)` , `100g` of water is converted into steam per minute in the steady state after the boiling starts.Assuming that no heat is lost to the atmosphere, calculate the temperature of the lower surface of the bottom. Latent heat of vaporization of water `=2.26xx10^(6)Jkg^(-1)` .
View SolutionA composite slab is prepared by pasting two plates of thickness `L_(1)` and `L_(2)` and thermal conductivites `K_(1)` and `K_(2)` . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionFind equivalent thermal conductivity in the following cases:
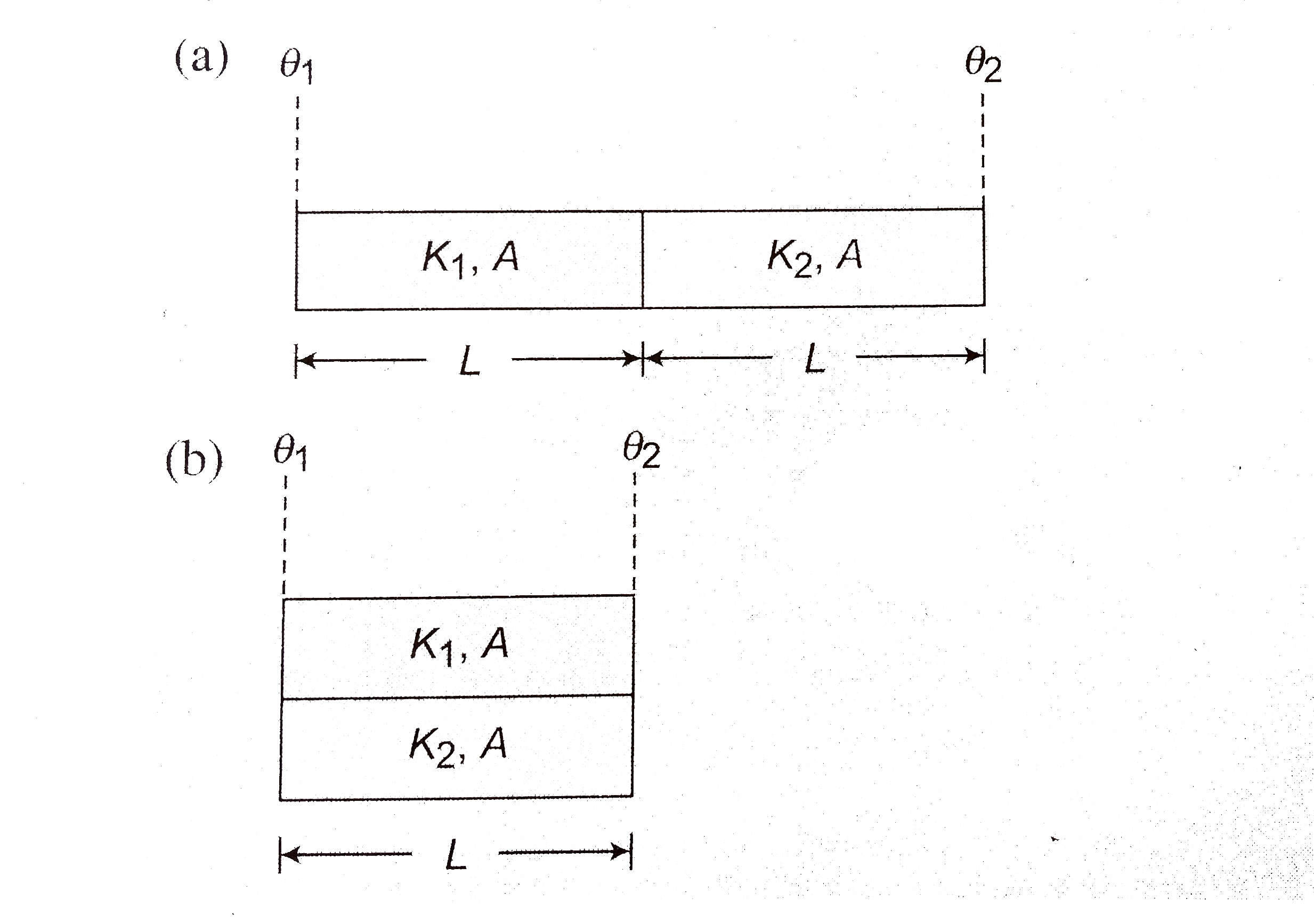

View SolutionThe two rods shown in figure have identical geometrical dimension. They are in contact with two heat baths at temperature `100^(@)C` and `0^(@)C` . The temperature of the junction is `70^(@)C` . Find the temperature of the junction if the rods are interchanged.

View SolutionAn aluminium rod and copper rod of equal length `1 m` and cross-sectional area `1 cm^(2)` are welded as shown. `K_(A1) = 200 W//m^(@)C, K_(Cu) = 400 W//m^(@)C`. Find heat current


View SolutionThe ends of a metre stick are maintained at `100^(@)C` and `0^(@)C` . One end of a rod is maintained at `25^(@)C` . Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
View SolutionFigure shows an aluminium rod joined to a copper rod. Each of the rods has a length of `20cm` and area of cross section `0.20cm^(2)` . The junction is maintained at a constant temperature `40^(@)C` and the two ends are maintained at `80^(@)C` . Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivities are `K_(Al)=200Wm^(-1).^(@)C^(-1)` . and `K_(Cu)=400Wm^(-1).^(@)C^(-1)` .

View Solution(a) Three rod of lengths `20 cm` each and area of cross-section `1 cm^(2)` are joined to form a triangle `ABC`. The conductivities of the rods are `K_(AB) = 50 J//m-s-.^(@)C, K_(BC) = 200 J//m-s-.^(@)C` and `K_(AC) = 400 J//m-s-.^(@)C`. The junctions `A, B` and `C` are maintained at `40^(@)C`, `80^(@)C` and `80^(@)C` respectively. Find the rate of heat flowing through the rods `AB, AC` and `BC`.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View SolutionThe three rods shown in figure have identical geometrical dimensions. Heat flows from the hot end at a rate of `40W` in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c). Thermal conductivities of aluminium and copper are `200Wm^(-1).^(@)C^(-1)` and `00Wm^(-1).^(@)C^(-1)` respectively.
View SolutionA room has a window fitted with a single `0.1mxx2.0m` glass of thickness 2mm. (a) Calculate the rate of heat flow through the closed window when the temperature inside the room is `32^(@)C` and that outside is `40^(@)C` . (b) The glass is now replaced by two glasspane, each having a thickness of `1mm` and separated by a distance of `1mm`. Calculate the rate of heat flow under the same condition of temperature. Thermal conductivity of window glass `=1.0Js^(-1)m^(-1).^(@)C^(-1)` and that of air `=0.025Js^(-1)m^(-1).^(@)C^(-1)` .
View SolutionThree identical rods are joined in series as shown. Their thermal conductivities are `K, K//2` and `K//3` respectively. At steady, if the free ends of rods are at `100^(@)C` and `20^(@)C` respectively. Determine the temperature at two junction points. Also find the equivalent thermal conductivity.
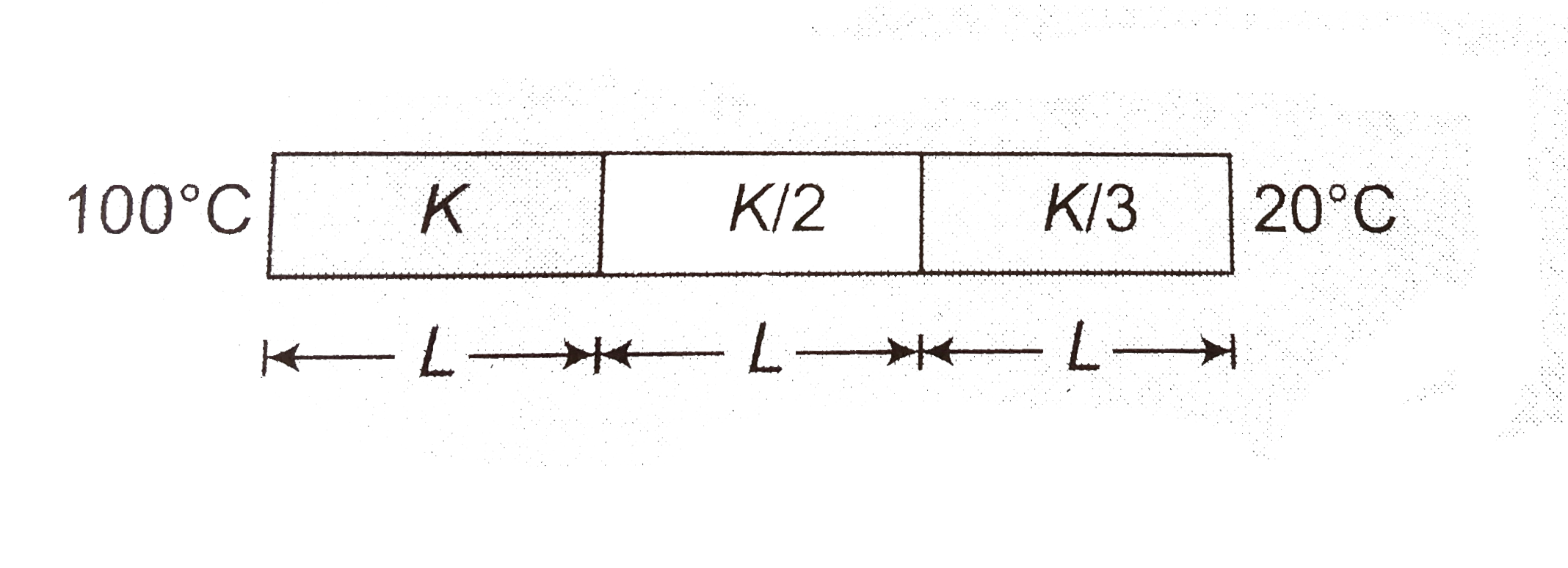
View SolutionIn the following situations, the length and area of cross-section of each rod is same. Find temperature `theta` at junction of rods.
(a)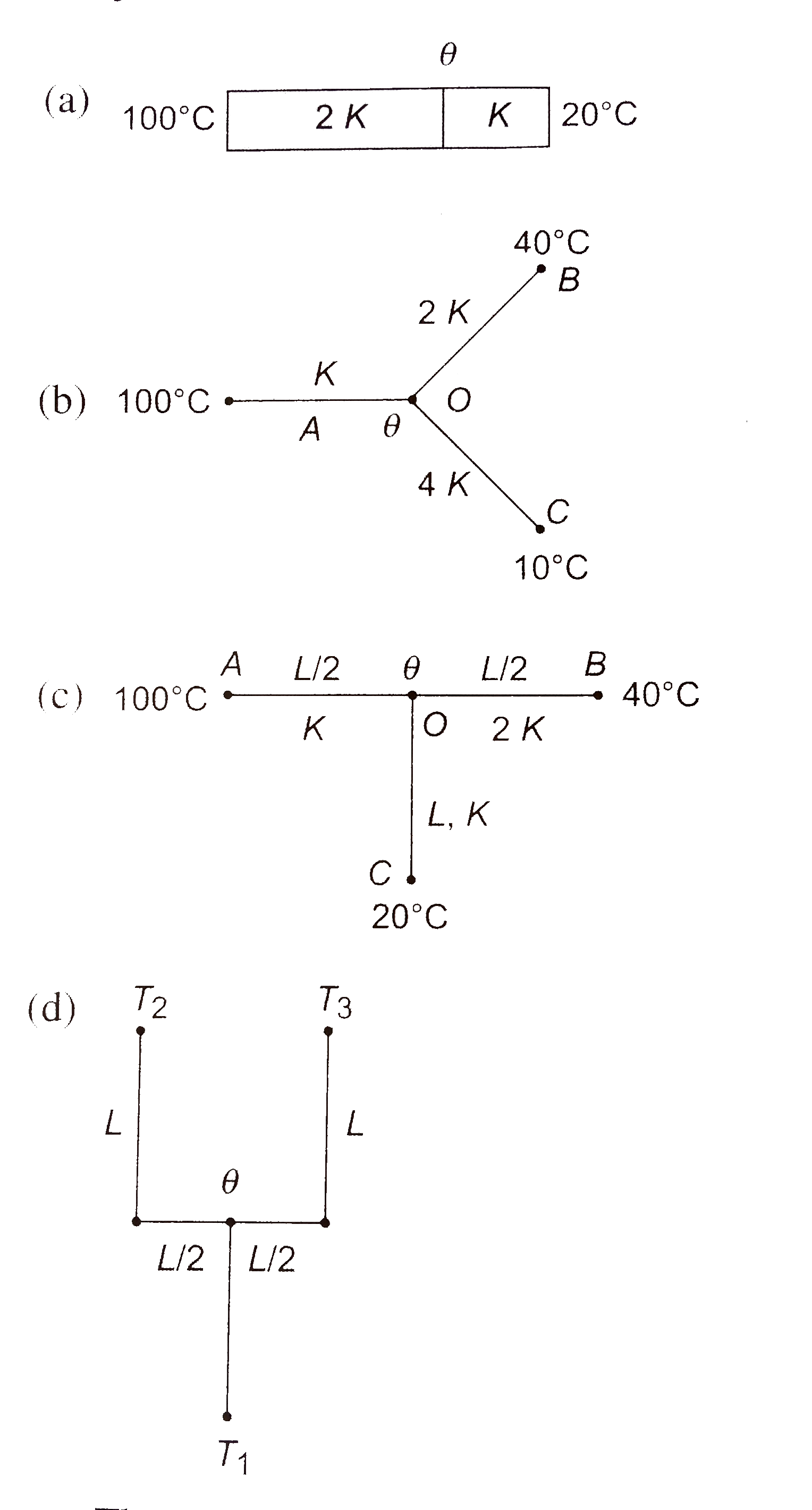
(b)
(c )
(d)
The thermal conductivity of each rod is `K`.
View SolutionA rod of negligible heat capacity has length `L`, area of cross-section `A` and thermal conductivity `K`. The temperature of one end is maintained at `0^(@)C` and the other end is slowly linearly varied from `0^(@)C` to `theta_(0)^(@)C` in time `t_(0)` Assuming no loss of heat through the sides, find the total heat transimitted through the rod in time `t_(0)`
View SolutionOn a winter day when the atmospheric temperature drops to `-10^(@)C`, ice form on the surface of a lake.
(a) Calculate the rate of increases of thickness of the ice when `10 cm` of ice is already formed.
(b) Calculate the total time taken in forming `10 cm` of ice. Assume that the temperature of the entire water reaches `0^(@)C` before the ice starts froming. Density of water `= 1000 kg//m^(3)`, latent heat of fusion of ice `= 3.36 xx 10^(5) J//kg` and thermal conductivity of ice `= 1.7 W//m-^(@)C`. Neglect the expansion of water on freezing
View SolutionConsider the situation of the previous problem. Assume that the temperature of the water at the botton of the lake remains constant at `4^(@)C` as the ice forms on the surface (the heat required to maintain the temperature of the bottom layer may come from the bed of the lake). The depth of the lake is `1.0m`. Show that the thickness of the ice formed attains a steady state maximum value. Find this value. The thermal conductivity of water `=0.50Wm ^(-1).^(@)C^(-1)` . Take other relevent data form the previous problelm.
View SolutionCalculate the amount of heat radiated per second by a body of surface are `10 cm^(2)` kept in thermal equilibrium in a roomat temperature `27^(@)C`. The emissivity of the surface ` = 0.80` and Stefan's constant
`sigma ~= 6 xx 10^(-8) W//m^(2) K^(4)`
View SolutionA spherical tungsten piece of radius `(1)/(sqrt(pi)) cm` is suspended in an evacuated chamber maintained at `200 K`. The piece is maintained at `400 K` by heating it electrically. Find the rate at which the electrial energy must be supplied. The emissivity of tungsten is `0.50`, the Steafan constant `sigma` is `6.0 xx 10^(-8) W//m^(2)-K^(4)`
View SolutionA cubical block of mass `1.0kg` and edge `5.0cm` is heated to `227^(@)C` . It is kept in an evacuated chamber maintained at `27^(@)C` . Assming that the block emits radiation like a blackbody, find the rate at which the temperature of the block will decreases. Specific heat capacity of the material of the block is `400Jkg^(-1)K^(-1)` .
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperature. Assume that the emissivity of both the spheres is the same. Find the ratio of
(a) the rate of heat from the aluminium sphere to the rate of heat loss from the copper sphere and
(b) the rate of fall of temperature of the the aluminium sphere to the rate of fall temperature of teh copper sphere. The specific heat capacity of aluminium `= 900 J//kg -^(@)C` and that of copper `= 390 J//kg-^(@)C`. The density of copper is `3.4 times the density of aluminium.
View SolutionOne end of a rod length `20cm` is inserted in a furnace at `800K`. The sides of the rod are covered with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is `750K` in the steady state. The temperature of the surrounding air is `300K`. Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod. Stefan constant `sigma=6.0xx10^(-1)Wm^(-2)K^(-4)` .
View SolutionA solid copper sphere (density rho and specific heat c) of radius r at an initial temperature `200K` is suspended inside a chamber whose walls are at almost `0K.` The time required for the temperature of the sphere to drop to 100K is …….
View SolutionA body cools down from `50^(@)C` to `45^(@)C` in `5` minutes and to `40^(@)C` in another `8` minutes. Find the temperature of the surrounding.
View SolutionThe temperature of a body falls from `40^(@)C` to `30^(@)C` in 10 min when placed in a surrounding of constant temperature `15^(@)C`. Find the time taken for the temperature of the body to becomes `20^(@)C`
View SolutionA calorimeter contains `10 g` of water at `20^(@)C`. The temperature falls to `15^(@)C` in 10 min. When calorimeter contains `20 g` of water at `20^(@)C`, it takes 15 min for the temperature to become `15^(@)C`. Find the water equivalent of the calorimeter.
View SolutionA metal ball of mass `1kg` is heated by means of a `20W` heater in a room at `20^(@)C` . The temperature of the ball becomes steady at `50^(@)C` . (a) Find the rate of loss of heat to the surrounding when the ball is at `50^(@)C` . (b) Assuming Newton's law of cooling, calculate the rate of loss of heat to the surrounding when the ball is at `30^(@)C` . (c) Assume that the temperature of the ball rises uniformly from `20^(@)C` to `30^(@)C` in `5` minutes. Find the total loss of heat to the surrounding during this period. (d) Calculate the specific heat capacity of the metal.
View SolutionA hot body placed in a surrounding of temperature `theta_(0)` obeys Newtons's law of cooling `d theta // dt = - k (theta - theta_(0))`. Its temperature at `t = 0` is `theta_(1)`. The specific heat capacity of the body is `s` and its mass is`m`.
Find
(a) the maximum heat that the body can lose and
(b) the time starting from `t = 0` in which it will lose `90%` of this maximum heat.
View SolutionTwo bodies `A` and `B` have thermal emissivities of 0.01 and 0.081 respectively. The outer surface areas of the two bodies are same. The two bodies emit total radiant power at the same rate. The wavelength `lambda_(B)` corresponding to maximum spectral radiancy in the radiation from `B` is shifted radiancy in the radiation from `A` by `1.00 mu m`. If the temperature of `A` is `5802 K`, calculate
(a) the temperature of `B` and
(b) wavelength `lambda_(B)`
View Solution
Example questions and complete solutions for chapter HEAT TRANSFER of CP SINGH PHYSICS (HINGLISH) of Class 11