Complete Solutions to Solved Example of chapter MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION |
| DC PANDEY NEET | Solved Example |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A particle moves in a plane such that its coordinates changes with time as `x = at` and `y = bt`, where a and b are constants. Find the position vector of the particle and its direction at any time t.
View SolutionAn object moves from position (3,4) to (6,5) in the xy-plane. Find the magnitude and direction of displacement vector of the particle.
View SolutionA particle moves in xy-plane from position (1m,2m) to (3m,4m) in 2s. Find the magnitude and direction of average velocity.
View SolutionPosition vector of a particle is given as
`r = 2t hati +3t^(2) hatj` where t is in second and the coefficients have the proper units, for r to be in metres.
(i) Find instantaneous velocity v(t) of the particle.
(ii) Find magnitude and direction of v(t) at `t = 2s`
View SolutionVelocity of a particle changes from `(3hati +4hatj)m//s` to `(6hati +5hatj)m//s` 2s. Find magnitude and direction of average acceleration.
View SolutionThe position of a particle is given by
`r = 3t hati +2t^(2) hatj +8 hatk`
where, t is in seconds and the coefficients have the proper units for r to be in metres.
(i) Find v (t) and a(t) of the particles.
(ii) Find the magnitude and direction of v(t) and a(t) at `t = 1s`.
View SolutionA particle starts from origin at `t = 0` with a velocity of `15 hati ms^(-1)` and moves in xy-plane under the action of a force which produces a constant acceleration of `15 hati + 20 hatj ms^(-2)`. Find the y-coordinate of the particle at the instant its x-coordinate is 180 m.
View SolutionAn object has a velocity, `v = (2hati + 4hatj) ms^(-1)` at time `t = 0s`. It undergoes a constant acceleration `a = (hati - 3hatj)ms^(-2)` for 4s. Then
(i) Find the coordinates of the object if it is at origin at `t = 0`
(ii) Find the magnitude of its velocity at the end of 4s.
View SolutionA body is projected with a velocity of `20 ms^(-1)` in a direction making an angle of `60^(@)` with the horizontal. Determine its (i) position after 0.5 s and (ii) the velocity after `0.5s`.
View SolutionA stone is thrown with a speed of `10 ms^(-1)` at an angle of projection `60^(@)`. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take `g = 10 ms^(-2)`)
View SolutionA cricket ball is thrown at a speed of ` 28 ms^(-1)` in a direction `30 ^(@)` above the horizontal. Calculate (a)the maximum height (b) the time taken by ball to return to the same level, and (c )the distance from the thrower to the point where the ball returns to the same level.
View SolutionAssume that a ball is kicked at an angle of `60^(@)` with the horizontal, so if the horizontal component of its velocity is `19.6 ms^(-1)`, determine its maximum height.
View SolutionAn object is projected with a velocity of `30 ms^(-1)` at an angle of `60^(@)` with the horizontal. Determine the horizontal range covered by the object.
View SolutionA projectile has a range of `40 m` and reaches a maximum height of `10 m`. Find the angle at which the projectile is fired.
View SolutionFind the angle of projection of a porjectile for which for horizontal range and maximum height are equal.
View SolutionThere are two angles of projection for which the horizontal range is the same. Show that the sum of the maximum heights for these two angles is independent of the angle of projection.
View SolutionProve that the maximum horizontal range is four times the maximum height attained by the projectile, when fired at an inclination so as to have maximum horizontal range.
View SolutionA football is kicked at an angle of `30^(@)` with the vertical, so if the horizontal component of its velocity is `20 ms^(-1)`, determine its maximum height.
View SolutionA bomb is released from an aeroplane flying at a speed of `720 km//h` in the horizontal direction `8000 m` above the ground. At what horizontal distance from the initial position of areoplane it strikes the ground.
View SolutionA body is thrown horizontally from the top of a tower and strikes the ground after three seconds at an angle of `45^@` with the horizontal. Find the height of the tower and the speed with which the body was projected. (Take ` g = 9.8 m//s^2`)
View SolutionA body is thrown horizontally from the top of a tower and strikes the ground after three seconds at an angle of `45^(@)` with the horizontal. Then find
(i) the height of the tower
(ii) the speed of projection of the body
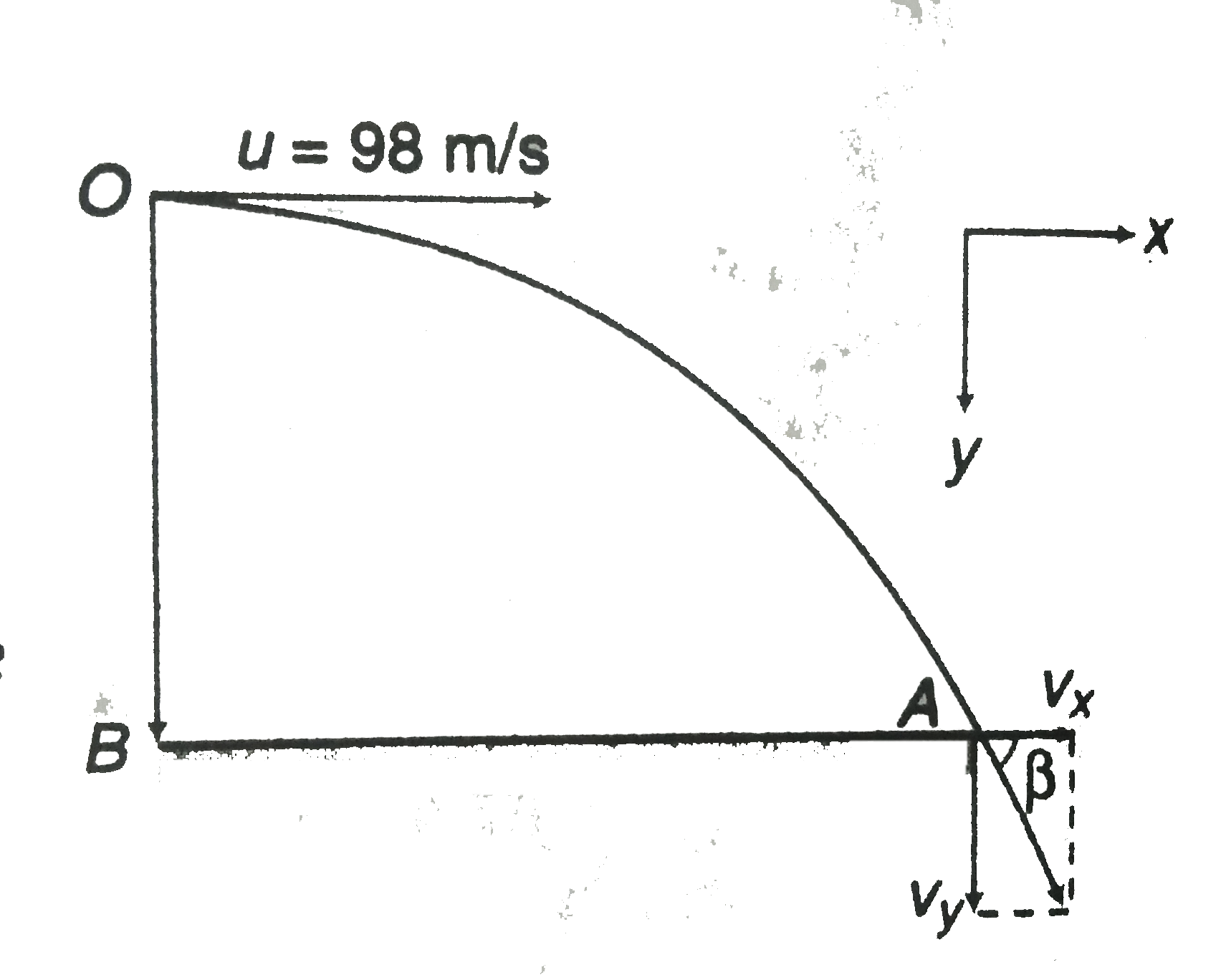
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. `(g= 9.8 m//s^2)`
 .
.
View SolutionA boy playing on the roof of a `10 m` high building throws a ball with a speed of `10 m//s` at an angle of `30^(@)` with the horizontal. How far from the throwing point will the ball be at the height of `10 m` from the ground ?
`[ g = 10m//s^(2) , sin 30^(@) = (1)/(2) , cos 30^(@) = (sqrt(3))/(2)]`
View SolutionA boy standing on the top of a tower 36 m high has a throw a packet to his friend standing on the ground 48 m horizontally away. If he throws a packet directly aiming the friend with a speed of `10 ms^(-1)`, how short will be packet fall ?
View Solution
Solved Example questions and complete solutions for chapter MOTION of DC PANDEY ENGLISH of Class 11