Complete Solutions to Taking it together of chapter MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION |
| DC PANDEY NEET | Taking it together |
| Number Of Questions | 96 |
| Academic Year | 2023-24 |
In a two dimensional motion,instantaneous speed `v_(0)` is a positive constant.Then which of the following are necessarily true?
View SolutionA particle velocity changes from `(2 hati - 3hatj) ms^(-1)` to `(3hati - 2hatj) ms^(-1)` in 2s. If its mass is 1kg, the acceleraton `(ms^(-2))` is
View SolutionFigure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to the initial horizontal velocity component, highest first.
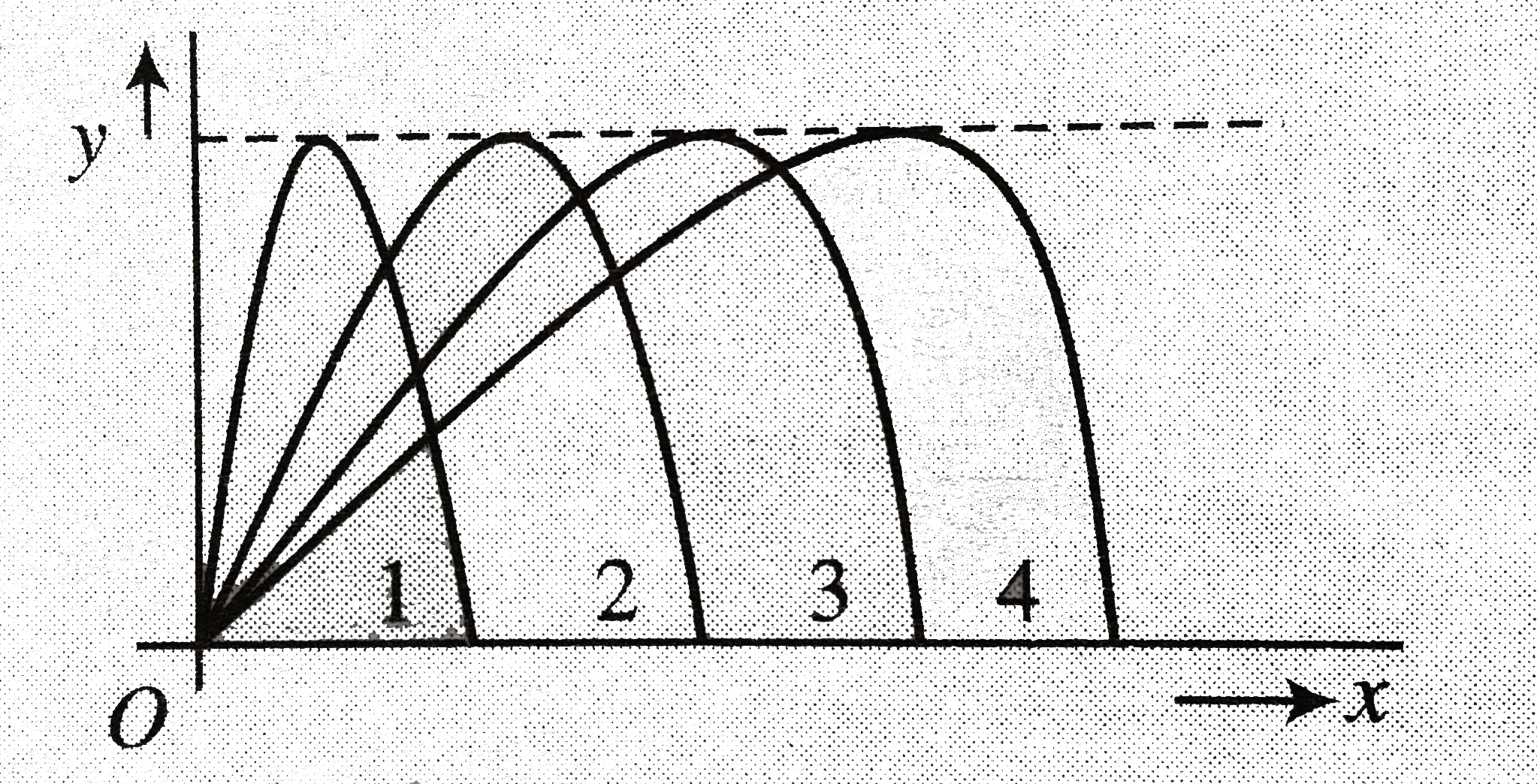 .
.
View SolutionWhich of the following is the graph between the height (h) of a projectile and time (t), when it is projected from the ground
View SolutionWhich of the following is the altitude-time graph for a projectile thrown horizontally from the top of the tower
View SolutionTwo projectiles `A` and `B` are thrown from the same point with velocities `v` and `v/2` respectively. If `B` is thrown at an angle `45^(@)` with horizontal.What is the inclination of `A`.when their ranges are the same?
View SolutionTwo stones having different masses `m_(1)` and `m_(2)` are projected at an angle `alpha` and `(90^(@) - alpha)` with same speed from same point. The ratio of their maximum heights is
View SolutionA projectile is thrown at an angle `theta` with the horizontal and its range is `R_(1)`. It is then thrown at an angle `theta` with vertical anf the range is `R_(2)`, then
View SolutionThe range of a projectile launched at an angle of `15^(@)` with horizontal is 1.5km. The range of projectile when launched at an angle of `45^(@)` to the horizontal is
View SolutionA body is thrown horizontally from the top of a tower of height `5 m`. It touches the ground at a distance of `10 m` from the foot of the tower. Find the initial velocity of the body.
View SolutionVelocity and acceleration of a particle at some instant of time are `v = (3hati +4hatj) ms^(-1)` and `a =- (6hati +8hatj)ms^(-2)` respectively. At the same instant particle is at origin. Maximum x-coordinate of particle will be
View SolutionA particle moves in the XY-plane according to the law `x = kt, y = kt (1- alphat)`, where k and `alpha` are positive constants and t is time. The trajectory of the particle is
View SolutionA projectile is thrown upward with a velocity `v_(0)` at an angle `alpha` to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
View SolutionThe equation of trajectory of an oblique projectile `y = sqrt(3) x - (g x^(2))/(2)`. The angle of projection is
View SolutionThe maximum range of a gun on horizontal terrain is 1km. If `g = 10 ms^(-2)`, what must be the muzzle velocity of the shell ?
View SolutionTwo paper screens `A` and `B` are separated by a distance of `100m`. A bullet pierces `A` and `B`. The hole in `B` is `10 cm` below the hole in `A`. If the bullet is travelling horizontally at the time of hitting the screen `A`, calculate the velocity of the bullet when it hits the screen `A`. Neglect resistance of paper and air.
View SolutionA body is projected at an angle of `30^(@)` with the horizontal with momentum `P`.At its highest point the magnitude of the momentum is:
View SolutionThe maximum height attaine by a projectile is increased by ` 10%` by increasing its speed of projecton, without changing the angle of projection. What will the percentage increase in the horizontal range.
View SolutionA ball is thrown up with a certain velocity at anangle `theta` to the horizontal. The kinetic energy KE of the ball varies with horizontal displacements as:
View SolutionA ball is thrown at different angles with the same speed `u` and from the same points and it has same range in both the cases. If `y_1 and y_2` be the heights attained in the two cases, then find the value of `y_1 + y_2`.
View SolutionA projectile is fired from level ground at an angle `theta` above the horizontal. The elevation angle `phi` of the highest point as seen from the launch point is related to `theta` by the relation.
View SolutionA ball is thrown up with a certain velocity at angle `theta` to the horizontal. The kinetic energy varies with height h of the particle as:
View SolutionA body of mass m is thrown upwards at an angle `theta` with the horizontal with velocity v. While rising up the velocity of the mass after t second will be
View SolutionA projectile is thrown with an initial velocity of `(a hati + hatj) ms^(-1)`. If the range of the projectile is twice the maximum height reached by it, then
View SolutionA projectile thrown with a speed v at an angle `theta` has a range R on the surface of earth. For same v and `theta`, its range on the surface of moon will be
View SolutionThree balls of same masses are projected with equal speeds at angle `15^(@), 45^(@), 75^(@)`, and their ranges are respectively `R_(1),R_(2)` and `R_(3)`, then
View SolutionA man can thrown a stone such that it acquires maximum horizontal range 80 m. The maximum height to which it will rise for the same projectile in metre is
View SolutionThe ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is
View SolutionThe velocity at the maximum height of a projectile is half of its velocity of projection `u`. Its range on the horizontal plane is
View SolutionA projectile is thrown from a point in a horizontal plane such that the horizontal and vertical velocities are `9.8 ms^(-1)` and `19.6 ms^(-1)`. It will strike the plane after covering distance of
View SolutionA stone is projected in air. Its time of flight is 3s and range is 150m. Maximum height reached by the stone is (Take, `g = 10 ms^(-2))`
View SolutionThe greatest height to which a boy can throw a stone is (h). What will be the greatest distance on horizontal surface upto which the boy can throw the stone with the same speed ? Neglect the air friction.
View SolutionThe range of a projectile when launched at angle `theta` is same as when launched at angle `2theta`. What is the value of `theta` ?
View SolutionA boy throws a ball with a velocity u at an angle `theta` with the horizontal. At the same instant he starts running with uniform velocity to catch the ball before it hits the ground. To achieve this he should run with a velocity of
View SolutionFor angles of projection of a projectile at angle `(45^(@) - theta) and (45^(@)+ theta)`, the horizontal ranges described by the projectile are in the ratio of :
View SolutionThe time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [`g=10 m//s^(2)`]
View SolutionFour bodies A,B,C and D are projected with equal velocities having angles of projection `15^(@),30^(@),45^(@) and 60^(@)` with the horizontal respectively. The body having the shortest range is
View SolutionA stone is thrown at an angle `theta` to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
View SolutionFor a given velocity, a projectile has the same range R for two angles of projection. If `t_(1)` and `t_(2)` are the time of flight in the two cases, then `t_(1)*t_(2)` is equal to
View SolutionTwo particles are projected obliquely from ground with same speed such that their range `'R'` are same but they attain different maximum heights `h_(1)` and `h_(2)` then relation between `R, h_(1)` and `h_(2)` is:
View SolutionA cricket ball is hit for a six the bat at an angle of `45^(@)` to the horizontal with kinetic energy K. At the highest point, the kinetic energy of the ball is
View SolutionThe equation of motion of a projectile is `y = 12 x - (3)/(4) x^2`. The horizontal component of velocity is `3 ms^-1`. What is the range of the projectile ?
View SolutionA particle is thrown with a speed u at an angle ` theta` with the horizontal. When the particle makes an angle `phi` with the horizontal. Its speed changes to v :
View SolutionA particle is projected in `x-y` plane with `y-`axis along vertical, the point of projection being origin. The equation of projectile is `y = sqrt(3) x - (gx^(2))/(2)`. The angle of projectile is ……………..and initial velocity is ………………… .
View SolutionA ball of mass m is projected from the ground with an initial velocity u making an angle of `theta` with the vertical. What is the change in velocity between the point of projection and the highest point ?
View SolutionA ball is projected form ground with a speed of `20 ms^(-1)` at an angle of 45∘ with horizontal.There is a wall of 25m height at a distance of 10m from the projection point. The ball will hit the wall at a height.
View SolutionA particle (A) is dropped from a height and another particles (B) is thrown into horizontal direction with speed of 5m/s sec from the same height. The correct statement is
View SolutionA bullet is to be fired with a speed of `2000 m//s` to hit a target `200 m` away on a level ground. If `g = 10 m//s^(2)`, the gun should be aimed
View SolutionAn aeroplane moving horizontally with a speed of `720 km//h` drops a food pocket, while flying at a height of 396.9 m . the time taken by a food pocket to reach the ground and its horizontal range is (Take `g = 9.8 m//sec`)
View SolutionA boy can throw a stone up to a maximum height of `10 m`. The maximum horizontal distance that the boy can throw the same stone up to will be :
View SolutionAt the height 80 m , an aeroplane is moving with `150 m//s` . A bomb is dropped from it so as to hit a target. At what distance from the target should the bomb be dropped (given `g = 10 m//s`)
View SolutionA particle moves along a parabolic path `y=-9x^(2)` in such a way that the `x` component of velocity remains constant and has a value `1/3m//s`. Find the instantaneous acceleration of the projectile (in `m//s^(2)`)
View SolutionThe maximum range of a projectile is 500m. If the particle is thrown up a plane, which is inclined at an angle of `30^@` with the same speed, the distance covered by it along the inclined plane will be
View SolutionA ball is thrown from a point O aiming a target at angle `30^(@)` with the horizontal so that the ball hits the target at B but the ball hits at point A, a vertical distance h below B. If the intial velocity of the ball is `20 ms^(-1)` and the horizontal distance between O and C is 10 m. Find the value of h.

View SolutionThe range of a projectile fired at an angle of `15^@` is 50 m. If it is fired with the same speed at an angle of `45^@` its range will be
View SolutionA cricket fielder can throw the cricket ball with a speed `v_(0)`.If the throws the ball while running with speed `u` at an angle `theta` to the horizontal.
The effective angle to the horizontal at which the ball is projected in air as seen by a spectator is
View SolutionTwo stones are projected so as to reach the same distance from the point of projection on a horizontal surface. The maximum height reached by one exceeds thr other by an amount equal to half the sum of the height attained by them. Then angle of projection of the stone which attains smaller height is
View SolutionA projectile A is thrown at an angle `30^(@)` to the horizontal from point P. At the same time, another projectile B is thrown with velocity `v_(2)` upwards from the point Q vertically below the highest point A would reach. For B to collide with A the ratio `(v_(2))/(v_(1))` should be

View SolutionThe equations of motion of a projectile are given by `x=36t m and 2y =96t-9.8t^(2)m`. The angle of projection is
View SolutionA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of `theta` . From the same point and at the same instant , a person starts running with a constant speed `('v_(0)')/(2) ` to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection `theta` ?
View SolutionAn arrow is shot into air. Its range is 200m and its time of flight is 5s. If `g = 10ms^(-2)`, then horizontal component of velocity and the maximum height will be respectively
View SolutionA particle of mass 2kg moves with an initial velocity of `vec(v)=4hat(i) +4hat(j) ms^(-1)`. A constant force of `vec(F) =20hat(j)N` is applied on the particle. Initially, the particle was at (0,0). The x-coordinates of the particle when its y-coordinates again becomes zero is given by
View SolutionTwo balls are thrown simultaneously from ground with same velocity of `10 ms^(-1)` but different angles of projection with horizontally. Both balls fall at same distance `5sqrt(3)m` from point of projection. What is the time interval between balls striking the ground ?
View SolutionA piece of marble is projected from earth's surface with velocity of `19.6 sqrt(2) ms^(-1)` at `45^(@)`. 2 s later its velocity makes an angle `alpha` with horizontal, where `alpha` is
View SolutionAn object of mass m is projected with a momentum p at such an angle that its maximum height is `1//4` th of its horizontal range. Its minimum kinetic energy in its path will be
View SolutionA particle is projected with a velocity of `30 ms^(-1)`, at an angle of `theta_(0) = tan^(-1) ((3)/(4))`. After 1s, the particle is moving at an angle `theta` to the horizontal, where `tan theta` will be equal to (Take, `g = 10 ms^(-2))`
View SolutionA body is projected from the ground with a velocity `v = (3hati +10 hatj)ms^(-1)`. The maximum height attained and the range of the body respectively are (given `g = 10 ms^(-2))`
View SolutionA bomber moving horizontally with `500m//s` drops a bomb which strikes ground in 10s. The angle of strike with horizontal is
View SolutionA ball rolls off the edge of a horizontal table top 4 m high. If it strikes the floor at a point 5 m horizontally away from the edge of the table, what was its speed at the instant it left the table?
View SolutionA ball is projected upwards from the top of a tower with a velocity `50ms^-1` making an angle `30^@` with the horizontal. The height of tower is 70m. After how many seconds from the instant of throwing, will the ball reach the ground. `(g=10 ms^-2)`
View SolutionFrom the top of tower of height 40 m a ball is projected upwards with a speed of 20 m/sec at an angle of elevation of `30^(@).` Then the ration of the total time taken by the ball to hit the ground to its time of flight ( time taken to come back to the same elevation) is ( take `g = 10 m//sec ^(2))`
View SolutionThe coordinates of a moving particle at any time t are given by `x = ct` and `y = bt^(2)`. The speed of the particle is given by
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed `(2v)/(sqrt(3))`. If particle B hits the particle A, the angle of projection of B with the vertical is
View SolutionAn object is projected with a velocity of `20(m)/(s)` making an angle of `45^@` with horizontal. The equation for the trajectory is `h=Ax-Bx^2` where h is height, x is horizontal distance, A and B are constants. The ratio A:B is (g`=ms^-2)`
View SolutionA particle is projected from horizontal making an angle of `53^(@)` with initial velocity `100 ms^(-1)`. The time taken by the particle to make angle `45^(@)` from horizontal is
View SolutionLet A, B and C be points in a vertical line at height h, `(4h)/(5) and (h)/(5) ` and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is ` T_(BC) ` . Then ` (T)/(T_(BC)) ^(2) = `
View SolutionA particle is projected form a horizontal plane `(x-z` plane) such that its velocity vector at time `t` is gives by `vecV = ahati +(b - ct)hatj`. Its range on the horizontal plane is given by
View SolutionA ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
View SolutionThe horizontal range and miximum height attained by a projectile are `R and H`, respectively. If a constant horizontal acceleration `a = g//4` is imparted to the projectile due to wind, then its horizontal range and maximum height will be
View SolutionA large number of bullets are fired in all directions with the same speed `v`. Find the maximum area on the ground on which these bullets will spread.
View SolutionA cart is moving horizontally along a straight line with constant speed `30 ms^-1.` A particle is to be fired vertically upwards from the moving cart in such a way that it returns to the cart at the same point from where it was projected after the cart has moved `80 m.` At what speed (relative to the cart) must the projectile be fired? (Take `g = 10 ms^-2`)
View SolutionA particle is projected from the ground at an angle `30^@` with the horizontal with an initial speed `20 m s^-1`. After how much time will the velocity vector of projectile be perpendicular to the initial velocity ? [in second].
View SolutionTwo particles are simultaneously projected in opposite directions horizontally from a given point in space where gravity g is uniform. If `u_(1)` and `u_(2)` be their initial speeds, then the time t after which their velocitites are mutually perpendicular is given by
View SolutionA hill is ` 500 m` high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of `125 m//s` over the hill . The canon is located at a distance of ` 800 m` from the foot to hill and can be moved on the ground at a speed of `2 m//s` , so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach on the ground across the hill ? Take ` g= 10 m//s^2`.
View SolutionA ball is rolled off the edge of a horizontal table at a speed of `4 m//"second"`. It hits the ground after 0.4 second . Which statement given below is true
View SolutionA jet aeroplane is flying at a constant height of 2 km with a speed `360 kmh^(-1)` above the ground towards a target and releases a bomb. After how much time it will hit the target and what will be the horizontal distance of the aeroplane from the target so that the bomb should hit the target ? (Take `g = 10 ms^(-2))`
View SolutionTwo seconds after projection, a projectile is travelling in a direction inclined at `30^@` to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of its velocity.
View SolutionA projectile is fired at an angle of `30^(@)` to the horizontal such that the vertical component of its initial velocity is `80m//s`. Its time of fight is `T`. Its velocity at `t=T//4` has a magnitude of nearly.
View SolutionA very broad elevator is going up vertically with constant acceleration of `2" m/s"^(2)`. At the instant when its velocity is 4 m/s a ball is projected from the floor of the lift with a speed of 4 m/s relative to the floor at an elevation of `30^(@)`. The range of ball over the floor of the lift is :
View SolutionThe velocity of a projectile when it is at the greatest height is `(sqrt (2//5))` times its velocity when it is at half of its greatest height. Determine its angle of projection.
View SolutionA body of mass 1kg is projected with velocity `50 ms^(-1)` at an angle of `30^(@)` with the horizontal. At the highest point of its path a force 10 N starts acting on body for 5s vertically upward besids gravitational force, what is horizontal range of the body (Take, `g = 10 ms^(-2))`
View SolutionA grasshopper can jump a maximum distance of `1.6 m`. It spends negligible time on the ground. How far can it go in `10 s` ?
View SolutionA ball rolls off the top of a staircase with a horizontal velocity `u m//s`. If the steps are h meter high and b meter wide, the ball will hit the edge of the nth steps, if:
View SolutionIn the given figure for a projectile

View SolutionTwo particles projected form the same point with same speed u at angles of projection `alpha and beta` strike the horizontal ground at the same point. If `h_1 and h_2` are the maximum heights attained by the projectile, R is the range for both and `t_1 and t_2` are their times of flights, respectively, then incorrect option is :
View SolutionBalls A and B are thrown form two points lying on the same horizontal plane separated by a distance 120 m. which of the following statemet (s) is/are correct ?
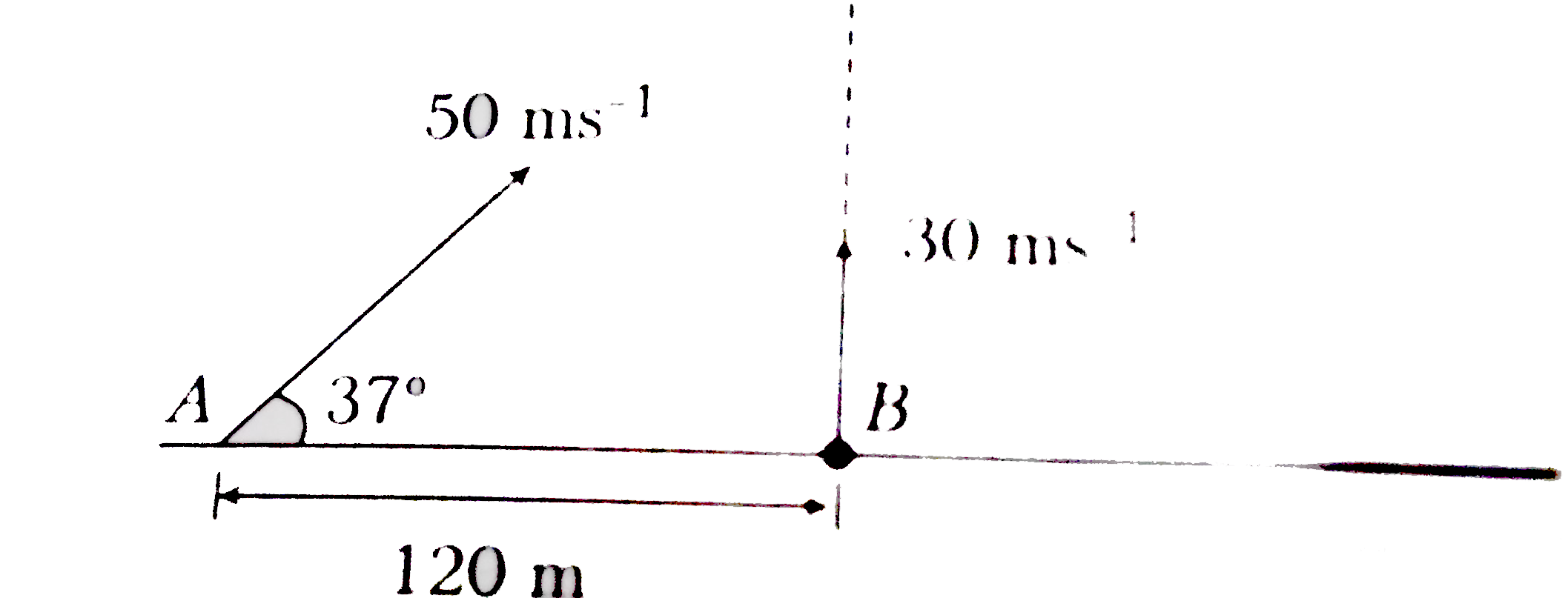
View Solution
Taking it together questions and complete solutions for chapter MOTION of DC PANDEY ENGLISH of Class 11