Complete Solutions to Level - 1 Subjective of chapter PROJECTILE MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROJECTILE MOTION |
| DC PANDEY | Level - 1 Subjective |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
At time `t=0`, a small ball is projected from point A with a velocity of `60m//s` at `60^@` angle with horizontal. Neglect atmospheric resistance and determine the two times `t_1 and t_2` when the velocity of the ball makes an angle of `45^@` with horizontal x-axis.
View SolutionA particle is projected from ground with velocity `20(sqrt2) m//s` at `45^@`. At what time particle is at height 15 m from ground? `(g = 10 m//s^2)`
View SolutionA particle is projected at an angle `60^@` with horizontal with a speed `v = 20 m//s`. Taking `g = 10m//s^2`. Find the time after which the speed of the particle remains half of its initial speed.
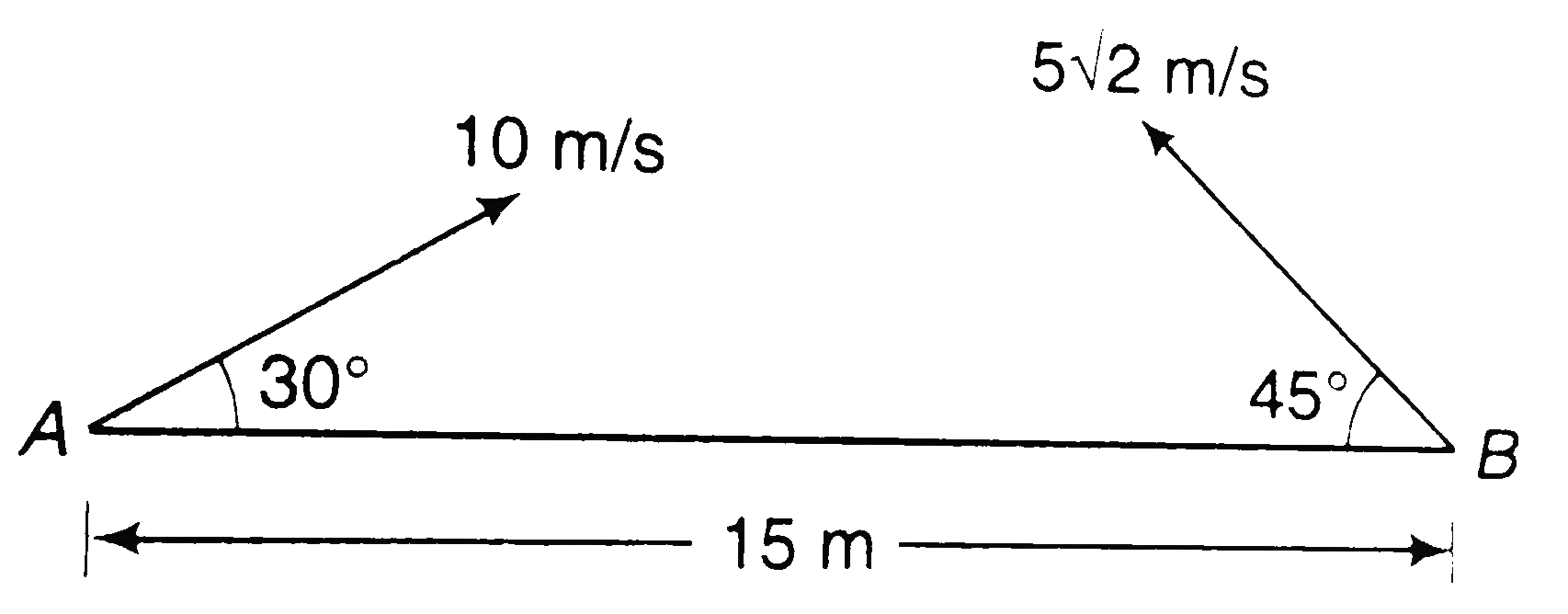
View SolutionTwo particles A and B are projected from ground towards each other with speeds `10 m//s` and `5(sqrt2) m//s` at the angle `30^@ and 45^@` with horizontal from two points separated by a distance of 15 m.
will they collide or not ?
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities `v_1 = 3m//s and v_2= 4m//s` horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
View SolutionA ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
View SolutionA body is projected up such that its position vector varies with time as `r = { 3thati + (4 t - 5t^2)hatj}` m. Here, t is in seconds. Find the time and x-coordinate of particle when its y-coordinate is zero.
View SolutionA particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? `(g = 10 m/s^2)`

View SolutionIn the above problem, what is the component of its velocity perpendicular to the plane when it strikes at A ?
View SolutionTwo particles A and B are projected simultaneously from two towers of heights 10 m and 20m respectively. Particle A is projected with an initial speed of `10 sqrt(2) m//s` at an angle of `45^@` with horizontal, while particle B is projected horizontally with speed `10 m//s`. If they collide in air, what is the distance d between the towers?
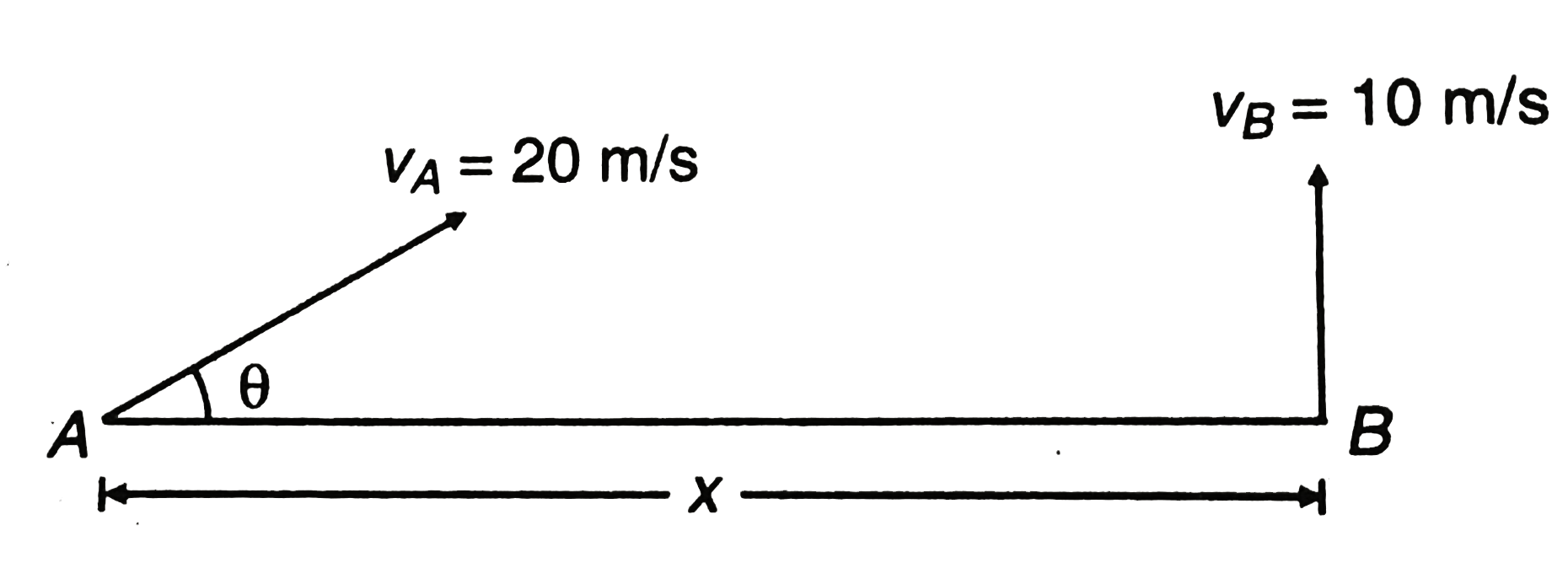
View SolutionA particle is projected from the bottom of an inclined plane of inclination `30^@` with velocity of `40 m//s` at an angle of `60^@` with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take `g = 10 m//s^2`.
View SolutionTwo particles A and B are projected simultaneously in the directins shown in figure with velocities `v_(A) = 20 m//s and v_(B) = 10 m//s` respectively. They collide in air after `1/2` s. Find
(a) the angle `theta`
(b) the distance x.
 .
.
View SolutionA ball is shot from the ground into the air. At a height of 9.1 m, its velocity is observed to be `v = 7.6 hati + 6.1 hatj` in metre per second (`hati` is horizontal, `hatj` is upward). Give the approximate answers.
(a) To what maximum height does the ball rise?
(b) What total horizontal distance does the ball travel?
(c) What are the magnitude and
(d) What are the direction of the ball's velocity just before it hits the ground?
View SolutionA particle is projected with velocity `2 sqrt(gh)` so that it just clears two walls of equal height h which are at a distance 2h from each other. Show that the time of passing between the walls is `2 sqrt(h//g)`.
View SolutionA particle is projected at an angle of elevation `alpha` and after t second it appears to have an elevation of `beta` as seen from the point of projection. Find the initial velocity of projection.
View SolutionA projectile aimed at a mark, which is in the horizontal plane through the point of projection, falls a cm short of it when the elevation is `alpha` and goes b cm far when the elevation is `beta`. Show that, if the speed of projection is same in all the cases the proper elevation is
`1/2 sin^(-1) [(bsin2alpha+asin2beta)/(a+b)]` .
View SolutionTwo particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are `v_1= 5m//s and v_2 = 7.5 m//s` respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water.
View SolutionA ballon is ascending at the rate `v = 12 km//h` and is being carried horizontally by the wind at `v_(w) = 20 km//h`. If a ballast bag is dropped from the balloon at the instant h = 50 m, determine the time needed for it to strike the ground. Assume that the bag was released from the ballon with the same velocity as the balloon. Also, find the speed with which the bag strikes the ground?
View SolutionA projectile is fired with a velocity u at right angles to the slope, which is inclined at an angle `theta` with the horizontal. Derive an expression for the distance R to the point of impact.
 .
.
View SolutionAn elecator is going up with an upward acceleration of `1m//s^2`. At the instant when its velocity is `2 m//s`, a stone is projected upward from its floor with a speed of `2m//s` relative to the elevator, at an elevation of `30^@`.
(a) Calculate the time taken by the stone to return to the floor.
(b) Sketch the path of the projectile as observed by an observer outside the elevator.
(c) If the elevator was moving with a downward acceleration equal to g, how would the motion be altered?
View SolutionTwo particles A and B are projected simultaneously in a vertical plane as shown in figure. They collide at time t in air. Write down two necessary equations for collision to take place.

View Solution
Level - 1 Subjective questions and complete solutions for chapter PROJECTILE MOTION of DC PANDEY ENGLISH of Class 11