Complete Solutions to MCQ_TYPE of chapter KINEMATICS 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS 1 |
| DC PANDEY MASTER PROBLEM PACKAGE | MCQ_TYPE |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
Velocity displacement graph of a particle moving in a straight line is as shown in figure.
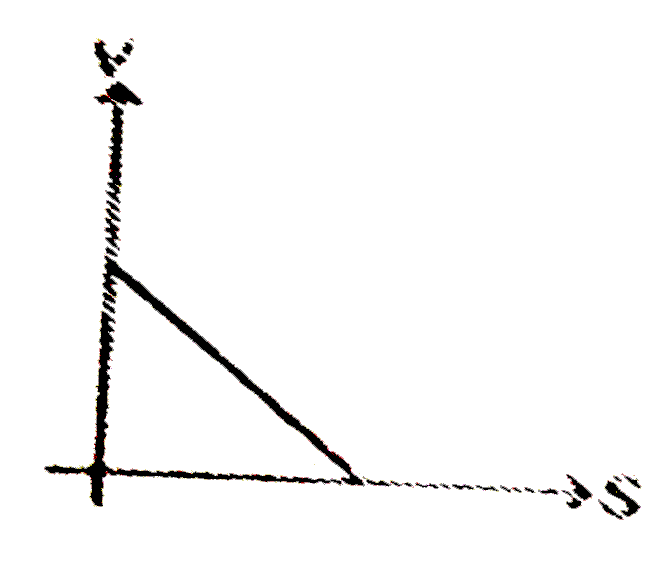 08:23View Solution
08:23View SolutionLet `v` and `a` be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed `(dv)/(dt)` of the particle is equal to
02:04View SolutionStarting from rest a particle is first accelerated for time `t_1` with constant acceleration `a_1` and then stops in time `t_2` with constant retardation `a_2.` Let `v_1` be the average velocity in this case and `s_1` the total displacement. In the second case it is accelerating for the same time `t_1` with constant acceleration `2a_1` and come to rest with constant retardation `a_2` in time `t_3.` If `v_2` is the average velocity in this case and `s_2` the total displacement, then
11:39View SolutionA particle leaves the origin with an initial velodty `v= (3.00 hati) m//s` and a constant acceleration `a= (-1.00 hati-0.500 hatj) m//s^2.` When the particle reaches its maximum x coordinate, what are
(a) its velocity and (b) its position vector?04:45View SolutionAcceleration of a particle which is at rest at ` x=0 ` is `vec a = (4 -2 x) hat i`. Select the correct alternative (s).
04:00View SolutionA car is moving rectilinearly on a horizontal path with acceleration `a_(0)`.A person sitting inside the car observes that an insect `S` is crawling up the screen with an acceleration a.If `theta` is the inclination of the wind screen with the horizontal, then the acceleration of the insect.
03:56View SolutionThe coordinate of a particle moving in a plane are given by ` x(t) = a cos (pt) and y(t) = b sin (pt)` where `a,b (lt a)` and `P` are positive constants of appropriate dimensions . Then
11:23View Solutiona particle moving along a straight line with uniform acceleration has velocities `7 m//s` at A and `17 m//s` at C. B is the mid point of AC. Then :-
06:49View SolutionLet `r` be the radius vector of a particle in motion about some reference point and `r` its modulus. Similarly, `v` be the velocity vector and `v` its modulus. Then
01:31View SolutionTwo particles `A` and `B` are located in `x-y` plane at points `(0,0)` and `(0,4m)`. They simultaneoulsy start moving with velocities `v_(A)=2hatjm//s` and `v_(B)=2hatim//s`. Select the correct alternative(s)
08:57View SolutionThe co-ordinate of the particle in x-y plane are given as `x=2+2t+4t^(2)` and `y=4t+8t^(2)` :-
The motion of the particle is :-04:08View SolutionRiver is flowing with a velocity `v_(BR)=4hatim//s`. A boat is moving with a velocity of `v_(BR)=(-2hati+4hatj)m//s` relative to river. The width of the river is `100m` along `y`-direction. Choose the correct alternative(s)
01:53View SolutionA particle is moving along `x`-axis. Its velocity `v` with `x` co-ordinate is varying as `v=sqrt(x)`. Then
02:59View SolutionFrom `v-t` graph shown in figure. We can draw the following conclusions
 02:09View Solution
02:09View SolutionA particle `P` is projected upwards with `80m//s`. One second later another particle `Q` is projected with initial velocity `70m//s`. Before either of the particle srikes the ground `(g=10m//s^(2))`
03:04View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
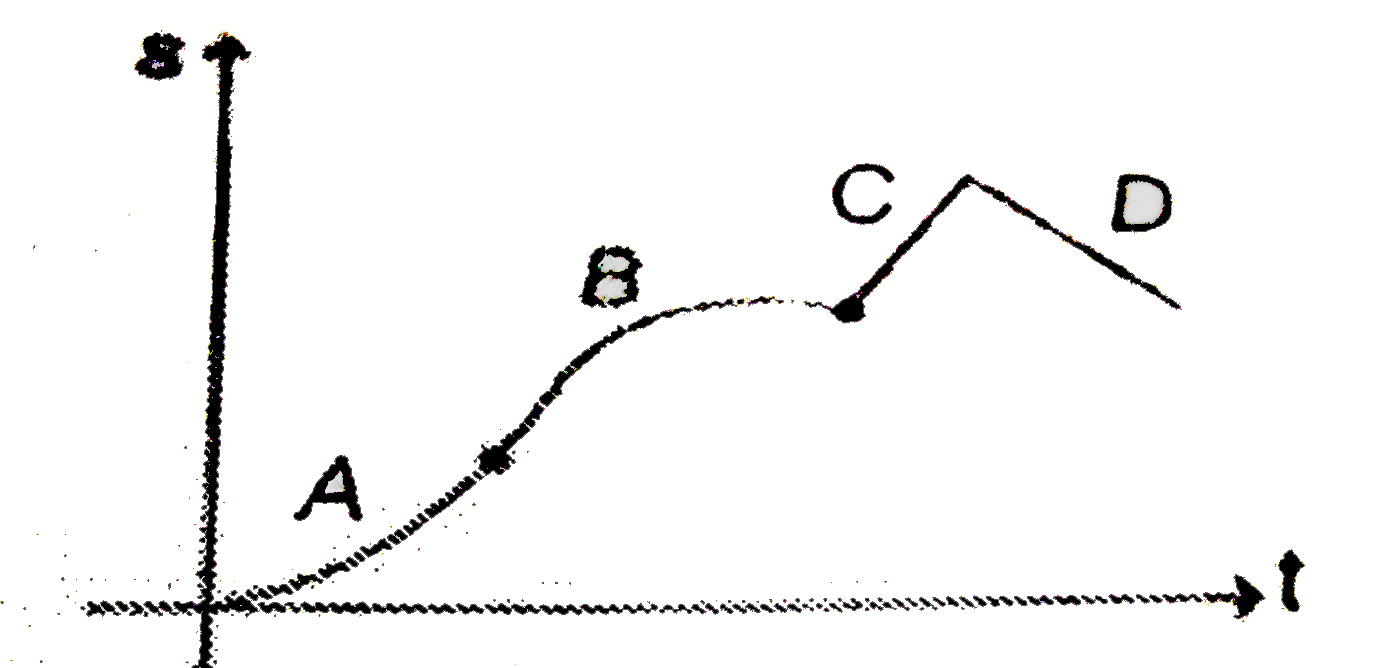 02:37View Solution
02:37View SolutionAt time `t=0`, a particle is at `(-1m, 2m)` and at `t=2s` it is at `(-4m,6m)`. From this we can conclude that in the given time interval.
02:36View SolutionA particle `P` lying on a smooth horizontal `x-y` plane starts from `(3hati+4hatj)m` with velocity `(2hati)m//s`. Another particle `Q` is projected (horizontally from origin with velocity `(xhati+yhatj)` so that is strikes `P` after `2s`. Then
01:59View SolutionPath of a particle moving in `x-y` plane is `y=3x+4`. At some instant suppose `x`- component of velocity is `1m//s` and it is increasing at a constant rate of `1m//s^(2)`. Then at this instant.
03:29View SolutionA particle moves along the X-axis as `x=u(t-2s)=at(t-2)^2`.
02:49View SolutionA man standing on the edge of the terrace of a high rise building throws a stone, vertically up with at speed of `20 m//s`. Two seconds later, an identical stone is thrown vertically downwards with the same speed of `20 m`,. Then
02:37View SolutionThe `v-t` graph for two particles `P` and `Q` are given in the figure. Consider the following statements(s). Then, which of the following statement(s) is/are True:
 02:24View Solution
02:24View SolutionA particle is moving in a straight line along the positive `x`-axis such that its speed is inversely proportional to the distance from origin `[vprop1/ximpliesv=k/x` where `k` is the proportionally constant].
The graph of motion of the particle for `1//v` versus `x` (distance from origin) is shown in the figure.
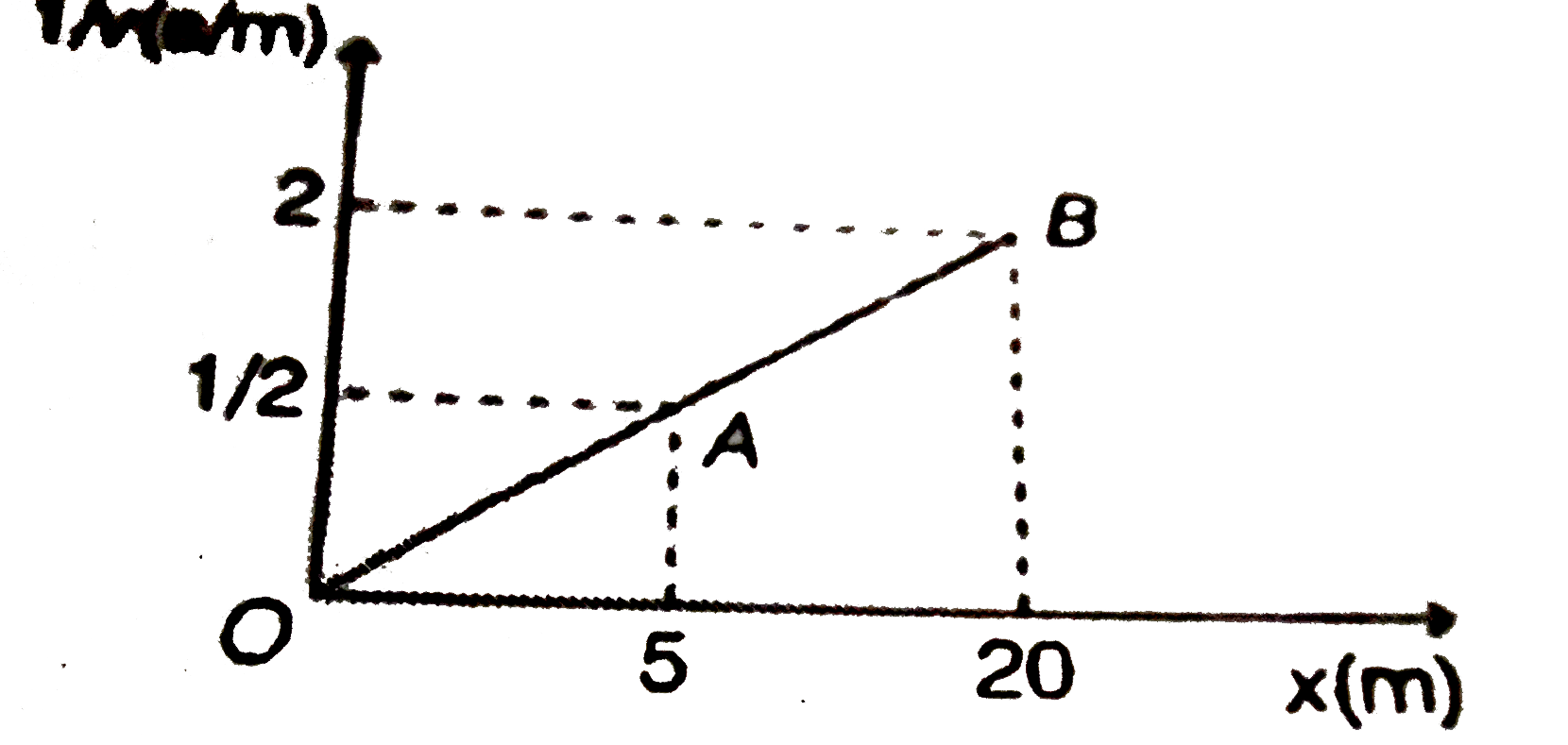 02:46View Solution
02:46View SolutionA subway train travels between two of its stations at then stops with the acceleration shcedule shown in the acceleration versus time graph. Then
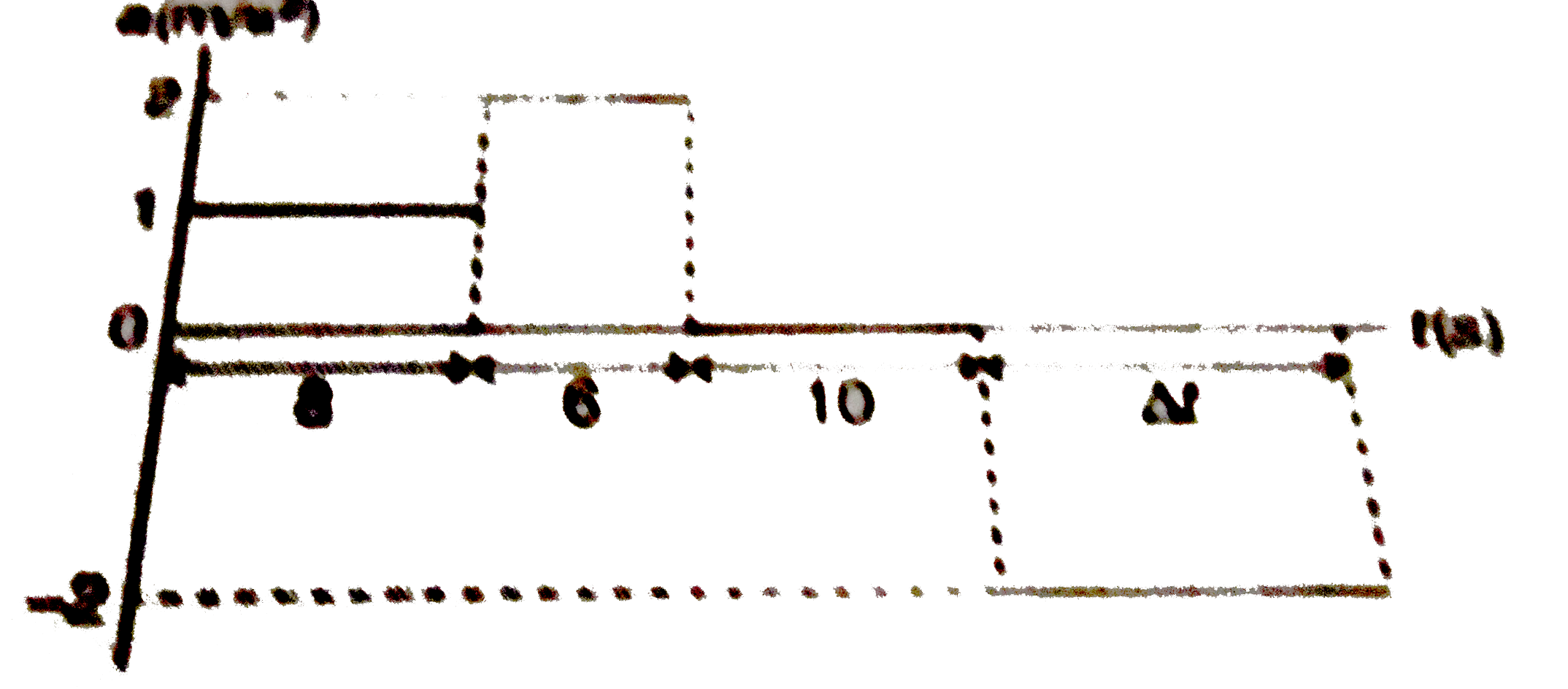 03:42View Solution
03:42View SolutionA particle starts moving with initial velocity `3m//s` along `x`- axis from origin. Its acceleration is varying with `x` co-ordinate in parobalic nature as shown in the figure. At `x=1m `, tangent to the graph makes an angle `45^(@)` with positive `x`- aixs. Then at `x=3m`,
 03:10View Solution
03:10View SolutionA train starts from rest at `S = 0` and is subjected to an acceleration as shown in figure. Then,
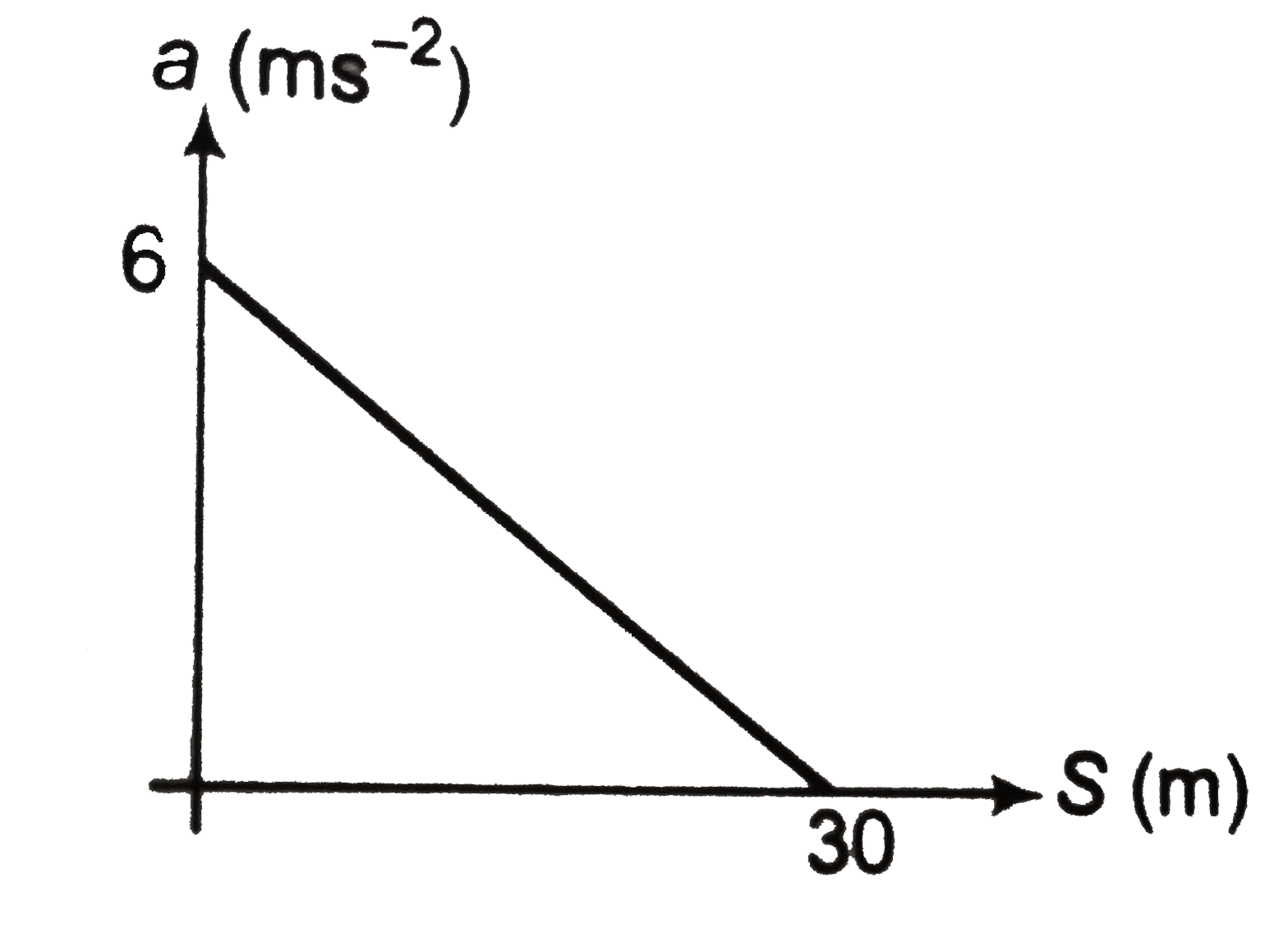 06:50View Solution
06:50View SolutionMan A is sitting in a car moving with a speed of 54 `(km)/(hr)` observes a man B in front of the car crossing perpendicularly a road of width 15 m in three seconds. Then the velocity of man B (in `(m)/(s)`) will be:
03:06View Solution
MCQ_TYPE questions and complete solutions for chapter KINEMATICS 1 of DC PANDEY PHYSICS (HINGLISH) of Class 11
