Complete Solutions to JEE Advanced of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | JEE Advanced |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
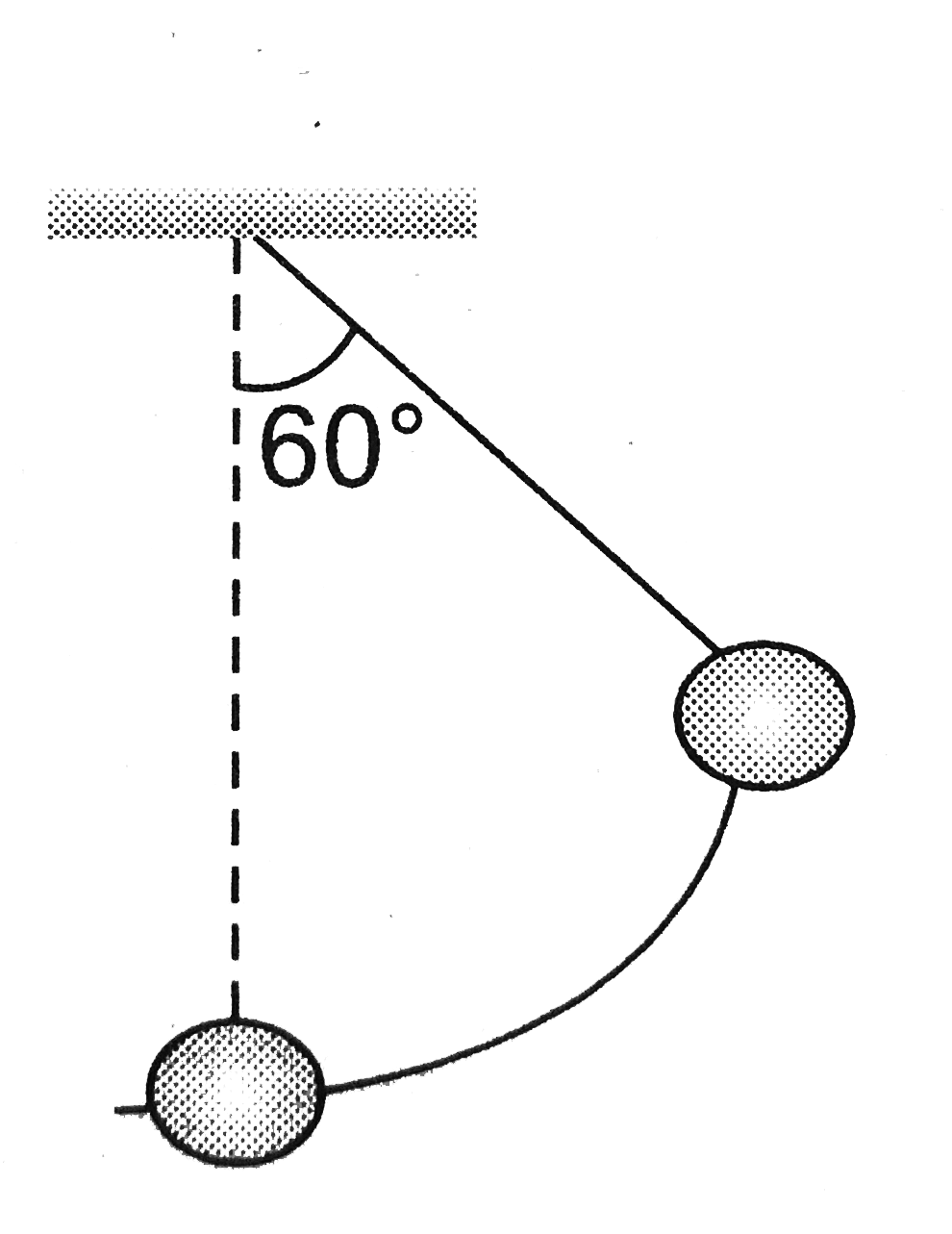
A pendulum of length `l=1m` is released from `theta_(0)=60^(@)` . The rate of change of speed of the bob at `theta=30^(@)` is.
View SolutionA particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
View SolutionA block of mass `m` is placed inside a smooth hollow cylinder of radius `R` kept horizontally. Initially system was at rest. Now cylinder is given constant acceleration `2 g` in the horizontal direction by external agent. Find the maximum angular displacement of the block with the vertical.
 .
.
View SolutionA simple pendulum is vibrating with an angular amplitude of `90^(@)` as shown in figure. For what value of `alpha` (angle between string and vertical) during its motion, the total acceleration is directed horizontally ?
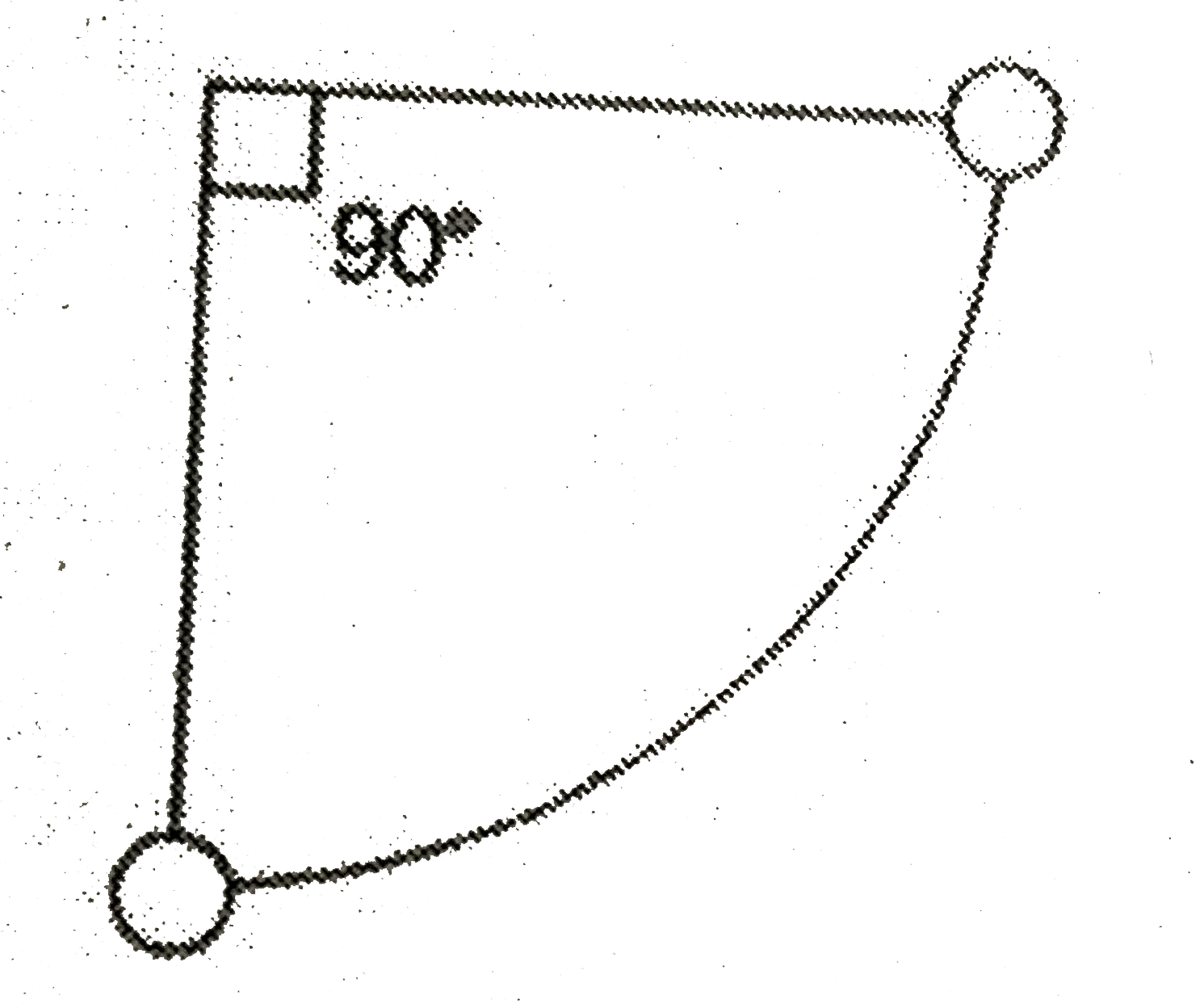
View SolutionA ball of mass `m` is attached to one end of a light rod of length `l`, the other end of which is hinged. What minimum velocity `v` should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionA particle is given an initial speed `u` inside a smooth spherical shell of radius `R=1` m such that it is just able to complete the circle. Acceleration of the particle when its velocity is vertical is

View SolutionA bob is suspended from a crane by a cable of length `l=5 m`. The crane and load are moving at a constant speed `v_(0)`. The crane is stopped by a bumper and the bob on the cable swings out an angle of `60^(@)`. The initial speed `v_(0)` is `(g=9.8 m//s^(2))`
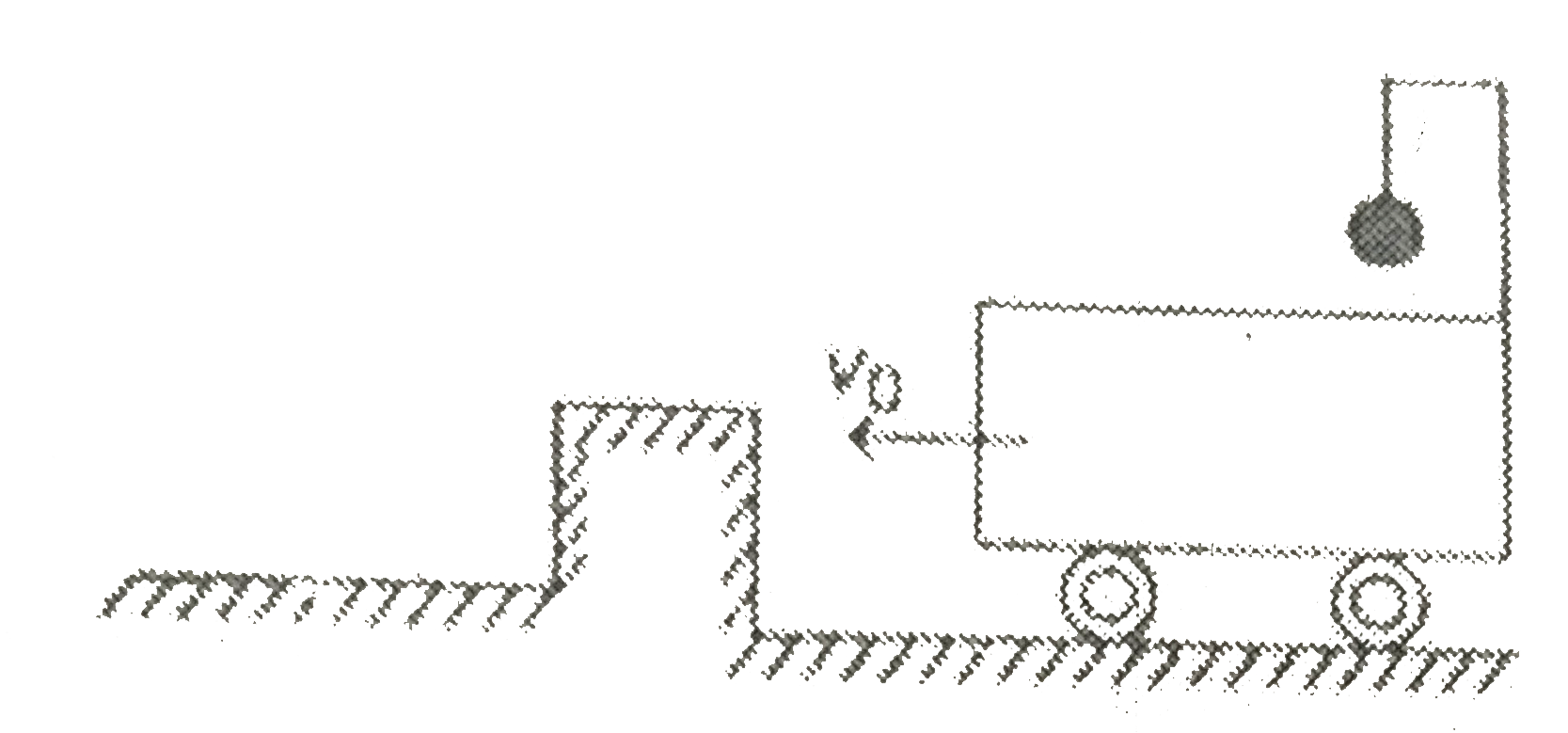
View SolutionA smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle `theta` it slides.
View SolutionTwo bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass `m` hanging from a string of length `l` is executing oscillations of angular amplitude `theta_(0)` while the other body is at rest. The minimum coefficient of friction between the mass `4m` and the horizontal surface should be
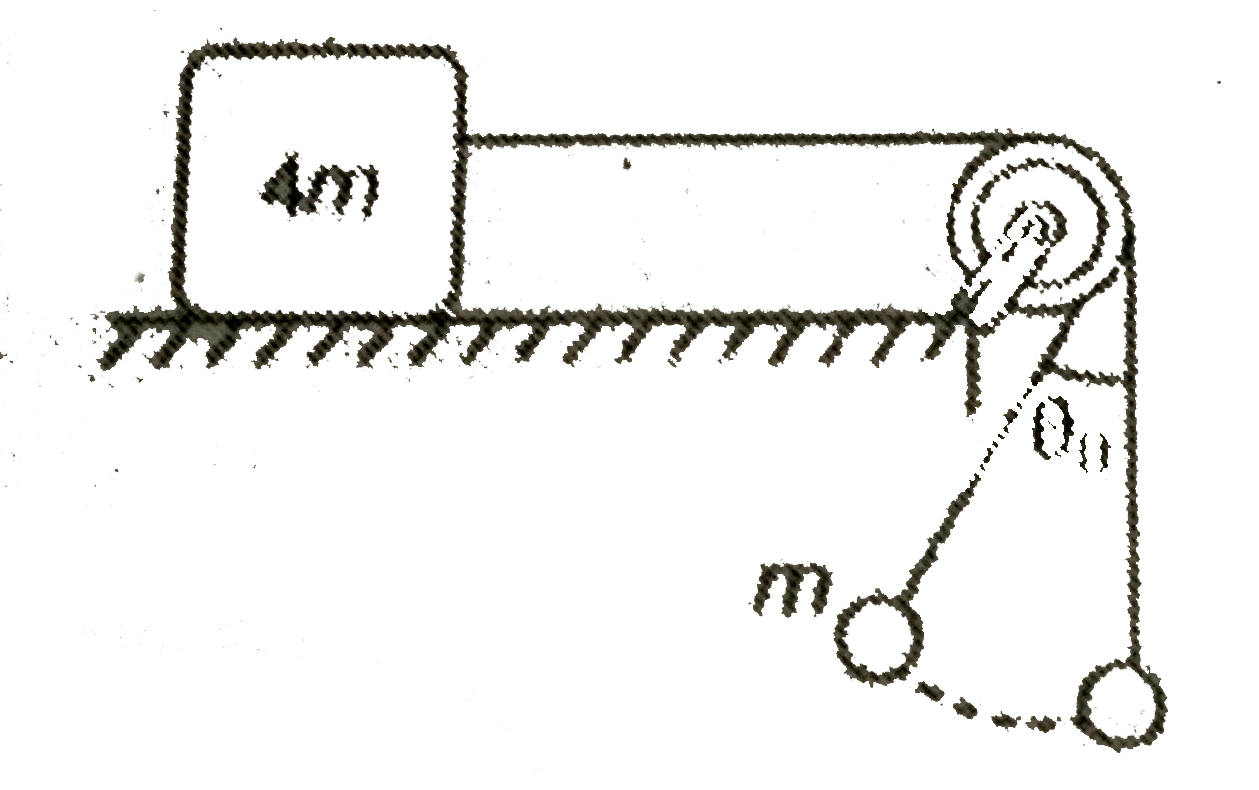
View SolutionTwo beads A and B of equal mass `m` are connected by a light inextensibe chord. They are constrined to move on a frictionless ring in vertical plane. The blocks are released from rest as shown in figure. The tension in the chord just after the release is
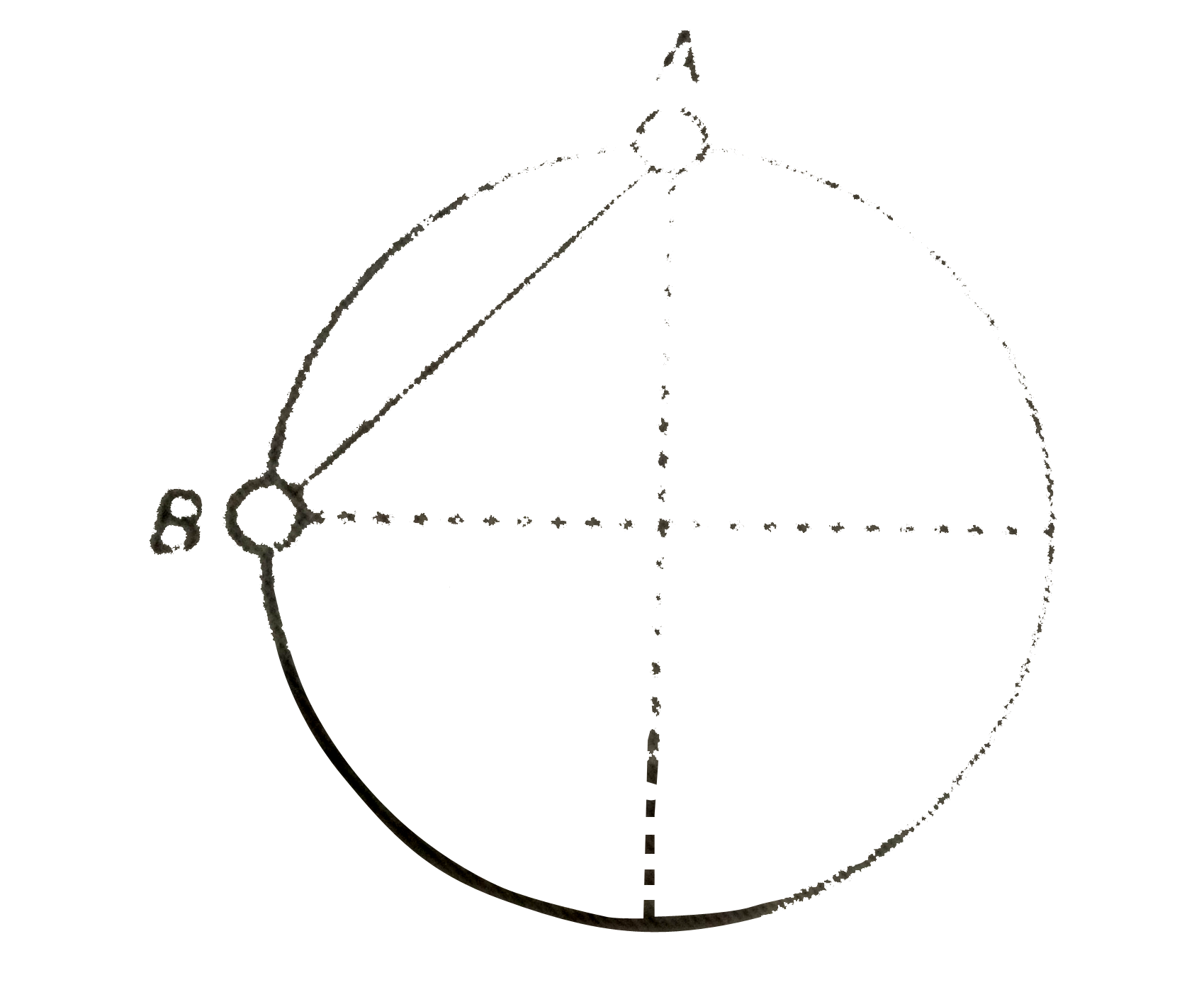
View SolutionA small block of mass `m` is released from rest from point `A` inside a smooth hemisphere bowl of radius `R`, which is fixed on group such that `OA` is horizontal. The ratio `(x)` of magnitude of centripetal force and normal reaction on the block at any point `B` varies with `theta` as :

View SolutionAn automobile enters a turn whose radius is R. The road is banked at angle `theta`. Fricton is negligible between wheels of the automobile and road, Mass of automobile is `m` and speed is `v`. Select the correct alternative.
View SolutionA ball of mass 1 kg is released from position A inside a wedge with a hemispherical cut of radius 0.5 m as shown in figure. The force exerted by the vertical wall OM on wedge, when the ball is in position B is (neglect friction everywhere) (Take `g = 10 m//s^(2)`)

View SolutionA partical of mass `m` oscillates along the horizontal diameter `AB` inside a smooth spherical `AB` inside a smooth sperical shell of radius `R`. At any instate `K.E.` of the partical is `K`. Then force applied by partical on the on the shell at this instant is:

View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant `K=((sqrt(3)+1)mg)/(R )`. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
View SolutionIn the above problem, tangential acceleration of the bead just after it is released, is
View SolutionA particle is moving in a circular path. The acceleration and momentum of the particle at a certain moment are `a=(4 hat(i)+3hat(j))m//s^(2) and p=(8 hat(i)-6hat(j))"kg-m/s"`. The motion of the particle is
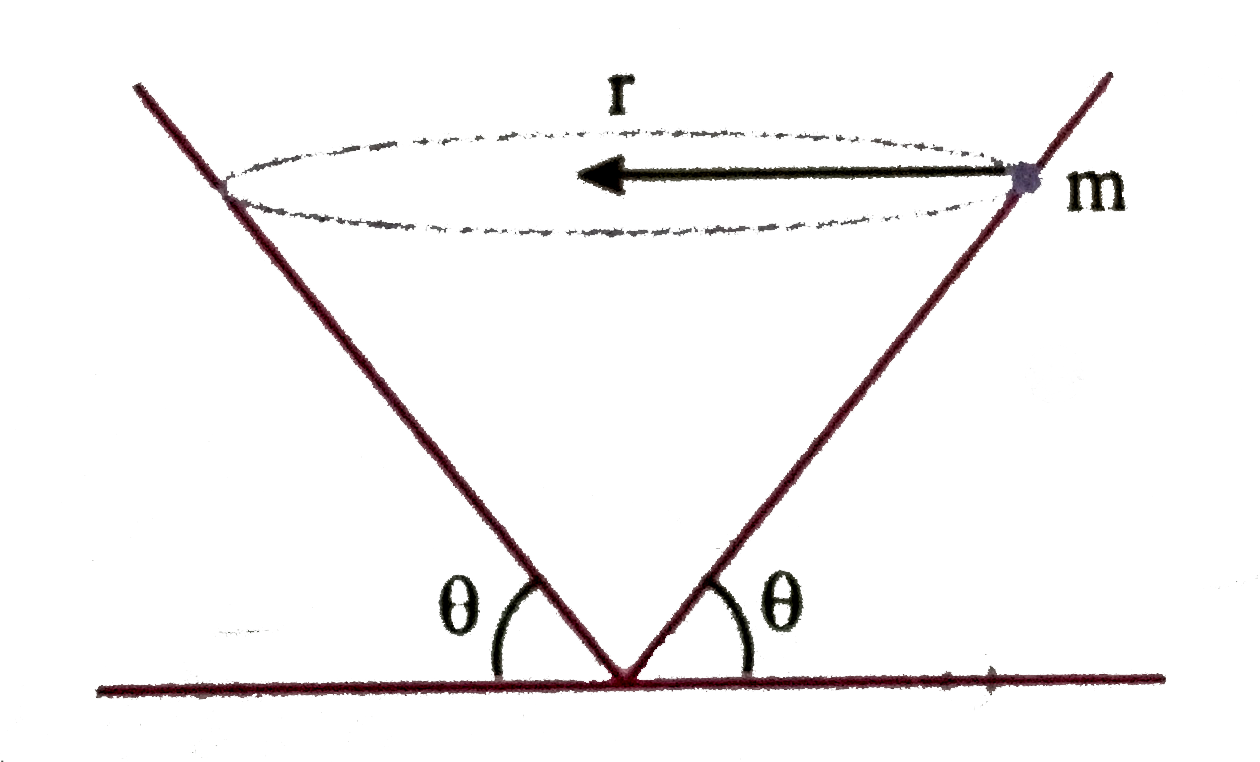
View SolutionA ball of mass `m` is rotating in a circle of radius `r` with speed `v` inside a smooth cone as shown in figure. Let `N` be the normal reaction on the ball by the cone, then choose the correct option:
View SolutionA block of mass `m=1`kg has a speed `v = 4 m//s` at `theta = 60^(@)` on a circular track of radius R = 2 m as shown in figure. Size of the block is negligible. Coefficient of friction between block and the track is `mu = 0.5`. The force of friction between the two is

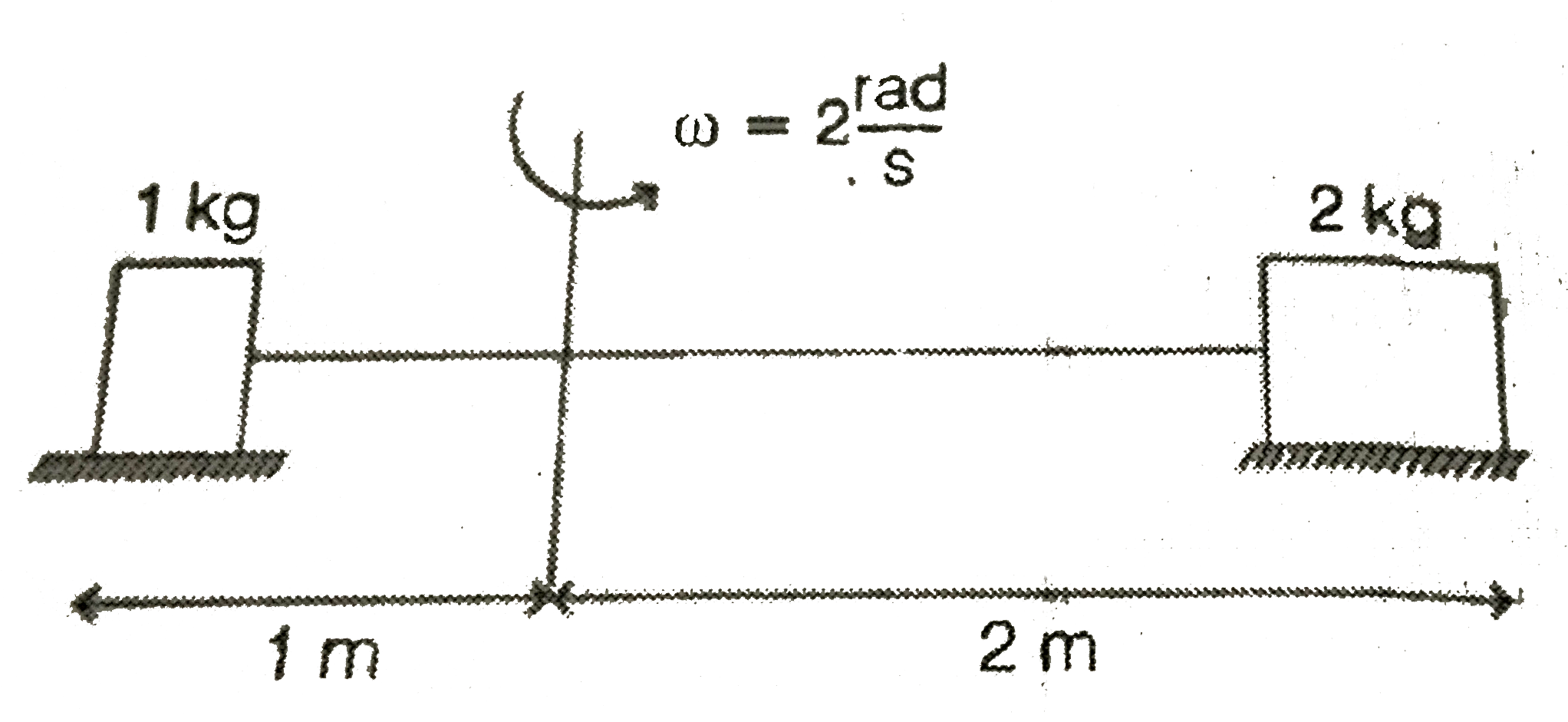
View SolutionTwo blocks of masses 1 kg and 2 kg are joined by a massless inextensible string of length 3m. Both blocks are kept on a horizontal table as shown. Friction coefficient between 2 kg block and table is zero. They are rotated about a vertical axis passing at a distance of 1m from 1 kg. Force of friction on 1kg block is (assume that there is enough friction between 1 kg block ground)
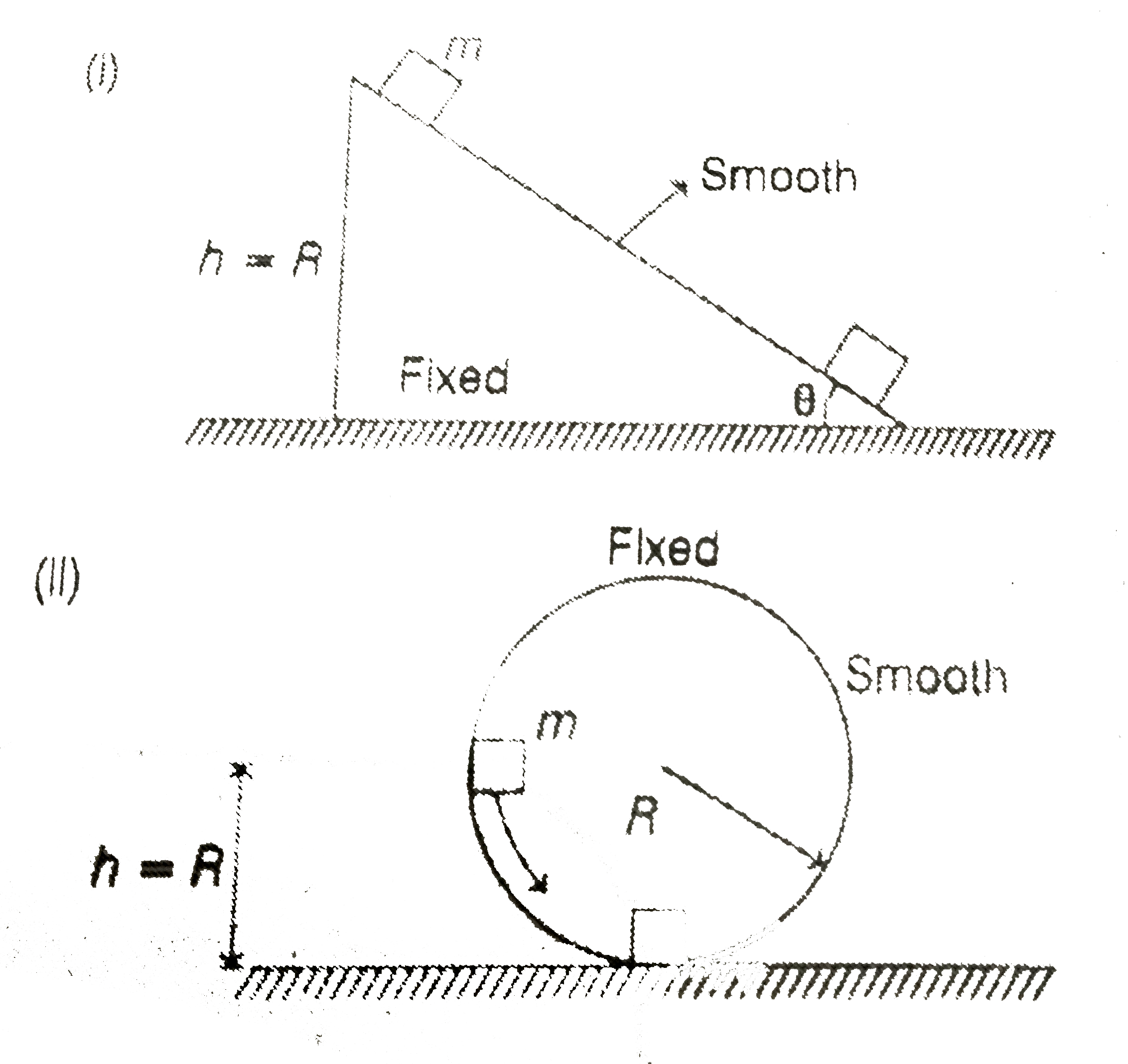
View SolutionTwo different blocks of equal mass m are released from two positions as shown in figure Net force on the block at bottommost point in case (i) is say `F_(1)` and in case (ii) is say `F_(2)`. Then
View SolutionA small collar of mass `m` is given an intial velocity of magnitude `v_(0)` on the horizontal circular track fabricated from a slender rod. If the coefficient of kinetic friction is `mu_(K)`, determine the distance travelled before the collar comes to rest. (Recognize that the friction force depends on the net normal force).

View SolutionA small ball is rolled with speed `u` from piont A along a smooth circular track as shown in figure. If `x=3R`, then

Determine the required speed u so that the ball returns to A, the point of projection after passing through C, the highest point.
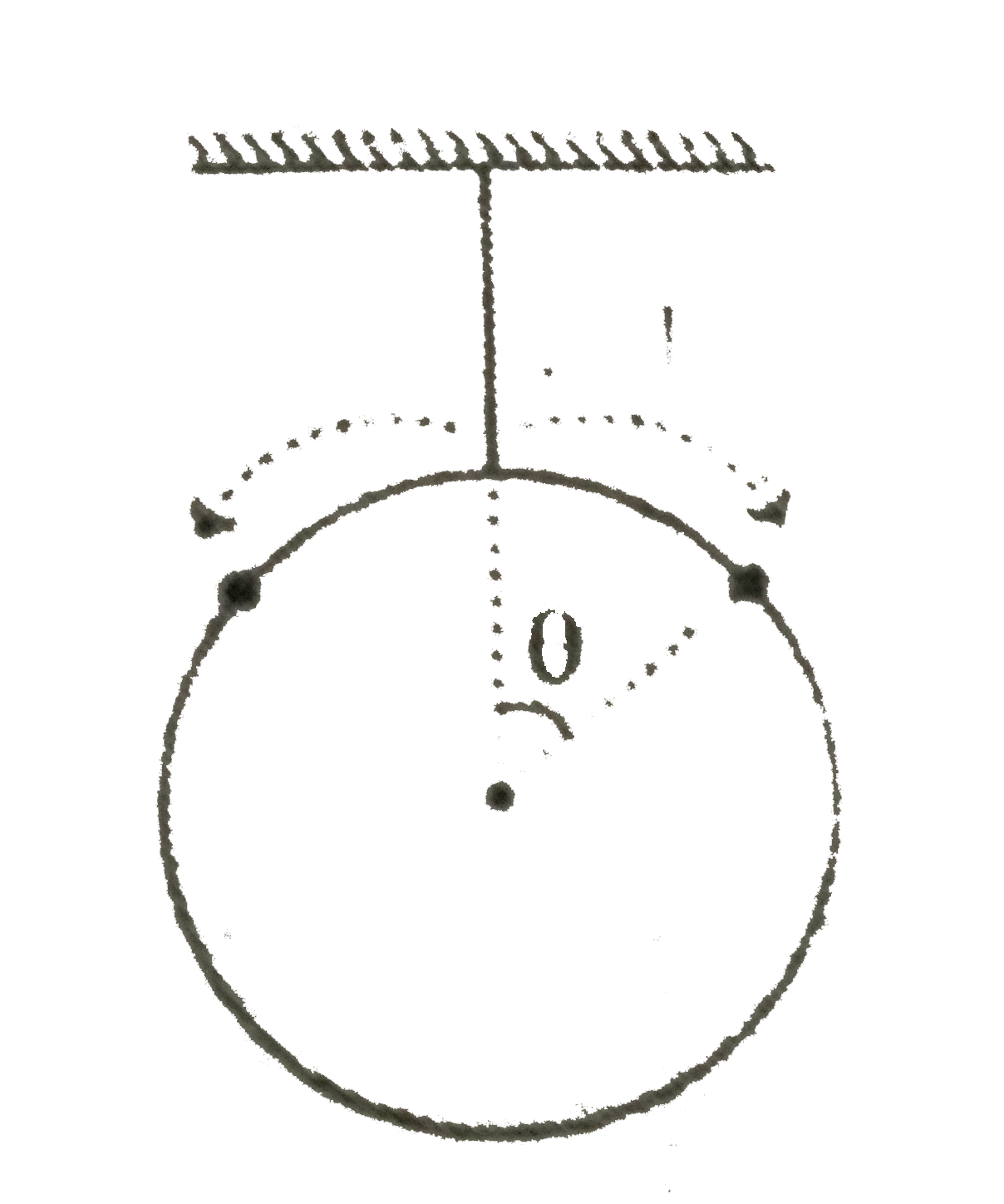
View SolutionA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass `m`, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
View SolutionA particle of mass m, moving in a circle of radius R, has a velocity `v=v_(0)(1-e^(-gamma t))` The power delivered to tha particle by the force at `t=0` is
View Solution
JEE Advanced questions and complete solutions for chapter CIRCULAR MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS CIRCULAR MOTION
- Assertion And Reason
- Check point
- Comprehension
- Example
- Exercise 10.1
- Exercise 10.2
- Exercise 10.3
- Integer
- JEE Advanced
- JEE Main
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Matrix Matching
- Medical entrances s gallery
- Miscellaneous Examples
- More than One Option is Correct
- Solved Examples
- Subjective Questions
- Taking it together