Complete Solutions to Medical entrances gallery of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| DC PANDEY NEET | Medical entrances gallery |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......
03:55View SolutionTwo particles of masses `m_(1),m_(2)` move with initial velocities `u_(1)` and `u_(2)`. On collision, one of the particles get excited to higher level, after absorbing energy. If final velocities of particles be `v_(1)` and `v_(2)` then we must have
03:07View Solution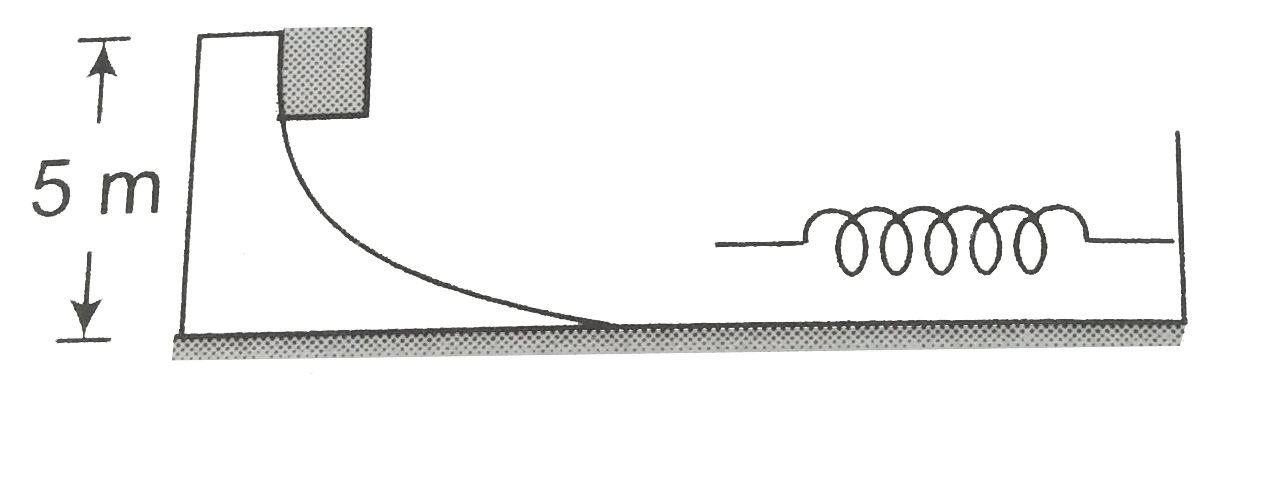
The figure shows a smooth curved track terminating in a smooth horizontal part. A spring of spring constant `400(N)//(m)` is attached at one end to a wedge fixed rigidly with the horizontal part . A 40 g mass is released from rest at a height of 5 m on the curved track. The maximum compression of the spring will be05:54View SolutionA block having mass m collides with an another stationary block having mass 2m. The lighter block comes to rest after collision. If the velocity of first block is v, then the value is coefficient of restitution will must be
02:09View SolutionA smooth curved surface of height 10 m is ended horizontally. A spring of force constant 200 `Nm^(-1)` is fixed at the horizontal end as shown in figure when an object of mass 10g is released from the top, it travels along the curved path and collides with the spring. Then, the maximum compression in the spring is (Take, `g = 10ms^(-2)`)
02:54View SolutionA frog sits on the end of a long board of length `L = 5 m`. The board rests on a frictionless horizontal table. The frog wants to jump to the opposite end of the board. What is the minimum take-off speed (in `m//s`), i.e., relative to ground `'v'` that allows the frog to do the trick? The board and the frog have equal masses.
04:02View SolutionA particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
02:04View SolutionA body from height h is dropped, if the coefficient of restitution is e, then calcualte the height achieved after one bounce.
02:03View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
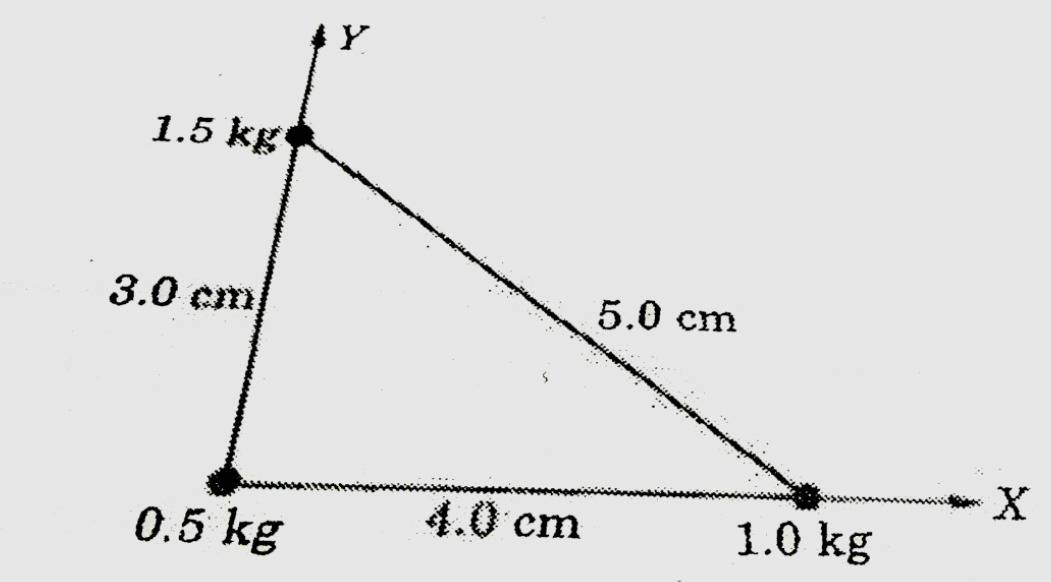 04:12View Solution
04:12View SolutionA large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
01:48View SolutionA circular disc rolls on a horizontal floor without slipping and the center of the disc moves with a uniform velocity v. Which of the following values of the velocity at a point on the rim of the disc can have?
01:35View SolutionThe linear momentum of a particle varies with time t as `p= a +bt + ct^(2)`. Then, whichh of the following is correct?
01:47View SolutionA body of mass (4m) is laying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces each mass (m) move perpedicular to each other with equal speeds (v). Total kinetic energy generated due to explosion is
02:42View SolutionThe position of center of mass of a system of particles does not depend upon the
01:54View SolutionA bullet is fired from the gun. The gun recoils, the kinetic energy of the recoil shall be-
01:38View SolutionAn explosion blows a rock into three parts. Two parts go off at right angles to each other . These two are `1 kg` first part moving with a velocity of `12 ms^(-1) and 2 kg` second part moving with a velocity of `8 ms^(-1)`. If the third part flies off with a velocity of `4 ms^(-1)`. Its mass would be
02:21View SolutionThe linear momentum is conserved in
01:12View SolutionThree particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and `hat(i), hat(j), hat(k)` are unit vectors)
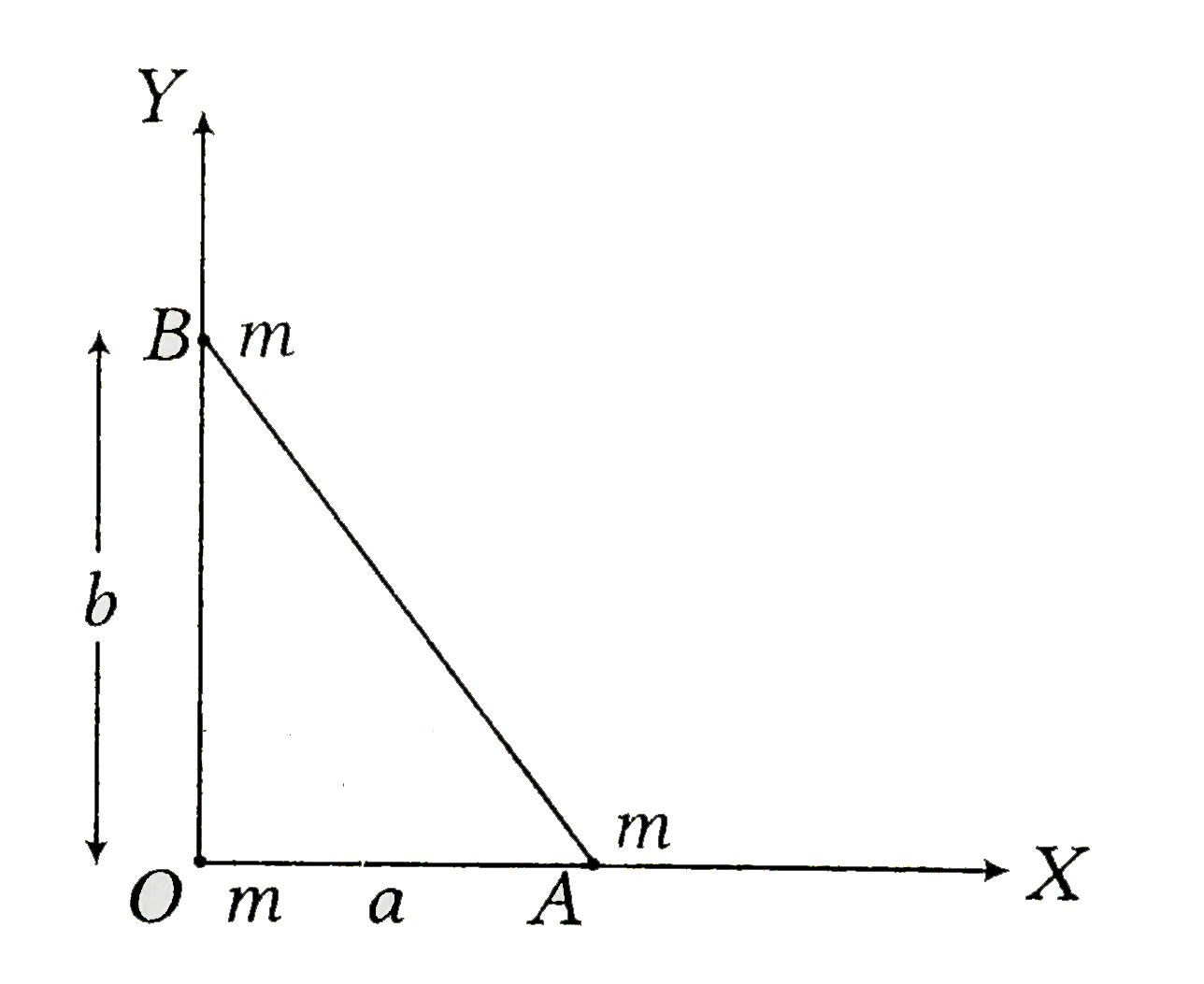 01:49View Solution
01:49View SolutionA ball of mass 'm' moving with a horizontal velocity 'v' strikes the bob of mass 'm' of a pendulum at rest. During this collision, the ball sticks with the bob of the pendulum. The height to which the combined mass raises is (g = acceleration due to gravity).
03:51View SolutionIn an inelastic collision
01:56View SolutionA body of mass `m_(1) ` moving with uniform velocity of 40 m/s collides with another mass `m_(2)` at rest and then the two together begin to moe wit h uniform velocity of 30 m/s. the ratio of their masses `(m_(1))/(m_(2))` is
01:55View SolutionTwo sphere `A and B` of masses `m_(1) and m_(2)` respectivelly colides. A is at rest initally and `B` is moving with velocity `v` along x-axis. After collision `B` has a velocity `(v)/(2)` in a direction perpendicular to the original direction. The mass `A` moves after collision in the direction.
08:19View SolutionTwo persons of masses `55 kg` and `65 kg` respectively are at the opposite ends of a boat. The length of the boat is `3.0 m` and weights `100 kg`. The `55 kg` man walks up to the `65 kg` man and sits with him. If the boat is in still water the centre of mass of the system shifts by.
01:23View SolutionA ball moving with a speed of `9m//s` strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of `30^(@)` with the original line of motion. Find the speeds of the two balls after collision.
05:41View SolutionA body of mass `0.25` kg is projected with muzzle velocity `100ms^(-1)` from a tank of mass 100 kg. What is the recoil velocity of the tank
01:48View SolutionA body of mass `m_(1) = 4kg moves at `5 hat(i) ms^(-1)` and another body of mass `m_(2) = 2kg` moves at `10hat(i)ms^(-1)`. The kinetic energy of center of mass is
01:29View SolutionA mass of 10 gm moving with a velocity of 100 cm / s strikes a pendulum bob of mass 10 gm . The two masses stick together. The maximum height reached by the system now is `(g=10m//s^(2))`
03:52View Solution
Medical entrances gallery questions and complete solutions for chapter CENTRE OF MASS of DC PANDEY PHYSICS (HINGLISH) of Class 11
