Complete Solutions to Miscellaneous Example of chapter WORK, ENERGY & POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY & POWER |
| DC PANDEY | Miscellaneous Example |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
A small mass m starts from rest and slides down the smooth spherical surface of F. Assume zero potential energy at the top. Find
(a) the change in potential energy,
(b) the kintic energy,
(c) the speed ot the mass as a function of the angle `theta` made by the radius through the mass with the vertical.
View SolutionA smooth track in the form of a quarter-circle of radius 6 m lies in the vertical plane. A ring of weight 4(N) moves from `P_(1)` and `P_(2)` under the action of forces `F_(1) , F_2` and `F_3`. is always towards `P_(2)` under the action of forces `F_(1),F_(2)` and `F_(3)` Force `F_(1)` is always towards `P_(2)` and is always (20) N in maghitude, force `F_(2)` always acts hotizontally and is always (30 N) in magnitude, force `F_(3)` always acts tangentially to the track and is of magnitude `(15-10 s) N`, where s is in metre. If the particle has speed `4 m//s` at `P_(1)`,what will its speed be at `P_(2)`?
View SolutionA single conservative force F(x) acts on a on a (1.0kg ) particle that moves along the x-axis. The potential energy U(x) is given by:
`U(x) =20 + (x-2)^(2)`
where, x is meters. At `x=5.0m` the particle has a kinetic energy of `20J`
(a) What is the mechanical energy of the system?
(b) Make a plot of U(x) as a function of x for `-10mlexle10m`, and on the same graph draw the line that represents the mechanical energy of the system. Use part (b) to determine.
(c) The least value of x and
(d) the greatest value of x between which the particle can move.
(e) The maximum kinetic energy of the particle and
(f) the value of x at which it occurs.
(g) Datermine the equation for `F(x)` as a function of x.
(h) For what (finite ) value of x does `F(x) =0`?.
View SolutionA small disc A slides down with initial velocity equal to zero from the top of a smooth hill of height H having a horizontal portion. What must be the height of the horizontal portion h to ensure the maximum distance s covered by the disc? What is it equal to?

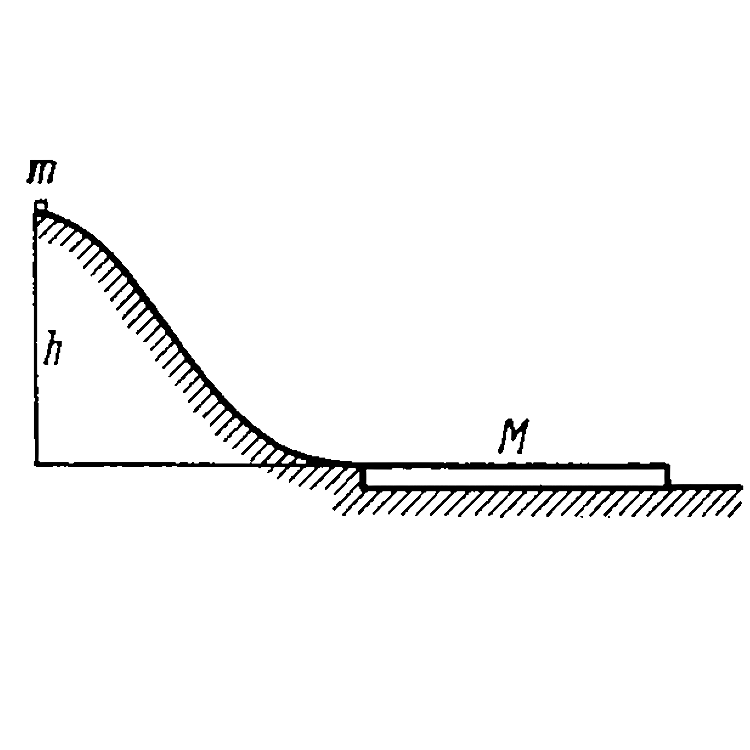
View SolutionA small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
View SolutionTwo blocks`A` and`B` are connected to each other by a string and a spring , the spring pases and a frictionlesss pulley as down over in the figure . Block `B` sides over the horizental top surface of a strionry block `C` both with the verical side of `C` , both with the same conform speed
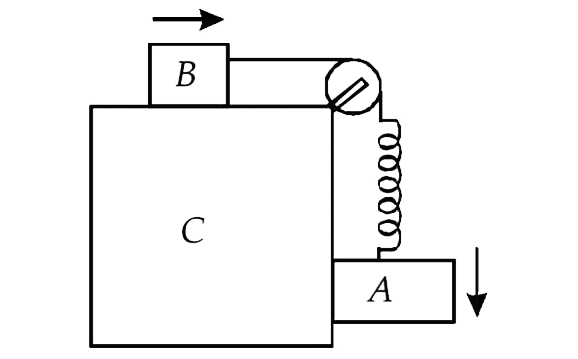
The coefficient of friction between the surface the of block is `0.2` force constant of the spring is `1960` newtons , if mass of block `A` is `2` kg , celculate the mass of block `F` and `B` and the energy stored is the spring
View Solution
Miscellaneous Example questions and complete solutions for chapter WORK, ENERGY & POWER of DC PANDEY PHYSICS (HINGLISH) of Class 11