Complete Solutions to PHYSICS of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| DISHA | PHYSICS |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
From a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
View SolutionA hollow sphere is held suspended. Sand is now poured into it in stages.The centre of mass of the sphere with the sand

View SolutionA body A of mass M while falling wertically downwards under gravity brakes into two parts, a body B of mass `(1)/(3)` M and a body C of mass `(2)/(3)` M. The center of mass of bodies B and C taken together shifts compared to that of body A towards
View SolutionFrom a uniform wire, two circular loops are made (`i`) `P` of radius `r` and (`ii`) `Q` of radius `nr`. If the moment of inertia of `Q` about an axis passing through its center and perpendicular to tis plane is `8` times that of `P` about a similar axis, the value of `n` is (diameter of the wire is very much smaller than `r` or `nr`)
View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity `v_(0).` The angular velocity `omega_(0)` acquired by the ball is
View SolutionThree bricks each of length L and mass M are arranged as shown from the wall. The distance of the centre of mass of the system from the wall is

View SolutionFour point masses, each of value `m`, are placed at the corners of square `ABCD` of side `l`. The moment of inertia of this system about an axis passing through `A` and parallel to `BD` is -
View SolutionA hoop of radius r and mass m rotating with an angular velocity `omega_0` is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
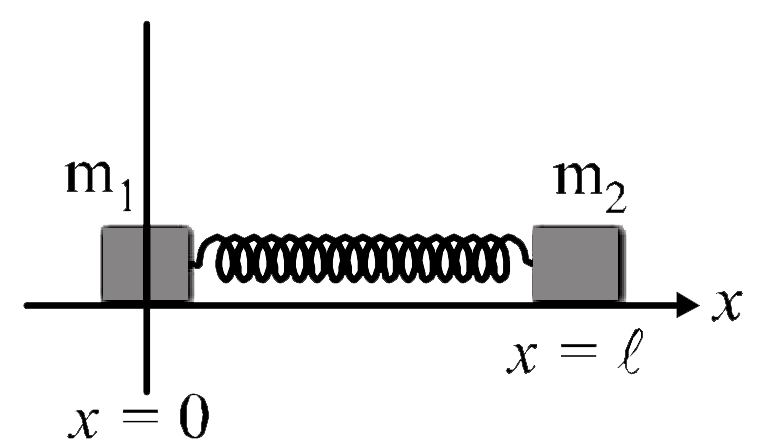
View SolutionTwo masses `m_(1)`and `m_(2)` are connected by a massless spring of spring constant k and unstretched length l. The masses are placed on a frictionless straight channel, which are consider our x-axis. They are initially at `x = 0` and ` x = l` respectively. At `t = 0,` a velocity `v_(0)` is suddenly imparted to the first particle. At a later time t, the centre of mass of the two masses is at :
View SolutionA body of mass `1.5 kg `rotating about an axis with angular velocity of` 0.3 "rad" s^( –1)` has the angular momentum of `1.8 kg m^(2)s^(–1).` The radius of gyration of the body about an axis is
View SolutionIf `vec F` is the force acting in a particle having position vector `vec r` and `vec tau` be the torque of this force about the origin, then
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is `omega`. Its cenre of mass rises to a maximum height of :
View SolutionA wheel is rolling straight on ground without slipping. If the axis of the wheel has speed v, the instantenous velocity of a point P on the rim, defined by angle `theta`, relative to the ground will be

View SolutionA solid sphere having mass m and radius r rolls down an inclined plane. Then its kinetic energy is
View SolutionA ring of mass M and radius R is rotating about its axis with angular velocity `omega.` Two identical bodies each of mass m are now gently attached at the two ends of a diameter of the ring. Because of this, the kinetic energy loss will be :
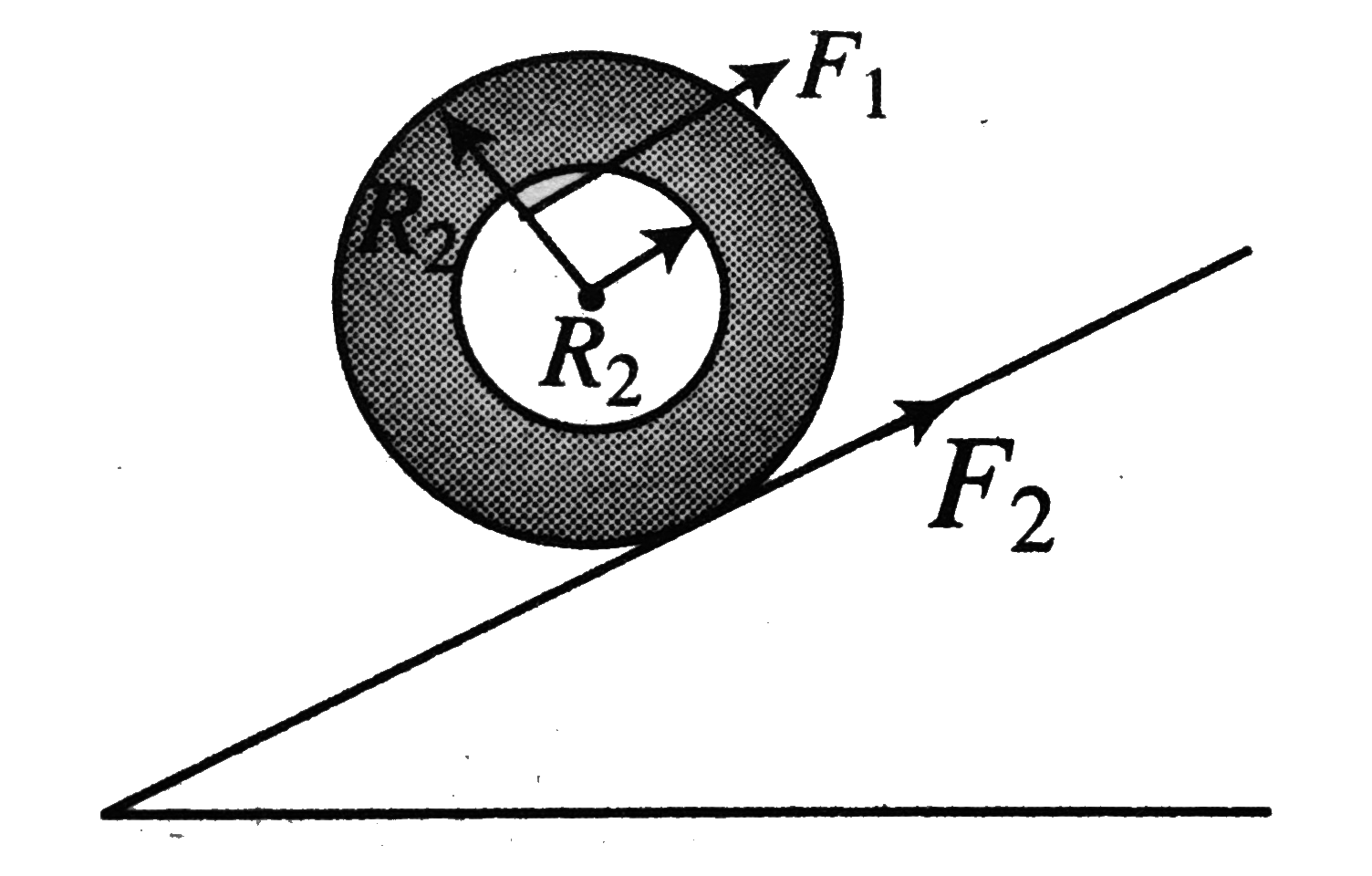
View SolutionA certain bicycle can go up a gentle incline with constant speed when the frictional force of ground pushing the rear wheel is `F_(2) = 4 N`. With what force `F_(1)` must the chain pull on the sprocket wheel if `R_(1) = 5m` and `R_(2) = 30m`?
View SolutionA wooden cube is placed on a rough horizontal table, a force is applied to the cube. Gradually the force is increased. Whether the cube slides before toppling or topples before sliding is independent of :
View SolutionFrom a circular ring of mass M and radius R, an arc corresponding to a `90^(@)` sector is removed. The moment of inertia of the ramaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is k times `MR^(2).` Then the value of k is
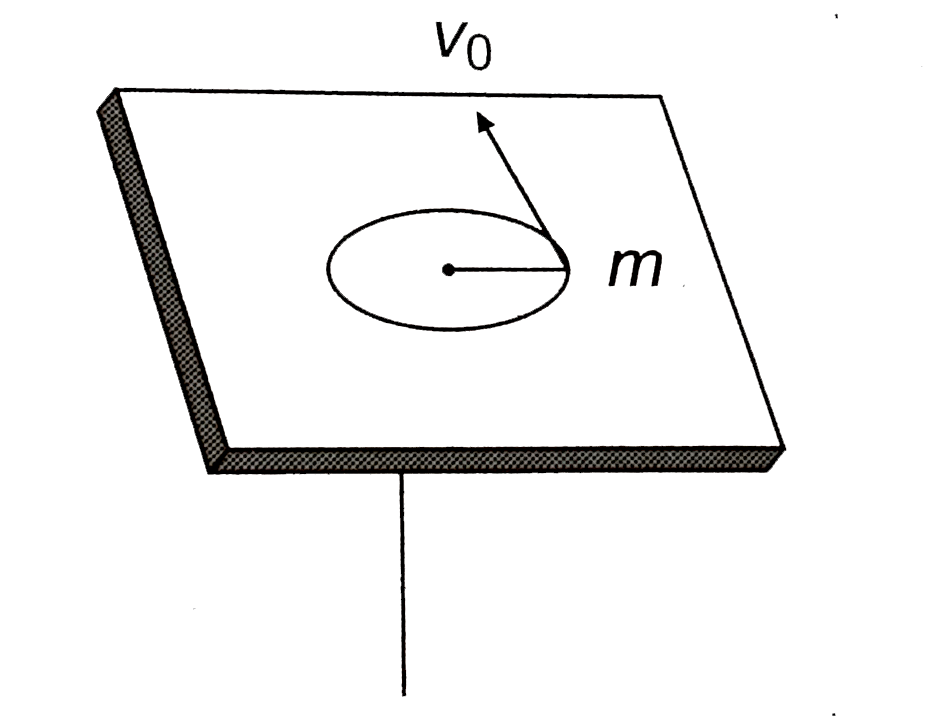
View SolutionA mass `m` moves in a circles on a smooth horizontal plane with velocity `v_(0)` at a radius `R_(0)`. The mass is atteched to string which passes through a smooth hole in the plane as shown.
The tension in string is increased gradually and finally `m` moves in a cricle of radius `(R_(0))/(2)`. the final value of the kinetic energy is
View SolutionA rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and r be its density, its rotational kinetic energy is
View SolutionA solid sphere rolls on a smooth horizontal surface at `10 m//s` and then rolls up a smooth inclined plane of inclination `30^@` with horizontal. The mass of the sphere is `2 kg`. Find the height attained by the sphere before it stops (in `m`).
View SolutionA hollow smooth uniform `A` of mass 'm' rolls without sliding on a smooth horizontal surface collides head to elastically with another stationary smooth solid sphere `B` of the same mass `m` and same radius. The ratio of kinetic energy of 'B' to that of 'A' just after the collision is -
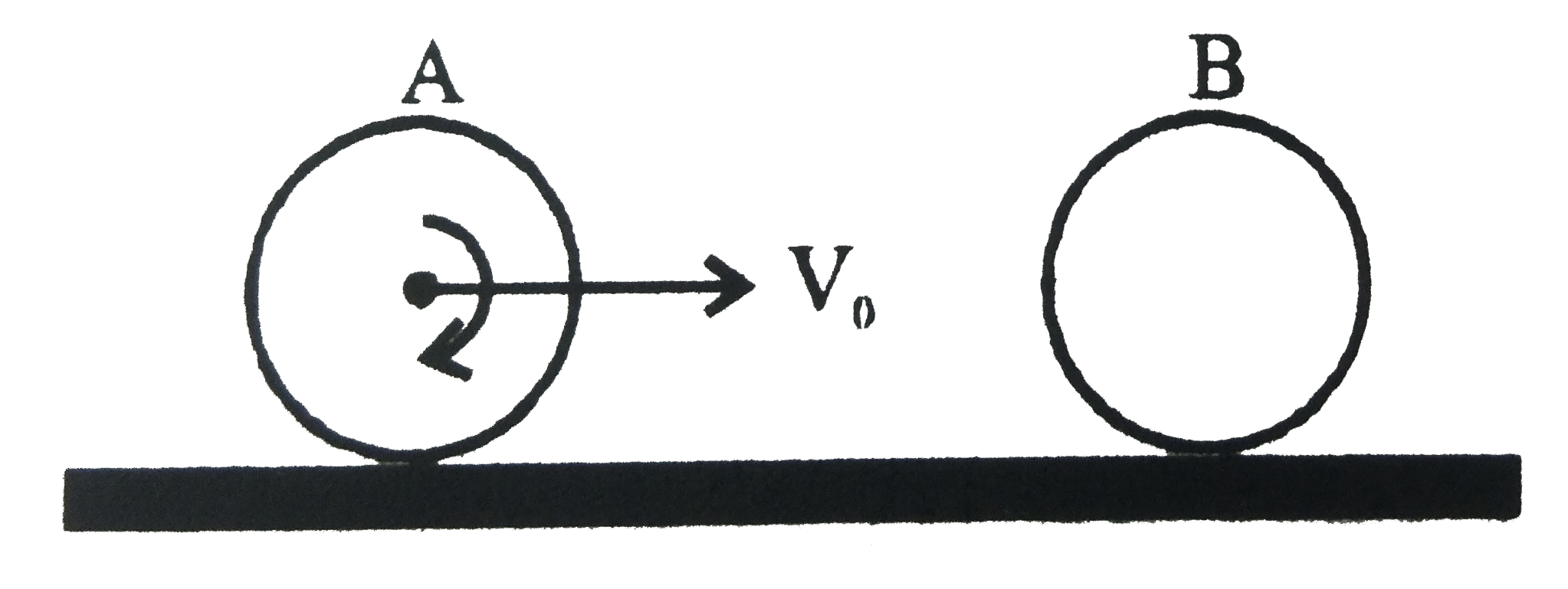 .
.
View SolutionTwo discs of same thickness but of different radii are made of two different materials such that their masses are same. The densities of the materials are in the ratio of `1 : 3.` The moments of inertia of these discs about the respective axes passing through their centres and perpendicular to their planes will be in the ratio of
View SolutionA pulley fixed to the ceiling carries a string with blocks of mass `m` and `3m` attached to its ends. The masses of string and pulley are negligible .When the system is released, its center of mass moves with what acceleration
View SolutionA ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed `v_(0).` The kinetic energy of the system is
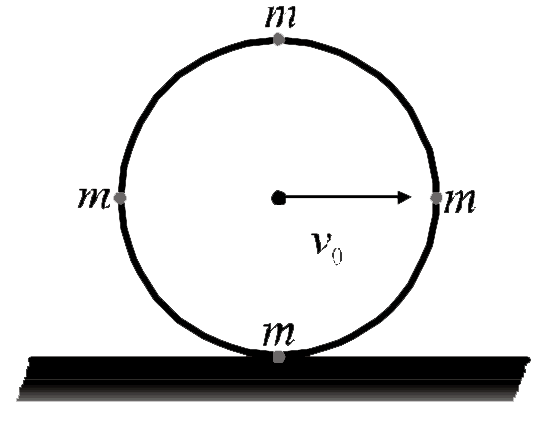
View SolutionConsider a uniform square plate of of side and mass `m`. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
View SolutionA dancer is standing on a stool rotating about the vertical axis passing through its centre. She pulls her arms towards the body reducing her moment of inertia by a factor of n. The new angular speed of turn table is proportional to
View SolutionA unifrom square plate has a small piece `Q` of an irregular shape removed and glued to the centre of the plate leaving a hole behind [Fig.] The moment of inertia about the z-axis is than
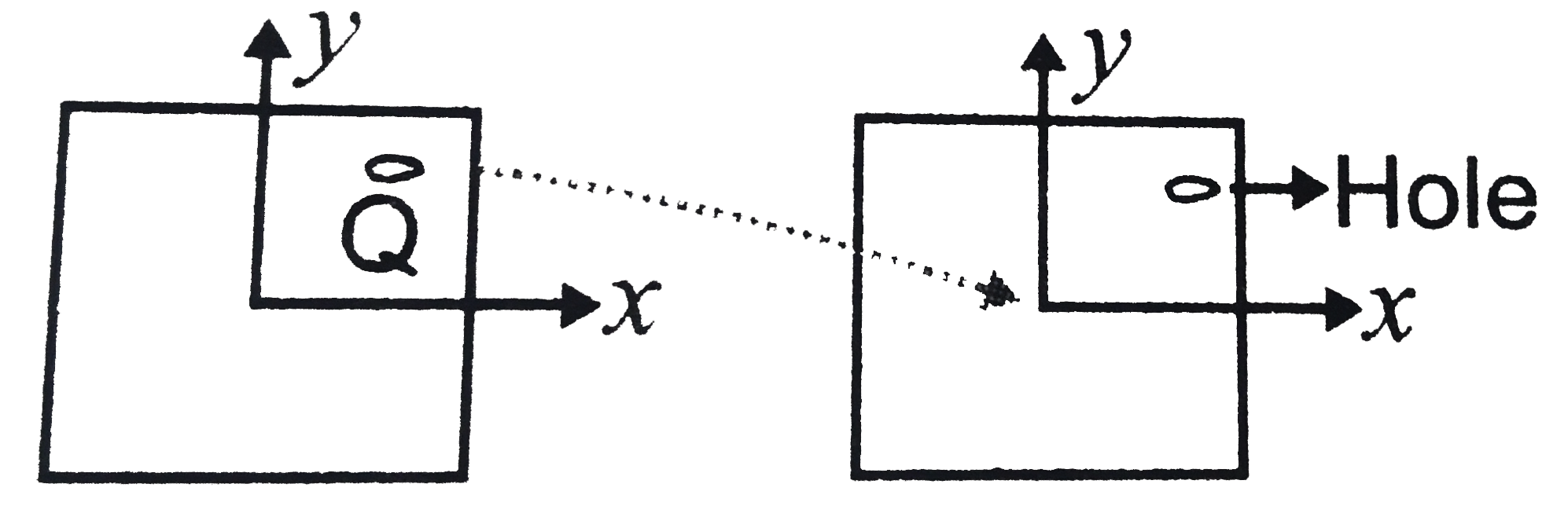
View SolutionA circular turn table has a block of ice placed at its centre. The system rotates with an angular speed w about an axis passing through the centre of the table. If the ice melts on its own without any evaporation, the speed of rotation of the system
View SolutionSeven identical disc are arranged in a hexagonal, planar pattern so as to touch each neighbour, as shown in the figure. Each disc has mass `m` and radius `r`. What is the moment of inertia of the system of seven disks about an axis passing through the centre of central disk and normal to plane of all disks ?
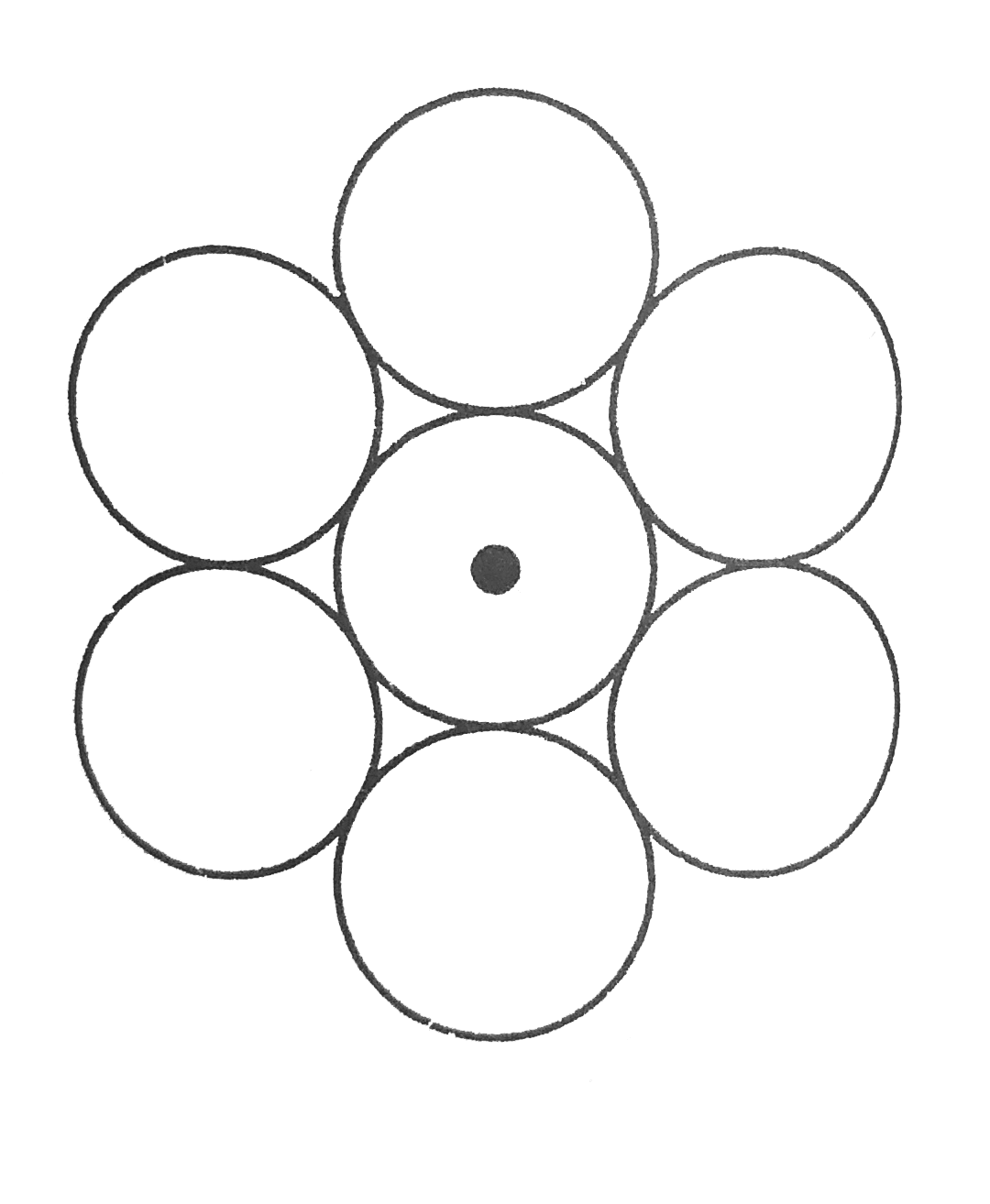 .
.
View SolutionConsidering a system having two masses `m_(1)` and `m_(2)` in which first mass is pushed towards centre of mass by a distance d, the distance required to be moved for second mass to keep centre of mass at same position is :-

View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected `(1)/(4)`th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
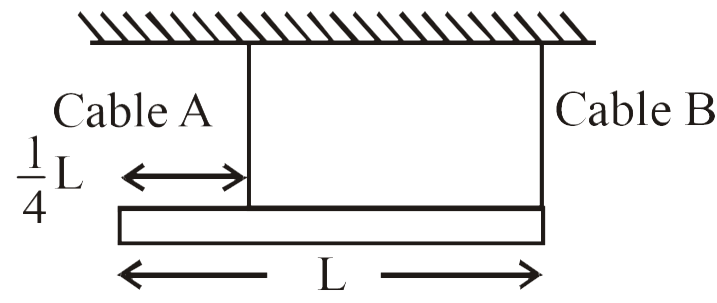
View SolutionA couple produces.
View SolutionPoint masses `1, 2, 3 "and" 4 "kg` are lying at the point `(0, 0, 0), (2, 0, 0), (0, 3, 0)` and `(–2, –2, 0)` respectively. The moment of inertia of this system about x-axis will be
View SolutionA solid sphere of mass `M` and radius `R` is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.

View SolutionThe moment of inertia of a body about a given axis is `1.2 kg m^(2)`. Initially, the body is at rest. In order to produce a rotational `KE` of `1500 J`, for how much duration, an acceleration of `25 rad s^(-2)` must be applied about that axis ?
View SolutionA gymnast takes turns with her arms and legs stretched. When she pulls her arms and legs in
View SolutionA equilaterial triangle `ABC` formed from a uniform wire has two small identical beads initially located at `A`. The triangle is set rotating about the vertical axis `AO`. Then the beads are released from rest simultaneously and allowed to slide down. one long. `AB` and the other along `AC` as shown. Neglecting frictional effects, the quantities that are conserved as the beads slide down, are.
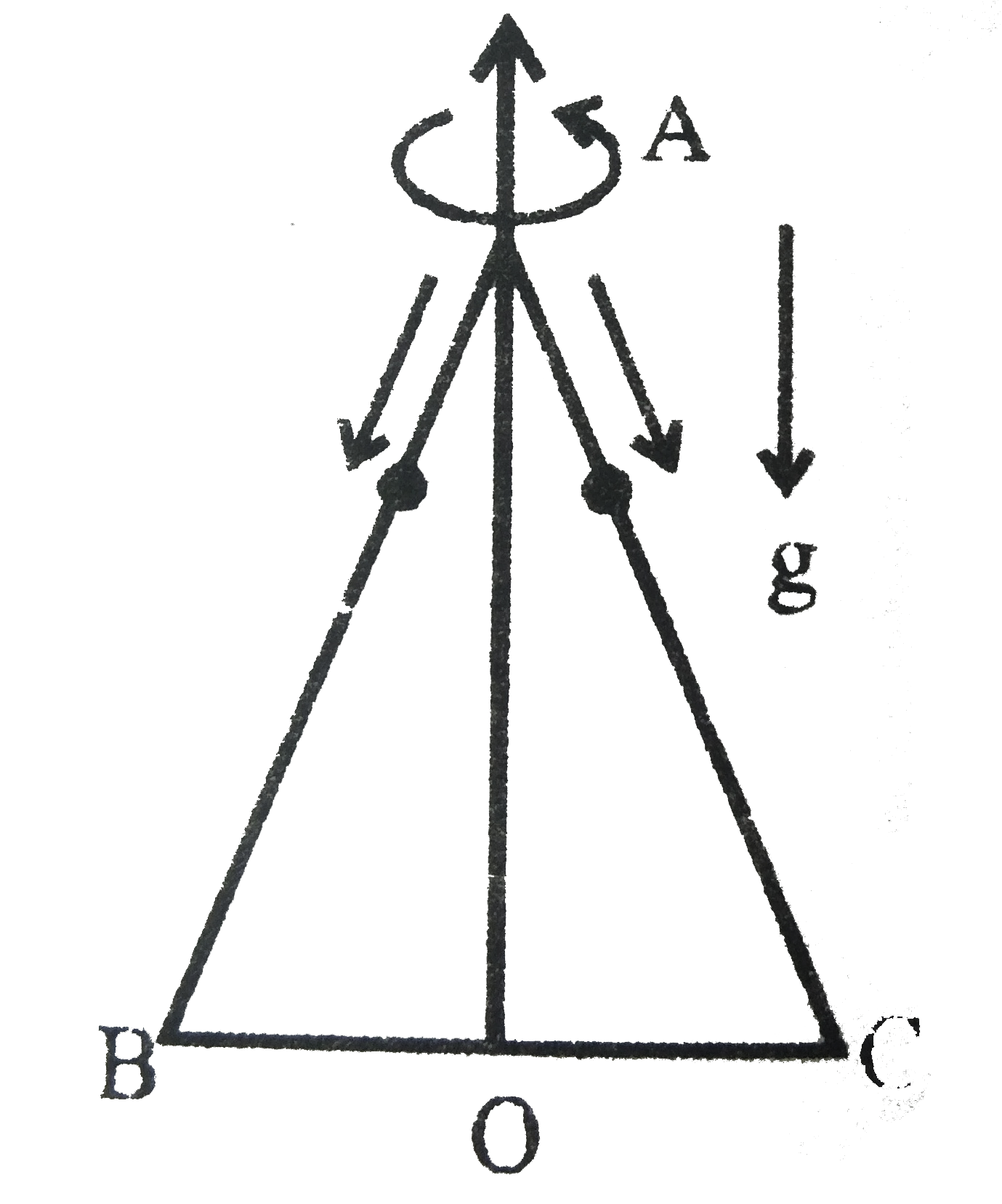 .
.
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is `mr^(2)(-(k)/(pi^(2)))`. Find the value of k.
View SolutionInitial angular velocity of a circular disc of mass `M` is `omega_(1)`. Then two small spheres of mass `m` are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
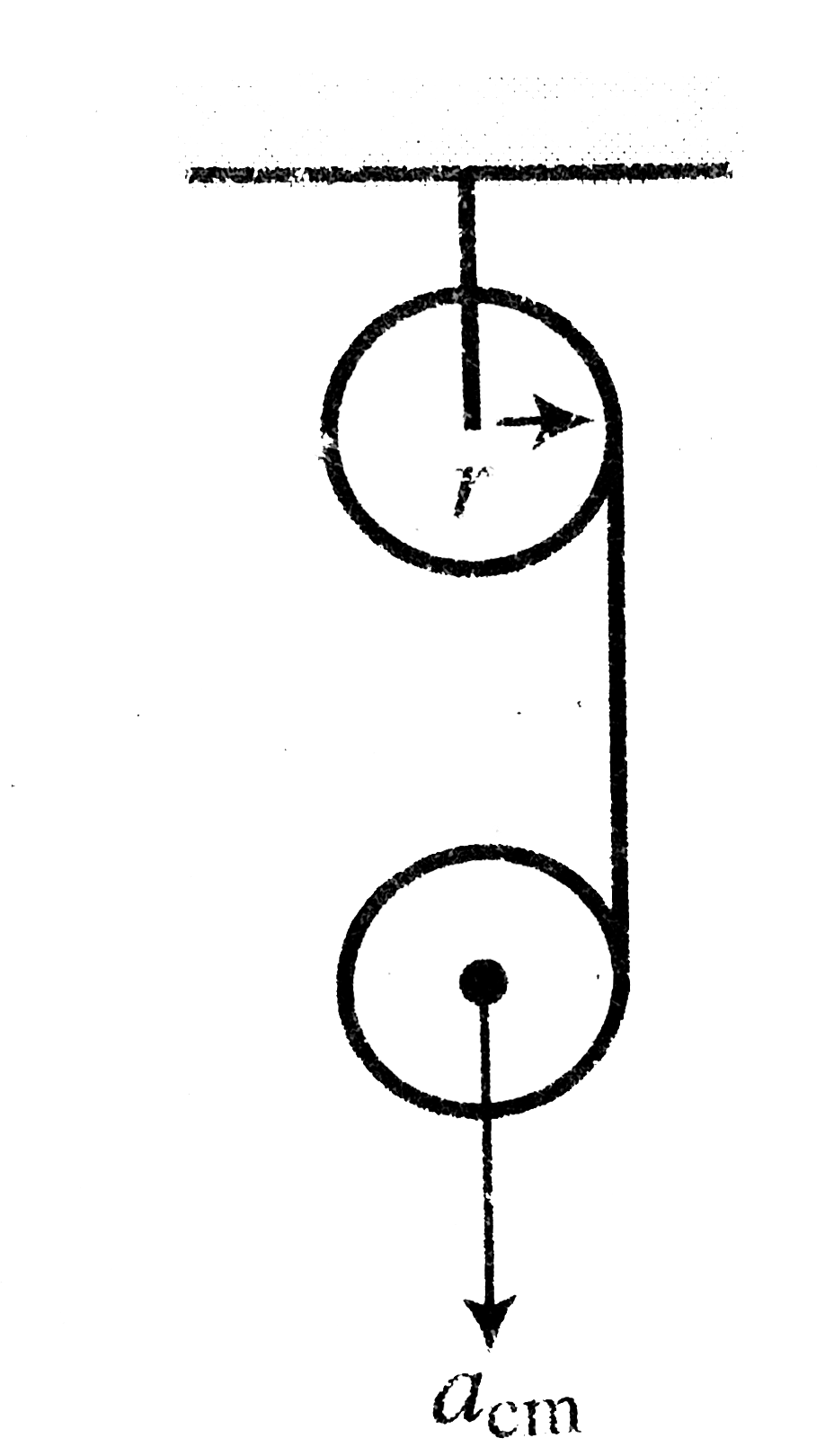
View SolutionTwo identical uniform discs of mass `m` and radius `r` are arranged as shown in the figure. If `alpha` is the angular acceleration of the lower disc and `a_(cm)` is acceleration of centre of mass of the lower disc, then relation among `a_(cm), alpha` and `r` is
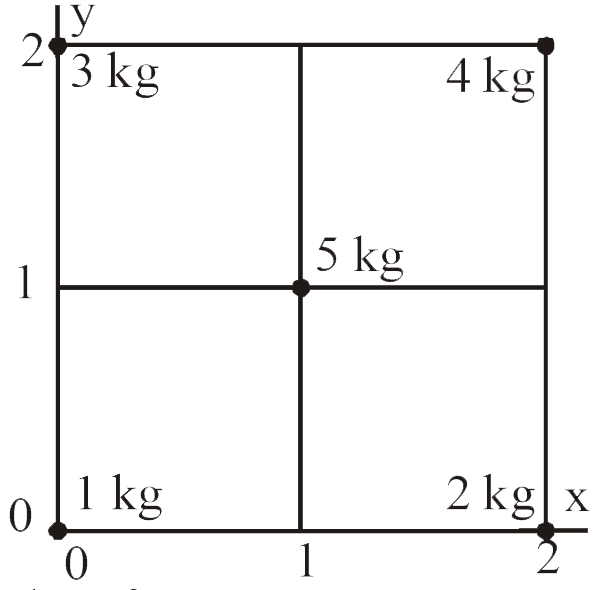
View SolutionFive masses are placed in a plane as shown in figure. The coordinates of the centre of mass are nearest to
View SolutionThree particles, each of mass `m` grams situated at the vertices of an equilateral triangle `AbC` of side `I` cm (as shown in the figure). The moment of inertia of the system about a line `AX` perpendicular to `AB` and in the plane of `ABC`, in gram-cm^2 units will be.
 .
.
View SolutionWhen a ceiling fan is switched on, it makes 10 rotations in the first 3 seconds. Assuming a uniform angular acceleration, how many rotation it will make in the next 3 seconds?
View SolutionA solid sphere spinning about a horizontal axis with an angular velocity `omega` is placed on a horizontal surface. Subsequently it rolls without slipping with an angular velocity of :
View Solution
PHYSICS questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of DISHA PHYSICS (HINGLISH) of Class 11