Complete Solutions to IN-TEXT SOLVED EXAMPLES of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| FULL MARKS | IN-TEXT SOLVED EXAMPLES |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
Two vectors `vecAandvecB` of magnitude 5 units and 7 units make an angle `60^(@)` with each other. Find the magnitude of the difference vector `vecA-vecB` and its direction with respect to the vector `vecA`.
View SolutionTwo vectors `vecAandvecB` of magnitude 5 units and 7 units make an angle `60^(@)` with each other. Find the magnitude of the difference vector `vecA-vecB` and its direction with respect to the vector `vecA`.
View SolutionWhat are the unit vectors along the negative x-direction, negative y-direction, and negative z-direction?
View SolutionTwo vectors `vecA` and `vecB` are given in the component form as `vecA=5hati+7hatj-4hatkandvecB=6hati+3hatj+2hatk`. Find `vecA+vecB,vecB+vecA,vecA-vecB,vecB-vecA`.
View SolutionGiven the vector `vecA=2hati+3hatj` what is `3vecA`?
View SolutionA vector `vecA` is given as in the following figure. Find `4vecAand-4vecA`

View SolutionGiven two vectors `vecA=2hati+4hatj+5hatkandvecB=hati+3hatj+6veck`. Find the product `vecA.vecB` and the magnitudes of `vecAandvecB`. What is the angle between them?
View SolutionCheck whether the following vectors are orthogonal.
(i) `vecA=2hati+3hatjandvecB=4hati-5hatj` (ii) `vecC=5hati+2hatjandvecD=2hati+5hatj`
View SolutionTwo vectors are given as `vecr=2hati+3hatj+5hatkandvecF=3hati-2hatj+4hatk`. Find the resultant vector `vectau=vecrxxvecF`.
View SolutionCompare the components for the following vector equations
(a) `vecF=mveca` Here m is a positive number (b) `vecp=0`
View SolutionDetermine the value of the T from the given vector equation.
`5hatj-Thatj=6hatj+3Thatj`
View SolutionCompare the components of vector equation `vecF_(1)+vecF_(2)+vecF_(3)=vecF_(4)`.
View SolutionDetermine the position vectors for the following particles which are located at points P.Q.R.S.

View SolutionA person initially at rest starts to walk 2 m towards north, then 4 m towards east, then 5 m towards south and then 3 m towards west. What is the position vector of the person at the end of the trip?
View SolutionAssume your school is located 2 km away from your home. In the morning you are going to school and in the evening you come back home. In this entire trip what is the distance travelled and the displacement covered?
View SolutionAn athlete covers 3 rounds on a circular track of radius 50 m. Calculate the total distance and displacement travelled by him.
View SolutionCalculate the displacement vector for a particle moving from a point P to Q as shown below. Calculate the magnitude of displacement.

View SolutionConsider the function `y=x^(2)`. Calculate the derivative `(dy)/(dx)` using the concept of limit, at the point x=2.
View SolutionFind the derivative with respect to t, of the function `x=A_(0)+A_(1)t+A_(2)t^(2)` where `A_(0),A_(1)andA_(2)` are constants.
View SolutionFill in the blanks.

View SolutionA particle moves along the x-axis in such a way that its coordinates x varies with time 't' according to the equation `x=2-5t+6t^(2)`. What is the initial velocity of the particle?
View SolutionSuppose two cars A and B are moving with uniform velocities with respect to ground along parallel tracks and in the same direction. Let the velocities of A and B be `35kmh^(-1)` due east and `40kmh^(-1)` due east respectively. What is the relative velocity of car B with respect to A?
View SolutionSuppose two trains A and B are moving with uniform velocities along parallel tracks but in opposite directions. Let the velocity of train A be `40kmh^(-1)` due east and that of train B be `40kmh^(-1)` due west. Calculate the relative velocities of the trains.
View SolutionConsider two trains A and B moving along parallel tracks with the same velocity in the same direction. Let the velocity of each train be `50kmh^(-1)` due east. Calculate the relative velocities of the trains.
View SolutionHow long will a boy willing near the window of a train travelling at `36kmh^(-1)` sec a train passing by in the opposite direction with a speed of `18kmh^(-1)`. The length of slow-moving train is 90m.
View SolutionA swimmer's speed in the direction of flow of a river is `12kmh^(-1)`. Against the direction
of flow of the river the swimmer's speed is `6kmh^(-1)`. Calculate the swimmer's speed in still water and the velocity of the river flow.
View SolutionA velocity time graph is given for a particle moving in x direction, as below

(a) Describe the motion qualitatively in the interval 0 to 55s.
(b) Find the distance and displacement travelled from 0 to 40 s.
Find the acceleration at t = 5s and at 20 s.
View SolutionIf the position vector of the particle is given by `vecr=3hatt^(2)hati+5thatj+4hatk`, Find the
(a) The velocity of the particle at t=3s
(b) Speed of the particle at t= 3s
(c) Acceleration of the particle at time t=3s
View SolutionAn object is thrown vertically downward. What is the acceleration experienced by the object?
View SolutionAn iron ball and a feather are both falling from a height of 10 m.
(a) What are the time taken by the iron ball and feather to reach the ground? (b) What are the velocities of iron ball and feather when they reach the ground? (Ignore air resistance and take `g=10ms^(-2)`
View SolutionIs it possible to measure the depth of a well using kinematic equations?
View SolutionA train was moving at the rate of `54kmh^(-1)` when brakes were applied. It came to rest within a distance of 225 m. Calculate the retardation produced in the train.
View SolutionSuppose an object is thrown with initial speed of 10 `ms^(-1)` at an angle `pi//4` with the horizontal, what is the range-covered? Suppose the same object is thrown similarly in the moon, will there be any change in the range? If yes, what is the change? (The acceleration due to gravity in the moon `g_("moon")=1//6 g`)
View SolutionIn the cricket game, a batsman strikes the ball such that it moves with the speed `30ms^(-1)` at an angle `30^(@)` with the horizontal as shown in the figure. The boundary line of the cricket ground is located at a distance of 75 m from the batsman? Will the ball go for a six? (Neglect the air resistance and take acceleration due to gravity `g=10ms^(-2)`.
View SolutionFind the value of x in the given figure.
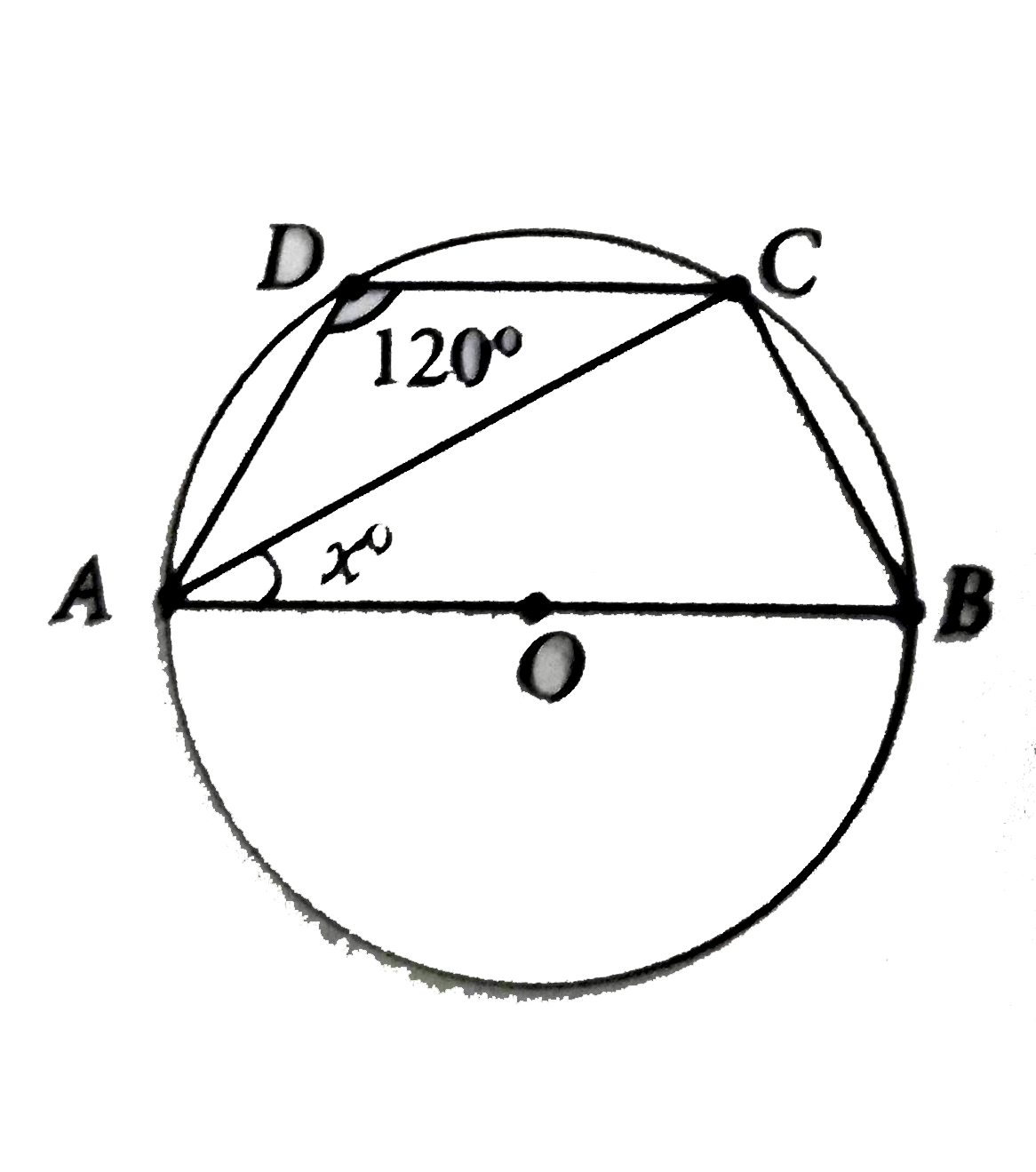
View SolutionA particle moves in a circle of radius 10 m. Its linear speed is given by v= 31 where is in second and v is in `ms^(-1)`.
(a) Find the centripetal and tangential acceleration at 1 = 2 s.
(b) Calculate the angle between the resultant acceleration and the radius vector.
View SolutionA particle is in circular motion with an acceleration `alpha=0.2rads^(-2)`.
(a) What is the angular displacement made by the particle after 5 s?
(b) What is the angular velocity at 15 s?. Assume the initial angular velocity is zero.
View SolutionThe position vector for a particle is represented be `vecr=3t^(2)hati+5thatj+6hatk`, find the velocity and speed of the particle at t=3 sec.
View SolutionA gun is fired from a place which is at distance 1.2 km from a hill. The echo of the sound s heard back at the same place of firing after 8 second. Find the speed of sound.
View SolutionA train 100 m long is moving with a speed of `60kmh^(-1)`. In how many seconds will it cross a bridge of 1 km long?
View SolutionDraw the resultant direction of the two unit vectors `hatiandhatj` Use a 2-dimensional Cartesian ystem. Is `hati+hatj` a unit vector?
View SolutionA swimmer moves across the Cauvery river of 750 m wide. The velocity of the swimmer relative to water `(vecv_(SW))` is `1.5ms^(-1)` and directed perpendicular to the water current. The velocity of water relative to the bank `(vecv_(wb))` is `1ms^(-1)`. Calculate the
velocity of the swimmer with respect to the bank of the river `(vecv_(sb))`.
(b) time taken by the swimmer to cross the Cauvery river.
View SolutionA monkey hangs on a tree. A hunter aims a gun at the monkey and fires the bullet with velocity `v_(0)` which makes angle `theta` with horizontal direction. At the instant gun fires, monkey leaves the branch and falls straight down to escape from the bulletas shown in the figure. Will bullet hit the monkey or will the monkey escape the bullet? (ignore air resistance)

View SolutionA three storey building of height 100m is located on Earth and a similar building is also located on Moon. If two people jump from the top of these buildings on Earth and Moon simultaneously, when will they reach the ground and at what speed? (`g=10ms^(-2)`)
View SolutionThe following graphs represent position - time graphs. Arrange the graphs in ascending order of increasing speed.

View SolutionTwo vectors `vecAandvecB` of magnitude 5 units and 7 units respectively make an anlge `60^(@)` with each other as shown below. Find the magnitude of the resultant vector and its direction with respect to the vector `vecA`.

View SolutionTwo vectors `vecAandvecB` of magnitude 5 units and 7 units make an angle `60^(@)` with each other. Find the magnitude of the difference vector `vecA-vecB` and its direction with respect to the vector `vecA`.
View SolutionWhat are the unit vectors along the negative x-direction, negative y-direction, and negative z-direction?
View SolutionTwo vectors `vecA` and `vecB` are given in the component form as `vecA=5hati+7hatj-4hatkandvecB=6hati+3hatj+2hatk`. Find `vecA+vecB,vecB+vecA,vecA-vecB,vecB-vecA`.
View SolutionGiven the vector `vecA=2hati+3hatj` what is `3vecA`?
View SolutionA vector `vecA` is given as in the following figure. Find `4vecAand-4vecA`

View SolutionGiven two vectors `vecA=2hati+4hatj+5hatkandvecB=hati+3hatj+6veck`. Find the product `vecA.vecB` and the magnitudes of `vecAandvecB`. What is the angle between them?
View SolutionCheck whether the following vectors are orthogonal.
(i) `vecA=2hati+3hatjandvecB=4hati-5hatj` (ii) `vecC=5hati+2hatjandvecD=2hati+5hatj`
View SolutionTwo vectors are given as `vecr=2hati+3hatj+5hatkandvecF=3hati-2hatj+4hatk`. Find the resultant vector `vectau=vecrxxvecF`.
View SolutionCompare the components for the following vector equations
(a) `vecF=mveca` Here m is a positive number (b) `vecp=0`
View SolutionDetermine the value of the T from the given vector equation.
`5hatj-Thatj=6hatj+3Thatj`
View SolutionCompare the components of vector equation `vecF_(1)+vecF_(2)+vecF_(3)=vecF_(4)`.
View SolutionDetermine the position vectors for the following particles which are located at points P.Q.R.S.

View SolutionA person initially at rest starts to walk 2 m towards north, then m towards east, then 5 m towards south and then 3 m towards west. What is the position vector of the person at the end of the trip?

View SolutionAssume your school is located 2 km away from your home. In the morning you are going to school and in the evening you come back home. In this entire trip what is the distance travelled and the displacement covered?

View SolutionAn athlete covers 3 rounds on a circular track of radius 50 m. Calculate the total distance and displacement travelled by him.
View SolutionCalculate the displacement vector for a particle moving from a point P to Q as shown below. Calculate the magnitude of displacement.

View SolutionConsider the function `y=x^(2)`. Calculate the derivative `(dy)/(dx)` using the concept of limit, at the point x=2.
View SolutionFind the derivative with respect to t, of the function `x=A_(0)+A_(1)t+A_(2)t^(2)` where `A_(0),A_(1)andA_(2)` are constants.
View SolutionConsider an object travelling in a semi-circular path from point to point P in 5 second, as is shown in the Figure given below. Calculate the average velocity and average speed.

View SolutionA particle moves along the x-axis in such a way that its coordinates x varies with time 't' according to the equation `x=2-5t+6t^(2)`. What is the initial velocity of the particle?
View SolutionSuppose two cars A and B are moving with uniform velocities with respect to ground along parallel tracks and in the same direction. Let the velocities of A and B be `35kmh^(-1)` due east and `40kmh^(-1)` due east Velocity Ve respectively. What is the relative velocity of car B with respect to A?

View SolutionSuppose two trains A and B are moving with uniform velocities along parallel tracks but in opposite directions. Let the velocity of train A be `40kmh^(-1)` due east and that of train B be `40kmh^(-1)` due west. Calculate the relative velocities of the trains.
View SolutionConsider two trains A and B moving along parallel tracks with the same velocity in the same direction. Let the velocity of each train be `50kmh^(-1)` due east. Calculate the relative velocities of the trains.
View SolutionHow long will a boy willing near the window of a train travelling at `36kmh^(-1)` sec a train passing by in the opposite direction with a speed of `18kmh^(-1)`. The length of slow-moving train is 90m.
View SolutionA swimmer's speed in the direction of flow of a river is `12kmh^(-1)`. Against the direction
of flow of the river the swimmer's speed is `6kmh^(-1)`. Calculate the swimmer's speed in still water and the velocity of the river flow.
View SolutionA velocity time graph is given for a particle moving in x direction, as below

(a) Describe the motion qualitatively in the interval 0 to 55s.
(b) Find the distance and displacement travelled from 0 to 40 s.
Find the acceleration at t = 5s and at 20 s.
View SolutionIf the position vector of the particle is given by `vecr=3hatt^(2)hati+5thatj+4hatk`, Find the
(a) The velocity of the particle at t=3s
(b) Speed of the particle at t= 3s
(c) Acceleration of the particle at time t=3s
View SolutionAn object is thrown vertically downward. What is the acceleration experienced by the object?
View SolutionAn iron ball and a feather are both falling from a height of 10 m.
(a) What are the time taken by the iron ball and feather to reach the ground? (b) What are the velocities of iron ball and feather when they reach the ground? (Ignore air resistance and take `g=10ms^(-2)`
View SolutionIs it possible to measure the depth of a well using kinematic equations?
View SolutionA train was moving at the rate of `54kmh^(-1)` when brakes were applied. It came to rest within a distance of 225 m. Calculate the retardation produced in the train.
View SolutionSuppose an object is thrown with initial speed of 10 `ms^(-1)` at an angle `pi//4` with the horizontal, what is the range-covered? Suppose the same object is thrown similarly in the moon, will there be any change in the range? If yes, what is the change? (The acceleration due to gravity in the moon `g_("moon")=1//6 g`)
View SolutionIn the cricket game, a batsman strikes the ball such that it moves with the speed `30ms^(-1)` at an angle `30^(@)` with the horizontal as shown in the figure. The boundary line of the cricket ground is located at a distance of 75 m from the batsman? Will the ball go for a six? (Neglect the air resistance and take acceleration due to gravity `g=10ms^(-2)`.
View SolutionCalculate the angle `theta` subtended by the two adjacent wooden spokes of a bullock cart wheel is shown in the figure. Express the angle in both radian and degree.

View SolutionA particle moves in a circle of radius 10 m. Its linear speed is given by v= 31 where is in second and v is in `ms^(-1)`.
(a) Find the centripetal and tangential acceleration at 1 = 2 s.
(b) Calculate the angle between the resultant acceleration and the radius vector.
View SolutionA particle is in circular motion with an acceleration `alpha=0.2rads^(-2)`.
(a) What is the angular displacement made by the particle after 5 s?
(b) What is the angular velocity at 15 s?. Assume the initial angular velocity is zero.
View SolutionThe position vector for a particle is represented be `vecr=3t^(2)hati+5thatj+6hatk`, find the velocity and speed of the particle at t=3 sec.
View SolutionA gun is fired from a place which is at distance 1.2 km from a hill. The echo of the sound s heard back at the same place of firing after 8 second. Find the speed of sound.
View SolutionA train 100 m long is moving with a speed of `60kmh^(-1)`. In how many seconds will it cross a bridge of 1 km long?
View SolutionDraw the resultant direction of the two unit vectors `hatiandhatj` Use a 2-dimensional Cartesian ystem. Is `hati+hatj` a unit vector?
View SolutionA swimmer moves across the Cauvery river of 750 m wide. The velocity of the swimmer relative to water `(vecv_(SW))` is `1.5ms^(-1)` and directed perpendicular to the water current. The velocity of water relative to the bank `(vecv_(wb))` is `1ms^(-1)`. Calculate the
velocity of the swimmer with respect to the bank of the river `(vecv_(sb))`.
(b) time taken by the swimmer to cross the Cauvery river.
View SolutionA monkey hangs on a tree. A hunter aims a gun at the monkey and fires the bullet with velocity `v_(0)` which makes angle `theta` with horizontal direction. At the instant gun fires, monkey leaves the branch and falls straight down to escape from the bulletas shown in the figure. Will bullet hit the monkey or will the monkey escape the bullet? (ignore air resistance)

View SolutionA three storey building of height 100m is located on Earth and a similar building is also located on Moon. If two people jump from the top of these buildings on Earth and Moon simultaneously, when will they reach the ground and at what speed? (`g=10ms^(-2)`)
View SolutionThe following graphs represent position - time graphs. Arrange the graphs in ascending order of increasing speed.

View Solution
IN-TEXT SOLVED EXAMPLES questions and complete solutions for chapter KINEMATICS of FULL MARKS PHYSICS (TAMIL ENGLISH) of Class 11
All Exercises from FULL MARKS Class 11 PHYSICS KINEMATICS
- ADDITIONAL QUESTIONS SOLVED (I.MULTIPLE CHOICE)
- ADDITIONAL QUESTIONS SOLVED (LONG ANSWER QUESTIONS)
- ADDITIONAL QUESTIONS SOLVED (NUMERICAL QUESTIONS)
- ADDITIONAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS (1 MARK))
- ADDITIONAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS - 1 (2 MARKS))
- ADDITIONAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS - 1 (3 MARKS))
- IN-TEXT SOLVED EXAMPLES
- TEXTUAL QUESTIONS SOLVED (LONG ANSWER QUESTIONS)
- TEXTUAL QUESTIONS SOLVED (MULTIPLE CHOICE QUESTIONS:)
- TEXTUAL QUESTIONS SOLVED (NUMERICAL QUESTIONS)
- TEXTUAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS)