Complete Solutions to EXAMPLE of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| HC VERMA | EXAMPLE |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
The motor of an engine is rotating about its axis with an angular velocity of 100 rev/minute. It comes to rest in 15 s, after being switched off. Assuming constant angular deceleration, calculate the number of revolutions made by it before coming to rest.
View SolutionStarting from rest, a fan takes five seconds to attain the maximum speed of 400 rpm (revolutions per minute). Assuming constant acceleration find the time taken by the fan in attaining half the maximum speed.
View SolutionA bucket is being lowered down into a well through a rope passing over a fixed pulley of radius 10 cm. Assume that the rope does not slip on the pulley. Find the angular velocity and angular acceleration of the pulley at an instant when the bucket is going down at at speed of 20 cm/s and has an acceleration of `4.0 m/s^2`.
View SolutionConsider a pulley fixed at its centre of mass by a clamp. A light rope is wound over it and the free end is tied to block. The tension in the rope is T. a. Write the forces acting on the pulley. How are they related? B. Locate the axis of rotation. c. Find the torque of the forces abut the axis of rotation.
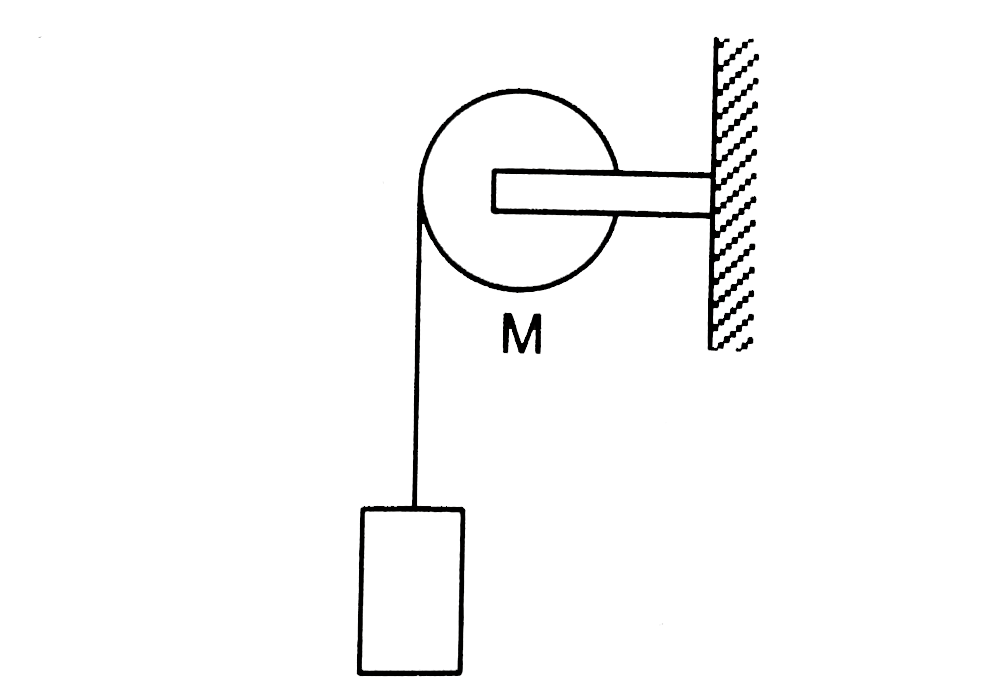
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 `rad s^-2` in the wheel. Calculate the moment of inertia of the wheel.

View SolutionA wheel is rotating at an angular speed `omega` about its axis which is kept vertical. An identical wheel initially at rest is gently dropped into the same axle and the two wheels start rotating with a common angular speed. Find this common angular speed.
View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionConsider a light rod with two heavy mass particles at its ends. Let AB be a line perpendicular to the rod as shown in figure. What is the moment of inertia of the system about AB?

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionFind the moment of inertia of a uniform ring of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA uniform sphere of mass 200 g rolls without slipping on a plane surface so that its centre moves at a speed of 2.00 cm/s. Find its kinetic energy.
View Solution
EXAMPLE questions and complete solutions for chapter ROTATIONAL MECHANICS of HC VERMA of Class 11