Complete Solutions to Objective -1 of chapter ROTATIONAL MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| HC VERMA | Objective -1 |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
Let `vecA` be a unit vector along the axis of rotation of a purely rotating body and `vecB` be a unit vector along the velocity of a particle P of the body away from the axis. The value of `vecA.vecB` is
View SolutionLet `vecA` be a unit vector along the axis of rotation of a purely rotating body and `vecB` be a unit vector along the velocity of a particle P of the body away from the axis. The value of `vecA.vecB` is
View SolutionA particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View SolutionA body is in pure rotation. The linear speed 'v' of a particle, the distance 'r' of the particle from the axis and the angular velocity `omega` of the body are related as `omega=v/r`. Thus
View SolutionFrom the figure find x and y.
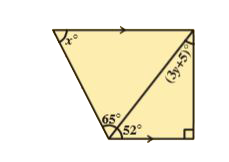
View SolutionA body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on axis is
View SolutionA body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on axis is
View SolutionIf F is the force acting on a particle having position vector `vec r` and `vec tau` be the torque of this force about the origin , then,
View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity `omega`. The force exerted by the clamp on the rod has a horizontal component
View SolutionA uniform rod is kept vertically on a horizontally smooth surface at a point O. IF it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
View SolutionA circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia `I_A and I_B` is
View SolutionEqual torques asct on the discs A and B of theh previous problem, initially both being at rest. At a later instant, theliear speeds of a point on therim of a A another potin on the rim of B are `V_A and V_B` respectively. We have
View SolutionA closed tube partly filled with water lies is a horizontal plane. If the tube is rotated about perpendicular bisector, the moment of inertia of the system. ......
View SolutionThe moment of inertia of a uniform semi-circular wire of mass 'M' and radius 'r' about a line perpendicular to the plane of the wire through the center is
View SolutionLet `I_1 and I_2` be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminum and the second of iron.
View SolutionA body having its centre of mass at the origin has three of its particles at `(a,0,0), (0,a,0),(0,0,a).` The moments of inertia of the body about the X and Y axes are 0.20 kg `-m^2` each. The moment of inertia about the Z-axis
View SolutionA cubical block of mass M and edge a slides down a rougg inclined plane of inclination `theta` with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with an angular speed `omega`. Two particles having mass `m` each are now attached at diametrically opposite points. The angular speed of the ring will become
View SolutionA man is sitting on a rotating stool with his arms outstretched. If suddenly he folds his arms the angular velocity of the man would
View SolutionThe center of a wheel rolling on a plane surface moves with a speed `v_0`. A particle on the rim of the wheel at the same level as the center will be moving at speed
View SolutionA wheel of radius 20 cm is pushed ot move it on a rough horizontal surface. It is found to move through a distance of 60 cm on the road during the time it completes one revolutionabout the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is
View SolutionThe angular velocity of the engine (and hence of the wheel) on a scooter is proportional to the petrol input per second. The scooter is moving on a frictionless road with uniform velocity. If the petrol input is increased by 10% the linear velocity of the scooter is increased by
View SolutionA solid sphere, a hollow sphere and a disc, all having the same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The least time will be taken in reaching the bottom by
View SolutionA solid sphere, a ring and a disc all having same mass and radius are placed at the top of an incline and released. The friction coefficient between the objects and the incline are same but not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
View SolutionIn the previous question the smallest kinetic energy at the bottom of the incline will be achieved by
View SolutionA string of negligible thicknes is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the sitting an pulls the cylinder towards him figure. There is no slipping anywhere. The length of the string passed through the hand of the man whicle the cylinder reaches his hands is

View Solution
Objective -1 questions and complete solutions for chapter ROTATIONAL MECHANICS of HC VERMA of Class 11