Complete Solutions to MISCELLANEOUR EXERCISE : 15 of chapter STATISTICS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | STATISTICS |
| KUMAR PRAKASHAN | MISCELLANEOUR EXERCISE : 15 |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
The mean and variance of eight observation are 9 and 9.25, respectively. If six of the observation are 6,7,10,12,12 and 13, find the remaining two observations.
View SolutionThe mean and variance of 7 observation are 8 and 16, respectively. If five of the observation are 2,4,10,12,14 . Find the remaining two observations.
View SolutionThe mean and standard deviation of six observations are 8 and 4, respectively. If each observation is multiplied by 3, find the new mean and new standard deviation of the resulting observations
View SolutionGiven that `bar(x)` is the mean and `sigma^(2)` is the variance of n observation `x_(1), x_(2), …x_(n).` Prove that the mean and `sigma^(2)` is the variance of n observations `ax_(1),ax_(2), ax_(3),….ax_(n)` are `abar(x)` and `a^(2)sigma^(2)`, respectively, `(ane0)`.
View SolutionThe mean and standard deviation of 20 observations are found to be 10 and 2, respectively. On rechecking , it was found that an observation 8 was incorrect . Calculate the correct mean and standard deviation in each of the following cases:
(i) If wrong item is omitted.
(ii) If it is replaced by 12.
View SolutionThe mean and standard deviation of marks obtained by 50 students of a class in three subjects , mathematics, physics and chemistry are given below:
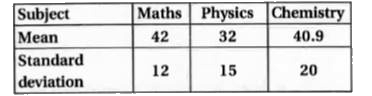
Which of the three subjects shows the highest variability in marks and which shows the lowest?
View SolutionThe mean and standard deviation of a group of 100 observations were found to be 20 and 3, respectively. Later on it was found that three observations were incorrect, which were recorded as 21, 21 and 18. Find the mean and standard deviation if the incorrect observations are omitted.
View Solution
MISCELLANEOUR EXERCISE : 15 questions and complete solutions for chapter STATISTICS of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 MATHS STATISTICS
- EXERCISE 5.1
- EXERCISE 5.2
- EXERCISE 5.3
- LATEST EXAM MCQS
- MISCELLANEOUR EXERCISE : 15
- NCERT EXEMPLAR PROBLEMS (FILLERS)
- NCERT EXEMPLAR PROBLEMS (OBJECTIVE TYPE QUESTIONS)
- NCERT EXEMPLAR PROBLEMS (SHORT ANSWER TYPE QUESTIONS)
- PRACTICE WORK
- QUESTION OF MODULE (KNOWLEDGE TEST)
- TEXTBOOK BASED MCQS
- TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK