Complete Solutions to EXAMPLE of chapter INTRODUCTION TO THREE DIMENSIONAL GEOMETRY of Class 11 book with complete answers and questions

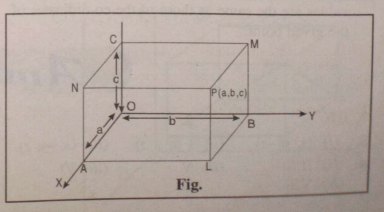
In the figure, if P is (a, b, c), find the co-ordinates of A, B, C and L, M, N.

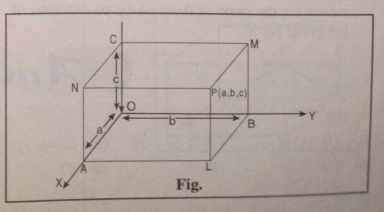
In the figure, if P is (2, 4, 5), find the co-ordinates of N.

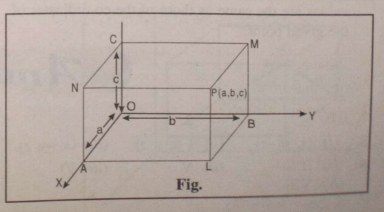
In the figure, find the co-ordinates of the reflection (image) of P in the XY-plane.

Name the octant in which the following points lie : (1, 2, 3).

Name the octant in which the following points lie : (4,-2,3).

Name the octant in which the following points lie : (4,-2,-5).

Name the octant in which the following points lie : (4, 2, - 5) .

Name the octant in which the following points lie : (- 4, 2, - 5).

Name the octant in which the following points lie : (-4, 2, 5).

Name the octant in which the following points lie : (- 3, -1, 6).

Name the octant in which the following points lie : (2, - 4, - 7).

Find the distance between points : A(2,3,5) and B (4, 3, 1).

Find the value of x, so that the point (6,5,-3) is at a distance of 13 units from the point (x,-7,0).

Find the point on the Y-axis, which is equidistant from the points (3, 1, 2) and (5, 5, 2).

Using distance formula, show that the points A(-3, 2, 4), B(- 1, 5, 9) and C (1, 8, 14) are collinear.

Show that the triangle with vertices (6, 10, 10), (1, 0, - 5) and (6, - 10, 0) is a right-angled triangle.

Show that the points : A (0,1,2),B(2,-1,3) and C (1,-3,1) are vertices of an isosceles right angle triangle.

Show that the points (5, - 1, 1),(7, - 4, 7), (1, - 6, 10) and (- 1, -3, 4) are the vertices of a rhombus.

Find the co-ordinates of the point, which is equidistant from four points (0, 0, 0), (a, 0, 0), (0, b, 0) and (0, 0, c).

Find the equation of the set of points P such that its distances from the points A (3, 4, - 5) and B (- 2, 1, 4) are equal.

Find the co-ordinates of the point, which divides the line segment joining the points (5, 4, 2) and (-1, -2, 4) in the ratio : 2:3 .

Find the co-ordinates of the point, which divides the line segment joining the points (5, 4, 2) and (-1, -2, 4) in the ratio : 2:3 .

Find the co-ordinates of the point R, which divides [PQ] externally in the ratio 2: 1 and verify that Q is the mid-point of PR.

A point R with x-co-ordinate 4 lies on the line segment joining the points P(2,-3,4) and Q(8,0,10). Find the co-ordinate of the point R.

Find the ratio in which the plane `3x+ 4y-5z =1` divides the line joining the points (-2, 4, -6) and (3, - 5, 8).

Using section formula, prove that the three points (- 4, 6, 10), (2, 4, 6) and (14,0,-2) are collinear.

A (3, 2, 0), B(5, 3, 2), C(- 9, 6, -3) are three points forming a triangle. AD, the bisector of `anlge BAC` meets [BC] at D. Find the co-ordinates of D.

Show that the points (3, -1, -1), (5,-4, 0), (2, 3, -2) and ( 0, 6, -3) are the vertices of a parallelogram*.

Find the third vertex of the triangle whose centroid is (7, -2, 5) and whose other two vertices are (2, 6,-4) and (4, -2, 3).

Prove that the lines joining the vertices of a tetrahedron to the centroids of the opposite faces are concurrent.