Complete Solutions to EXERCISE of chapter INTRODUCTION TO THREE DIMENSIONAL GEOMETRY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | INTRODUCTION TO THREE DIMENSIONAL GEOMETRY |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
A point is on x-axis. What are its y-co-ordinate and z-co-ordinate ?
View SolutionA point is in the XZ-plane. What can you say about its y-co-ordinate ?
View SolutionIn the figure, find the reflection of P(x, y, z) in the: XY-plane.
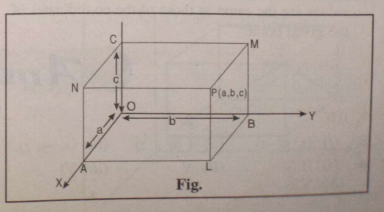
View SolutionIn the figure, find the reflection of P(x, y, z) in the: YZ-plane.
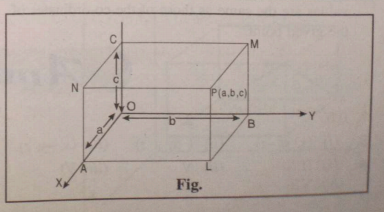
View SolutionIn the figure, find the reflection of P(x, y, z) in the: ZX-plane.
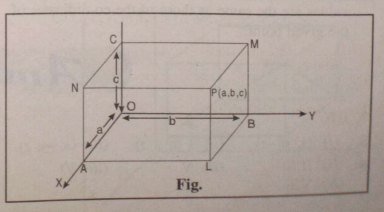
View SolutionFind the octant in which the following points lie :
(- 3, 1, 2).
View SolutionFind the octant in which the following points lie :
(3, 1, - 2) .
View SolutionFind the octant in which the following points lie :
(- 3, 1, - 2) .
View SolutionFind the octant in which the following points lie :
(- 3, - 1, - 2).
View SolutionWrite the perpendicular distance of the point (x, y, z) from the three co-ordinate planes. (Assume that x, y, z are all positive)
View SolutionThe co-ordinates of a point are (1, -2, 7). Find the co-ordinates of the seven points whose absolute values are the same as those of the co-ordinates of the given point.
View SolutionWrite the co-ordinates of the feet of perpendicular from the point (a, b, c) on the co-ordinate axes.
View SolutionFind the image of the point in the specified plane :
(5,4,-3) in the XY-plane.
View SolutionFind the image of the point in the specified plane :
(-2,0,0) in the XY-plane.
View SolutionFind the image of the point in the specified plane :
(-3, 4, 7) in the YZ-plane.
View SolutionFind the image of the point in the specified plane :
(- 7, 2, -1) in the ZX-plane.
View SolutionFind the image of the point in the specified plane :
(- 4,0, 1) in the ZX-plane.
View SolutionFind the perpendicular distances of the point P (a, b, c) from the co-ordinate axes.
View SolutionPlanes are drawn parallel to co-ordinate planes through the points (3, 0, -1) and (-2, 5, 4). Find the lengths of the edges of the parallelopiped so formed.
View SolutionFill in the blanks :
The x-axis and y-axis, taken together, determine a plane, known as ........ .
View SolutionThe co-ordinate of points in the xy-plane are of the form ……..
View SolutionCo-ordinate planes divide the space into …….. Octants.
View SolutionFind the distance between the points :
(1, -3,4) and (- 4, 1, 2) .
View SolutionFind the distance between the points :
(- 3,7,2) and (2, 4, - 1) .
View SolutionFind the distance between the points :
(- 1,3, - 4) and (1, - 3, 4) .
View SolutionFind the distance between the points :
(2,-1,3) and (- 2,1,3).
View SolutionFind the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, - 1).
View SolutionFind the locus of a point, which is equidistant from the points (-1, 2, 3) and (3, 2, 1).
View SolutionFind the locus of a point, which moves so that its distance from (1, 2, 3) is four times its distance from YZ-plane.
View SolutionFind the points on the X-axis, which are at a distance of `2 sqrt6` units from the point (1,-2, 3).
View SolutionFind the co-ordinate of a point on y-axis which are at a distance of `5sqrt(2)` from the point P(3,-2,5).
View SolutionFind k so that the distance between the points (7, 1, - 3) and (4,5, k) be 13 units.
View SolutionProve that the following points are collinear :
(- 2, 3, 5), (1, 2, 3), (7, 0, - 1).
View SolutionProve that the following points are collinear :
(2, - 1, 3), (4, 3, 1), (3, 1, 2).
View SolutionProve that the following points are collinear :
(6, - 7, - 1), (2, - 3, 1), (4, -5, 0).
View SolutionProve that the following points are collinear :
(- 1, 4, - 2), (2, -2, 1), (0, 2,-1).
View SolutionProve that the following points are collinear :
(3,-5,1), (-1, 0, 8), (7,-10, - 6).
View SolutionProve that the following points are collinear :
(2,- 4,1), (4, 4, 3), (3, 0, 2).
View SolutionProve that the following points are collinear :
(4, 5, - 5), (0, - 11, 3), (2, - 3, -1).
View SolutionProve that the following points are collinear :
(1, 2, 3), (4, 0, 4), (-2, 4, 2).
View SolutionProve that the following points are collinear :
(- 2, 3, 5), (1, 2, 3), (7, 0, - 1).
View SolutionVerify that the points (3, - 2, 4), (1, 0, - 2) and (-1,2, - 8) are collinear.
View SolutionShow that the triangle with vertices (0, 7, 10), (-1, 6, 6) and (- 4, 9, 6) is right-angled.
View SolutionAre the points A (3, 6, 9), B (10, 20, 30) and C (25,- 41, 5) the vertices of a right-angled triangle ?
View SolutionProve that the points (0, 7,-10), (1, 6,-6) and (4,9, - 6) are the vertices of an isosceles triangle.
View SolutionShow that A(a,b,c),B(b,c,a) and C(c,a,b) are the vertices of an equilateral triangle.
View SolutionShow that the points : (0,4,1),(2,3,-1),(4,5,0) and (2,6,2) are vertices of square.
View SolutionShow that the points `(1, 2, 3), (-1, -2, -1), (2, 3, 2) and (4, 7, 6)` are the vertices of a parallelogram.
View SolutionShow that the points (-1,2,1), (1,-2,5), (4,-7,8) and (2,-3,4) are vertices of a parallelogram.
View SolutionShow that the points (5, - 1, 1),(7, - 4, 7), (1, - 6, 10) and (- 1, -3, 4) are the vertices of a rhombus.
View SolutionFind the equation of the set of points P, the sum of whose distance from A(4,0,0) and B(-4,0,0) is equal to 10.
View SolutionIf A and B be the points (3,4,5) and (-1,3,-7) respectively, find the equation of the set of point P such that `PA^2+PB^2=k^2`, where k is constant.
View SolutionFind the co-ordinates of the point, which is equidistant from four points (0, 0, 0), (a, 0, 0), (0, b, 0) and (0, 0, c).
View SolutionFind the co-ordinates of the point, which is equidistant from four points (0, 0, 0), (a, 0, 0), (0, b, 0) and (0, 0, c).
View SolutionShow that (-1, 4, -3) is the circumcentre of the triangle formed by the points (3, 2, -5), (-3, 8, -5) and (- 3, 2, 1).
View SolutionFind the co-ordinates of the point, which divides the join of (-2, 3, 5) and (1, - 4, - 6) in the ratio 2 : 3 internally.
View SolutionFind the co-ordinates of the point, which divides the join of (-2, 3, 5) and (1, - 4, - 6) in the ratio 2 : 3 externally.
View SolutionFind the co-ordinates of the points, which divide the join of the points (1, -2, 3) and (3, 4, -5) in the ratio 2 : 3 internally.
View SolutionFind the co-ordinates of the points, which divide the join of the points (1, -2, 3) and (3, 4, -5) in the ratio 2 : 3 externally.
View SolutionFind the co-ordinates of the mid-point of the join of the points A (3, 5, 7) and B(-3,-3, 1).
View SolutionFind the coordinates of the points which trisect the line segment joining the points P(4,2,-6) and Q(10,-16,6).
View SolutionFind the co-ordinates of the point R, which divides the join of P (0, 0, 0) and Q (4, -1, -2) in the ratio 1 : 2 externally and verify that P is the mid-point of [RQ].
View SolutionFind the ratio in which the line joining the points (- 2, 4, 5) and (3,- 5, 4) is divided by xz plane.
View SolutionFind the ratio in which the line joining the points (- 2, 4, 5) and (3,- 5, 4) is divided by xz plane.
View SolutionFind the ratio in which the line segment joining the points (4, 8, 10) and (6, 10, -8) is divided by yz-plane.
View SolutionFind the ratio in which yz-plane divides the line segment formed by Joining the points (-2, 4, 7) and (3,-5, 8).
View SolutionFind the ratio in which `2x+3y+5z=1` divides the line joining the points `(1, 0, -3) and (1, -5, 7).`
View SolutionGiven that A (3, 2,-4), B(5, 4, -6) and C(9, 8, -10) are collinear. Find the ratio in which B divides [AC].
View SolutionUsing Section formula, show that the points A (2,- 3, 4), B (-1, 2, 1) and C `(0,1/3,2)` are collinear.
View SolutionGiven that p(3,2,-4) , Q (5,4, -6) and R (9,8,-10) are collinear find the ratio in which Q divides PR
View SolutionIf the mid points of the sides of a triangle are `(1, 5, -1), (0, 4, -2) and (2, 3, 4).` Find its vertices.
View SolutionShow that the points (-1,2,1), (1,-2,5), (4,-7,8) and (2,-3,4) are vertices of a parallelogram.
View SolutionThree vertices of parallelogram ABCD are A(3,-1,2), B(1,2,-4), C(-1,1,2). Find the co-ordinate of the fourth vertex.
View SolutionShow that the points A(1, 2, 3,), B (-1, -2. -1), C(2, 3, 2) and D(4, 7, 6) are the vertices of parallelogram ABCD but it is not a rectangle.
View SolutionThe vertices of triangle are `A(1,1,2),B(4,3,1) and C(2,3,5)`. A vector representing the internal bisector of the `angleA` is
View SolutionFind the lengths of the medians of the triangle A (0, 0, 6), B (0, 4, 0) and C (6, 0, 0).
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinats of the point C.
View SolutionIf the origin is the centroid of the triangle PQR with vertices P(2a,2,6), Q(-4,3b,-10) and R(8,14,2c), then find the value of a,b and c.
View SolutionPlanes are drawn through the points (5, 0, 2) and (3, - 2, 5) parallel to the co-ordinates planes. Find the lengths of the edges of the rectangular parallelopiped so formed.
View SolutionProve that the lines joining the vertices of a tetrahedron to the centroids of the opposite faces are concurrent.
View SolutionFind the lengths of the edges of the rectangular parallelopiped formed by planes drawn through the points (1, 2, 3) and (4, 7, 6) parallel to the co-ordinate planes.
View SolutionVerify that (0, 7, 10) , (-1,6,6) and (-4, 9,6) are the vertices of a right angled triangle.
View SolutionShow that the points : (4, 7, 8), (2, 3, 4), (- 1, - 2, 1), (1, 2, 5) are the vertices of a parallelogram.
View SolutionShow that the points (5, - 1, 1),(7, - 4, 7), (1, - 6, 10) and (- 1, -3, 4) are the vertices of a rhombus.
View SolutionIf A and B be the points (3,4,5) and (-1,3,-7) respectively, find the equation of the set of point P such that `PA^2+PB^2=k^2`, where k is constant.
View SolutionFind the co-ordinates of the point, which is equidistant from four points (0, 0, 0), (a, 0, 0), (0, b, 0) and (0, 0, c).
View Solution
EXERCISE questions and complete solutions for chapter INTRODUCTION TO THREE DIMENSIONAL GEOMETRY of MODERN PUBLICATION of Class 11