Complete Solutions to Exercise of chapter Moment of Inertia of Class 11 book with complete answers and questions

Define moment of inertia

What is the moment of inertia of a ring

Define radius of gyration.

What do you mean by radius of gyration? Derive an expression for it.

Define moment of inertia

Define radius of gyration.

What is physical significnce of moment of inertia?

Define moment of inertia

On what factors does the moment of inertia depend?

On what factors does the moment of inertia depend?

Explain, what do you mean by the moment of inertia of a body.

Define moment of inertia

Prove the theorem of parallel axes.

State Theorem of perpendicular axis.

Derive the expression for moment of inertia of a circular disc
about an axis passing through its centre and perpendicular to its plane

Derive the expression for moment of inertia of a circular disc
about an axis passing through its centre and perpendicular to its plane

Derive the expression for moment of inertia of a circular disc
about the diameter of the disc.

Derive the expression for moment of inertia of a circular disc
about an axis passing through its centre and perpendicular to its plane

State the two theorems of moment of inertia. Give an example of the application in each case.

Define perpendicular axis theorem of moment of inertia.

give the relation between moment of inertia and torque on a rigid body.

Which physical quantities are represented by the following ?
i) Product of moment of inertia and the angular velocity:
ii) Product of moment of inertia and the angular acceleration.

Establish the relation between torque and angular acceleration.

Find the relation between angular momentum and lever arm.

Deduce the relation between torque and moment of inertia.

Deduce the relation between torque and moment of inertia.

Derive the expression for angular momentum in three dimensions.

Derive relation between kinetic energy of rotation and moment of inertia.

Find an expression for the rotational kinetic energy of a body.

Derive relation between kinetic energy of rotation and moment of inertia.

Show that the moment of a body about the given axis of rotation is equal to twice of the kinetic energy of rotation of the body rotating with unit angular velocity.

Define moment of inertia

Derive a relation between angular momentum and torque.

In rotational motion power is the product of torque and -----

A body of moment of inertia I is rotating with an angular velocity `omega_1`, about a certain axis. Derive an expression for work done by a torque in increasing its angular velocity `omega_2` about the same axis of rotation.

State the principle of conservation of angular momentum.

Write the unit of angular momentum.

Define radius of gyration.

State the law of conservation of angular momentum.

State the principle of conservation of angular momentum.

State the principle of conservation of angular momentum.

A block is in limiting equilibrium on an inclined plane of angle theeta ,Then ,the coefficient of friction is :

Four small bodies A, B, C and D which can be considered as particles are connected by rods of negligible masses as shown in Fig. Find the M.I. of the system about an axis passing through A and perpendicular to the plane of diagram.

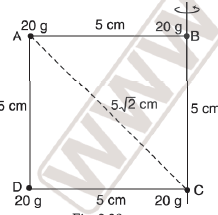
Four masses each of 2 kg are placed on a horizontal disc of negligible mass, which can be rotated about a vertical axis passing through its centre. If all the masses be equidistant from the axis and at the distance of 10 cm from it, what is moment of inertia of the whole system?

Find the moment of inertia of a rod of length 0.5 m and mass 0.2 kg about an axis passing through its centre and being perpendicular to its length.

Find the moment of inertia of a rod of length 0.5 m and mass 0.2 kg about an axis through one end of the rod, the axis being perpendicular to its length.

The mass of a straight uniform rod is 40 g. Find the length of the rod, whose moment of inertia about an axis passing through its centre and perpendicular to its length is `1,080 g cm^2`. Also calculate the radius of gyration of the rod about the same axis.

Find the moment of inertia of a rod of length 0.5 m and mass 0.2 kg about an axis passing through its centre and being perpendicular to its length.

Use the theorem of parallel axis to calculate moment of inertia of a disc of mass 400 g and radius 7 cm about an axis passing through its edge and perpendicular to the plane of the disc.

The moment of inertia of a thin rod about an axis passing through its centre and perpendicular to its length is `1,200 g cm^2`. If length of the rod is 20 cm, find its moment of inertia about an axis passing through its one end and perpendicular to its length.

Show that the radii of gyration of a circular ring and circular disc of the same radius about an axis passing through their centres and perpendicular to their plane are in the ratio `sqrt(2) : 1`

show that the radii of gyration of a circular disc and a circular ring of the same radius about a tangential axis in the plane of the ring is `sqrt5:sqrt6`

A torque of `10^(8)` dyne - cm is applied to a fly wheel of mass 10 kg and radius of gyration 50 cm. What is the resultant angular acceleration ?

A grindstone has a moment of inertia of `50 kg m^(2)`. A constant torque is applied and the grindstome is found to have a speed of 150 rpm 10 s after starting from rest. Calculate the torque applied.

A constant torque of 20 N m is exerted on a pivoted wheel for 10 seconds during which, the angular velocity of the wheel changes from zero to 100 r.p.m. When torque is removed, it is stopped by friction in 110s. Find the M.I. of the wheel

A constant torque of 20 N m is exerted on a pivoted wheel for 10 seconds during which, the angular velocity of the wheel changes from zero to 100 r.p.m. When torque is removed, it is stopped by friction in 110s. Find the M.I. of the wheel

A constant torque of 20 N m is exerted on a pivoted wheel for 10 seconds during which, the angular velocity of the wheel changes from zero to 100 r.p.m. When torque is removed, it is stopped by friction in 110s. Find the M.I. of the wheel

A symmetrical body is rotating about its axis its moment of inertia about the axis of rotation being `1kgm^-2` and its rate of rotation 2 r.p.s. What is the angular momentum?

A symmetrical body is rotating about its axis its moment of inertia about the axis of rotation being `1kgm^-2` and its rate of rotation 2 r.p.s. What is the angular momentum?

How much tangential force would be needed to stop the earth in one year, if it were rotating with angular velocity of `7.3 xx 10^(-5)rad s^(-1)`? Given the moment of inertia of the earth =`9.3 xx 10^(37)kg m^(2)` and radius of the earth =`6.4 xx 10^(6) m`

An automobile moves on a road with a speed of `54kmh−1` .The radius of its wheels is 0.45 m. What is the torque transmitted by its brakes to a wheel, if the vehicle is brought to rest in 15 s. The moment of inertia of the wheel about its axis of rotation is `3 kg m^2`

A 40 kg flywheel in the form of a uniform circular disc 1 m in radius is making 120 revolutions per minute. Calculate the angular momentum. Given that M.I. of a disc=`1/2 xx mass xx radius^2`

Calculate the angular momentum of the spherical earth rotating about its own axis, if the mass of earth is5.98x10^24 kg and mean radius of the earth is 6.38 x 10^6 m. Given that M.I. of a sphere =`2/5 xx mass xx radius^2`

A rod revolving 60 times in a minute about an axis passing through an end at right angles to the length has kinetic energy of 400 J. Find moment of inertia of the rod.

A disc of mass 200 kg and radius 0-5 m is rotating at the rate of 8 r.p.s. Find the work done to bring the disc to rest. If the disc is stopped in 11 rotations, calculate the breaking torque.

A solid circular disc of mass 2500 kg and 0.5 m radius is rotating about an axis passing through its centre and perpendicular to its plane making 120 r.p.m. Calculate its kinetic energy.

A solid circular disc of mass 2500 kg and 0.5 m radius is rotating about an axis passing through its centre and perpendicular to its plane making 120 r.p.m. Find the torque required, if the disc is brought to rest in 2 s.

The earth has a mass of `6 xx 10^24 kg` and a radius of `6.4 xx 10^6 m`. Calculate the amount of work done, if its rotation were to be slowed down so that the duration of the day becomes 30 h.

Calculate the angular momentum and the rotational kinetic energy of the earth about its own axis. How long could this amount of energy supply 1 kW power to each of `3.5 x 10^9` persons on earth? Given, mass of the earth = `6.0 xx10^24 kg`, radius of the earth = `6.4 × 100 m`.

A disc of mass 5 kg and radius 0.5 m rolls on the ground at the rate of `10 ms^-1` Calculate the kinetic energy of the disc.

A solid sphere is rolling on a frictionless plane surface about its axis of symmetry. Find the ratio of its rotational energy to its total energy

A solid sphere is rolling on a frictionless plane surface about its axis of symmetry. Find the ratio of its translational energy to rotational energy

A star of mass 2 M, (two solar masses) and radius 10 ^6km rotates about its axis with an angular speed of 10^-6 rad s What is the angular speed of the star, when it collapses (due to inward gravitational forces) to a radius of 10^4 km?

If the earth suddenly contracts to one third of its present radius, calculate by how much would the day be shortened?

The sun rotates around itself once in 27 days. What will be the period of its revolution, if the sun were to expand twice its present radius? Consider the sun to be a sphere of the uniform density.

A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ? Assume that there is no slipping.

A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ? Assume that there is no slipping.

A cylinder of mass 5 kg is rolling on a plane of inclination `45^@` Find the force of friction between the cylinder and the surface of the inclined plane.

A diatomic molecule consists of two atoms of masses `m_1` and `m_2`. The two atoms are separated by a distance from each other. Calculate the M.I of the system about an axis passing through the centre of mass of the system and perpendicular to the line joining the atoms.

Four sphere each of mass 10 kg and of radius 20 cm are placed at the four cornes of a square of side 100 cm. Calculate the moment of inertia of the system about an axis coinciding with side of the square (given moment of inertia of sphere `= 2/5 MR^2`)

A point mass is tied to one end of a cord, whose other end passes through a vertical hollow tube, caught in one hand The point mass is being rotated in a horizontal circle of radius 2 m with a speed of `4 ms^-1`. The cord is then pulled down, so that the radius of the circle reduces to 1 m Compute the new linear and angular velocities of the point mass and compare the kinetic energy under the final and initial states

A uniform solid sphere rolls on a horizontal surface at `20 ms^-1` It, then, rolls up a plane inclined at `30^@` to the horizontal. Find the height up to which the sphere will rise Friction losses may be neglected

The Fig. shows a loop track, whose lower part ends into a circular track of radius R and centre O. A small solid sphere of mass M rolls without slipping along the loop track from the end A at height 6 R from the bottom of the track. Calculate the horizontal and vertical forces acting on the sphere, when it rises up to the point P in level with the centre O of the circular part.

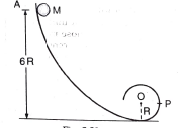
A metre stick is held vertically with one end on the floor and then allowed to fall.The speed of the other end when it hits the floor(assuming that the lower end does not slip) is :