Complete Solutions to Example of chapter Moment of Inertia of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Moment of Inertia |
| MODERN PUBLICATION | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The moment of inertia of a thin rod about an axis passing through its centre and perpendicular to its length is `1,200 g cm^2`. If length of the rod is 20 cm, find its moment of inertia about an axis passing through its one end and perpendicular to its length.
View SolutionThe moment of inertia of a circular ring about an axis passing through its centre and perpendicular to its plane is `200g cm^2` If radius of the ring is 5 cm, find the mass of the ring.
View SolutionThe moment of inertia of a uniform circular disc about a tangent of the disc in its own plane is given aby `5/4 MR^2`, where the symbols have their usual meanings. 4 Using this relation, find its M.I. about an axis through its centre and perpendicular to the plane.
View SolutionThe moment of inertia of a solid sphere about a tangent is `5/3MR^2`, where M is mass and R is radius of the sphere. Find the M.I. of the sphere about its diameter.
View SolutionA solid cylinder of moment of inertia `0.625 kg m^2` rotates about its axis with angular speed `100 rad s^-1`. What is the magnitude of the angular momentum of the cylinder about its axis ?
View SolutionIf the earth suddenly contracts, what will be the effect on the duration of the day? Substantiate your answer with proper reasoning.
View SolutionA sphere is rolling on a level surface. Find the ratio of the kinetic energy due to the translational motion to the total energy of the sphere.
View SolutionA ring, a disc and a sphere all of the same radius and mass roll down an inclined plane of inclination` theta` from the same height h. Which of the three reaches the bottom earliest?
View SolutionA ring, a disc and a sphere all of the same radius and mass roll down an inclined plane of inclination `theta` from the same height h. Which of the three reaches the bottom latest?
View SolutionThree mass points `m_1, m_2, m_3` are located at the vertices of an equilateral triangle of length a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through `m_1`
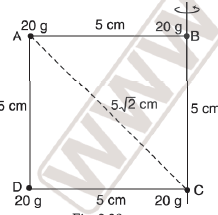
View SolutionFour small bodies A, B, C and D which can be considered as particles are connected by rods of negligible masses as shown in Fig. Find the M.I. of the system about an axis coinciding with rod BC.
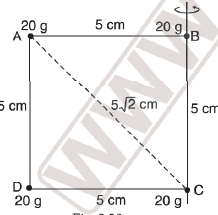
View SolutionFour small bodies A, B, C and D which can be considered as particles are connected by rods of negligible masses as shown in Fig. Find the M.I. of the system about an axis passing through A and perpendicular to the plane of diagram.
View SolutionCalculate the moment of inertia about a transverse axis through the centre of a disc, whole radius is 20 cm. Its density is `9 g cm^-3` and its thickness is 7cm.
View SolutionCalculate the M.L. of a uniform circular disc of mass 500 g and radius 10 cm about diameter of the disc
View SolutionCalculate the M.L. of a uniform circular disc of mass 500 g and radius 10 cm about the axis tangent to the disc'and parallel to its diameter
View SolutionCalculate the M.L. of a uniform circular disc of mass 500 g and radius 10 cm about the axis through the centre of the disce and perpendicular to its plane.
View SolutionWhat is the moment of inertia of a uniform circular disc of radius R and mass M about an axis passing through its centre and normal to disc? The moment of inertia of the disc about any of its diameter is given to be `(MR^2)/4`.
View SolutionWhat is the moment of inertia of a uniform circular disc of radius R and mass M about an axis passing through a point on its edge and normal to the disc? The moment of inertia of the disc about any of its diameter is given to be `(MR^2)/4`
View SolutionA constant torque of 400 Nm turns a wheel of moment of inertia `100 kg m^2` about an axis through its centre. Find the gain in angular velocity in 4 s
View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. It is making 240 r.p.m. What is the torque necessary to bring it to rest in 20 s? Assume that mass of the flywheel is concentrated at its rim.
View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. It is making 240 r.p.m.What is the torque necessary to bring it to rest in 20sec. If the torque is due to a force applied tangentially on the rim of the flywheel, what is magnitude of the force ? Assume that mass of the flywheel is concentrated at its rim.
View SolutionA cord is wound around the circumference of a wheel of diameter 0.3 m. The axis of the wheel is horizontal. A mass of 0.5 kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5 m in 4s, what is the angular acceleration of the wheel?
View SolutionA cord is wound around the circumference of a wheel of diameter 0.3 m. The axis of the wheel is horizontal. A mass of 0.5 kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5 m in 4s, find out the moment of inertia of the wheel.
View SolutionA circular ring of diameter 40cm and mass 1kg is rotating about an axis normal to its plane passing through the centre with a frequency of 10rps. calculate the angular momentum about the axis of rotation
View Solutioncompute the ratio of Earth's Orbital angular momentum and its rotational angular momentum about its axis. Given that radius of the earth is `6.4×10^6m` and the radius of the orbit of the earth = `1.5 × 10^11m`.
View SolutionEnergy of 484 J is spent in increasing the speed of a flywheel from 60 r.p.m. to 360 r.p.m. find moment of inertia of the flywheel.
View SolutionA particle performing uniform circular motion has angular momentum L. What will be its angular momentum if its angular frequency is halved and kinetic energy is doubled.
View SolutionA horizontal disc rotating about a vertical axis makes 100 revolutions per minute. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis. If the number of revolutions per minute is there by reduced to 90, calculate the moment of inertia of the disc.
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. What will be the angular velocity of the ring?
View SolutionA ball at the end of a string is being swung in a horizontal circle of radius 0.3m at a speed of `2.8ms^-1`. What will be the tangential speed of the ball if the string is pulled down so as to reduce the radius of the circle to 0.2m
View SolutionWhat will be the duration of the day of earth if the earth suddenly shrinks to `1/27` of its original volume, mass remains unchanged ?
View SolutionA cylindrical hoop is released from rest at a height of 0.7 m near the top of an inclined plane. If the hoop rolls down the inclined plane without slipping and there is no loss of energy due to friction, find the linear speed of the hoop, when it reaches the bottom of the plane? Given, moment of inertia of cylindrical hoop about its axis = M R^2.
View SolutionA solid cylinder rolls down an inclined plane. Its mass is 2kg and radius 0.1 m. If the height of the inclined plane is 4m, what is its rotational kinetic energy, when it reaches the foot of the plane? Assume that the surfaces are smooth. M.I of cylinder about its axis = `1/2 MR^2`
View SolutionA cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination `30^@`. The co-efficient of static friction `mus = 0.25`:- How much is the force of friction acting on the cylinder ?
View SolutionA cylinder of mass 10 kg is rolling perfectly on a plane of inclination `30^@` Find the force of friction between the cylinder and the surface of the inclined plane
View SolutionThree particles A, B and C, each of mass m, are connected to each other by three massless rigid rods to form a rigid equilateral triangular body of side l. This body is placed on a horizontal frictionless table and is hinged to it at the point A, so that it can move without friction about the vertical axis through A. The body is set into rotational motion on the table about A with a constant angular velocity `omega`. Find the magnitude of the horizontal force exerted by the hinge on the body.
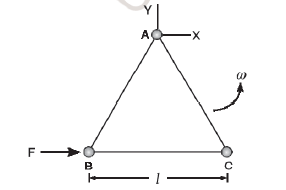
View SolutionThree particles A, B and C, each of mass m, are connected to each other by three massless rigid rods to form a rigid equilateral triangular body of side l. This body is placed on a horizontal frictionless table and is hinged to it at the point A, so that it can move without friction about the vertical axis through A. The body is set into rotational motion on the table about A with a constant angular velocity `omega`. Find the magnitude of the horizontal force exerted by the hinge on the body.

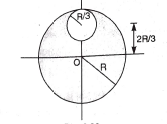
View SolutionFrom a circular disc of radius r and mass 9M a small disc of radius r/3 is removed from the disc as shown in figure. find the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through the point O.
View SolutionA rod of length l and mass m is hinged at point O. A small bullet of mass m hits the rod as shown in the figure. the bullet gets embedded in the rothed. find angular velocity of the system just after impact.

View SolutionA homogeneous rod AB of length L= 1.8 m and mass M is pivoted at the centre O in such a way that it can rotate freely in the vertical plane. The rod is initially in the horizontal position. An insect S of the same mass M falls vertically with speed `nu`on the point C, mid-way between the points O and B. Immediately after falling, the insect moves towards the end B, such that the rod rotates with a constant angular velocity `omega`. Determine the angular velocity.
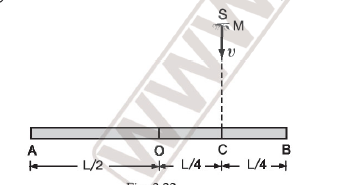
View SolutionA thin uniform bar lies on a frictionless horizonta surface and is free to move in any way on th surface. Its mass is 0.16 kg and length `sqrt3`meters. Two particless, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distane of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
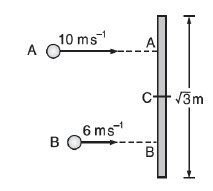
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground level and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown in fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass?
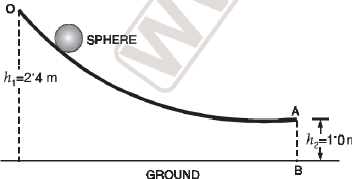
View SolutionA carpet of mass M made of inextensible material is rolled along its length in the form of a cylinder of radius R and kept on a rough floor. The carpet starts unrolling without sliding on the floor, when a negligibly small push is given to it. Calculate the horizontal velocity of the axis of a cylindrical part of the carpet, when its radius reduces to R/2.
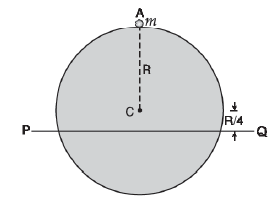
View SolutionA uniform circular disc has radius R and mass m. A particle also of mass m is fixed at a point A on the wedge of the disc as in fig. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then allowed to fall so that it starts rotating about PQ. Find the linear speed of the particle at it reaches its lowest position.
View SolutionDefine moment of inertia
View SolutionIs there any difference between moment of inertia and rotational inertia?
View SolutionWhy M.I. of called rotational inertia?
View SolutionDefine the term electric dipole moment. Is it a scalar or a vector quantity?
View SolutionDoes M.I. change with change of the axis of rotation?
View SolutionHow does M.I. change with speed of rotation.
View SolutionThe moment of inertia of a rigid body, depends upon
View SolutionWhat is physical significnce of moment of inertia?
View SolutionDefine radius of gyration.
View SolutionIs radius of gyration of a body a constant quantity?
View SolutionWhat is the moment of inertia of a ring
View SolutionWhat is the moment of inertia of a disc about their diameters?
View SolutionWhich physical quantities are represented by the following ?
i) Product of moment of inertia and the angular velocity:
ii) Product of moment of inertia and the angular acceleration.
View SolutionWhich physical quantities are represented by the following ?
i) Product of moment of inertia and the angular velocity:
ii) Product of moment of inertia and the angular acceleration.
View SolutionDerive an expression for kinetic energy of rotation.
View SolutionWhich physical quantities are represented by the following ?
i) Product of moment of inertia and the angular velocity:
ii) Product of moment of inertia and the angular acceleration.
View SolutionDefine radius of gyration.
View SolutionIs radius of gyration of a body a constant quantity?
View SolutionTwo satellites of equal masses are revolving around at different heights. Will their moment of inertia same or different?
View SolutionProve the theorem of parallel axes.
View SolutionDerive the expression for moment of inertia of a circular disc
about an axis passing through its centre and perpendicular to its plane
View SolutionIn a flywheel most of mass is concentrated at the rim. Explain why?
View SolutionTwo spheres of the same radii, one solid and other hollow are charged to the same potential, which one has greater charge?
View SolutionDerive relation between kinetic energy of rotation and moment of inertia.
View SolutionIf no external torque acts on a body. will its angular velocity remain conserved?
View SolutionThere is a stick half of which is woode half is of steel. It is pivoted at the wooden end and a force applied at the steel end at right angles to its length. Next it is pivoted at the steel end and the same force is app the wooden end. In which case is the angular accelen more and why?
View SolutionWhy is it more difficult to revolve a stone it to a longer string than by tying it to a shorter string?
View SolutionIf no external torque acts on a body. will its angular velocity remain conserved?
View SolutionHow will you distinguish between a hard boiled egg and a raw egg by spinning each on a table top?
View SolutionWhy angular speed of rotation of earth around the sun the increases, when it comes near the sun ?
View SolutionThe speed of inner layer of the whirl wind in a tornado is alarmingly high. Explain why
View SolutionHow does an ice-skater, a ballet dancer or an acrobat take advantage of the principle of conservation of angular momentum?
View SolutionHow the diver leaves the diving board, why he brings his hands and feet close together in order to make a sommersault?
View SolutionIf the ice on the polar caps of the earth melts, how will it affect the duration of the day? Explain.
View SolutionExplain how a cat is able to land gently on its feet after a fall taking the advantage of the law of conervation of angular momentu?
View SolutionExplain how a cat is able to land gently on its feet after a fall taking the advantage of the law of conervation of angular momentu?
View SolutionIf the angular momentum is conserved in a system whose MI is decreased, will its rotational KE be also conserved? Explain.
View SolutionGive the location of the centre of mass of a :- sphere.
View SolutionIn the HC1 molecule, the separation between the nuclei of the two atoms is about `1.27 overset@A` (`1 overset@A = 10^-10 m`). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
View SolutionA child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system ?
View SolutionShow that the area of the triangle contained between the vectors `veca` and `vecb` is one half of the magnitude of `veca xx vecb`.
View SolutionShow that `vecA. (vecB xx vecC)` is equal in magnitude to the volume of the parallelopiped formed on the three vectors `vecA, vecB and vecC`.
View SolutionFind the components along the x, y, z axes of the angular momentum 1 of a particle, whose position vector is r with components x, y, z and momentum is p with components `p_x,p_yand p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
View SolutionTwo particles, each of mass mand speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken.
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are `36.9^@` and `53.1^@` respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
View SolutionA car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be `2MR^2//5`, where M is the mass of the sphere and R is the radius of the sphere.
View SolutionGiven the moment of inertia of a disc of mass M and radius R about any of its diameters to be `MR^2//4`, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
View SolutionTorques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. Hie cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time.
View SolutionA solid cylinder of mass 20 kg rotates about its axis with angular speed `100 rad s^-1`. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
View SolutionA solid cylinder of mass 20 kg rotates about its axis with angular speed `100 rad s^-1`. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
View SolutionA child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of `40 rev//min`. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to `2//5` times the initial value ? Assume that the turntable rotates without friction.
View SolutionA child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value ? Assume that the turntable rotates without friction.
Show that the child's new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
View SolutionA rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
View SolutionTo maintain a rotor at a uniform angular speed of `200 rad s^-l`, an engine needs to transmit a torque of 180 N m. What is the power required by the engine ? (Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.
View SolutionFrom a uniform disk of radius R, a circular hole of radius `R//2` is cut out. The centre of the hole is at `R//2` from the centre of the original disc. Locale the centre of gravity of the resulting flat body.
View Solution
Example questions and complete solutions for chapter Moment of Inertia of MODERN PUBLICATION of Class 11