Complete Solutions to LEVEL-V of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| NARAYANA | LEVEL-V |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
A bead of mass m is fitted on to a rod and can move on it without friction. At the initial moment the bead is in the middle of the rod. The rod moves translationally in a horizontal plane with an acceleration a in a direction forming an angle `alpha` with the rod. Find the acceleration of the bead relative to the rod.

View SolutionA particle is projected with a velocity `8 m//sec` at an angle `45^(0)`, with the horizontal.What is the radius of curvature of the trajectory of the particle at the instant of `'1/4th'` of the time of ascent.
View SolutionA particle of mass in is moving in a circular with of constant radius `r` such that its contripetal accelenation `a_(c) ` is varying with time `t` as `a_(c) = K^(2) rt^(2)` where K` is a constant . The power delivered to the particles by the force action on it is
View SolutionA particle is projected with a velocity `'9 m//sec'` at an angle `45^(0)`, with the horizontal.What is the radius of curvature of the trajectory of the particle at the position `'x=R//3'` (R-Range of the projectile).
View SolutionThe figure shows th velocity and acceleration of a point like body at the initial moment of its motion. The acceleration vector of the body remain constant. The minimum radius of curvature of trajectory of the body is
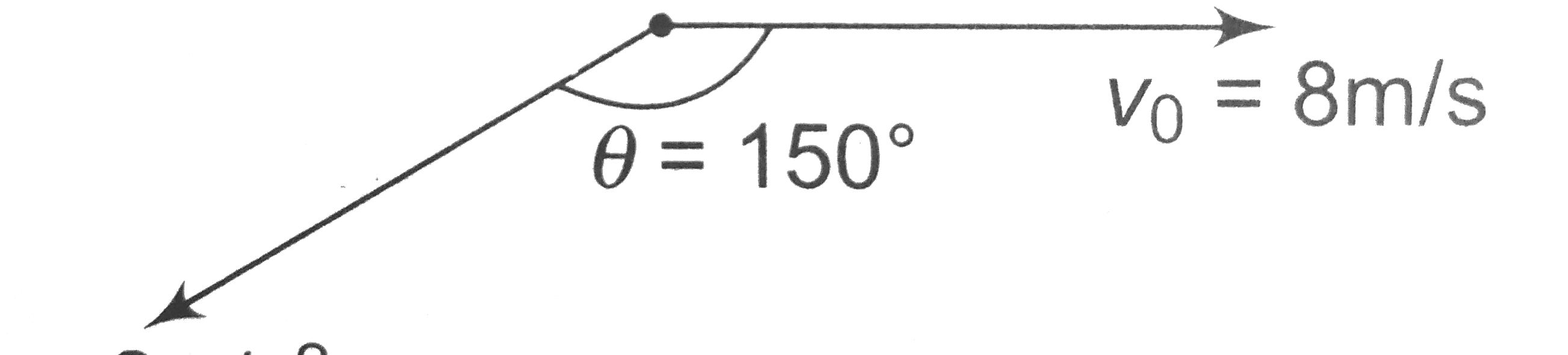
View SolutionA stone is thrown horizontally with a velocity of `10m//sec`. Find the radius of curvature of it’s trajectory at the end of `3 s` after motion began. `(g=10m//s^(2))`
View SolutionA small coin of mass `80g` is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration `alpha=2rad//s^(2)`. The coefficient of static friction between the coin and the disc is `mu_(s)=3//4` and cofficient of kinetic friction is `mu_(k)=0.5`. The coin is placed at a distance `r=1m` from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View SolutionWater of density `p` flows with a linear speed `v` through a horizontal rubber tube having the form of a ring of radius `R`. If the diameter of the tube is `d(ltlt R)`, find the tension in the rubber tube.
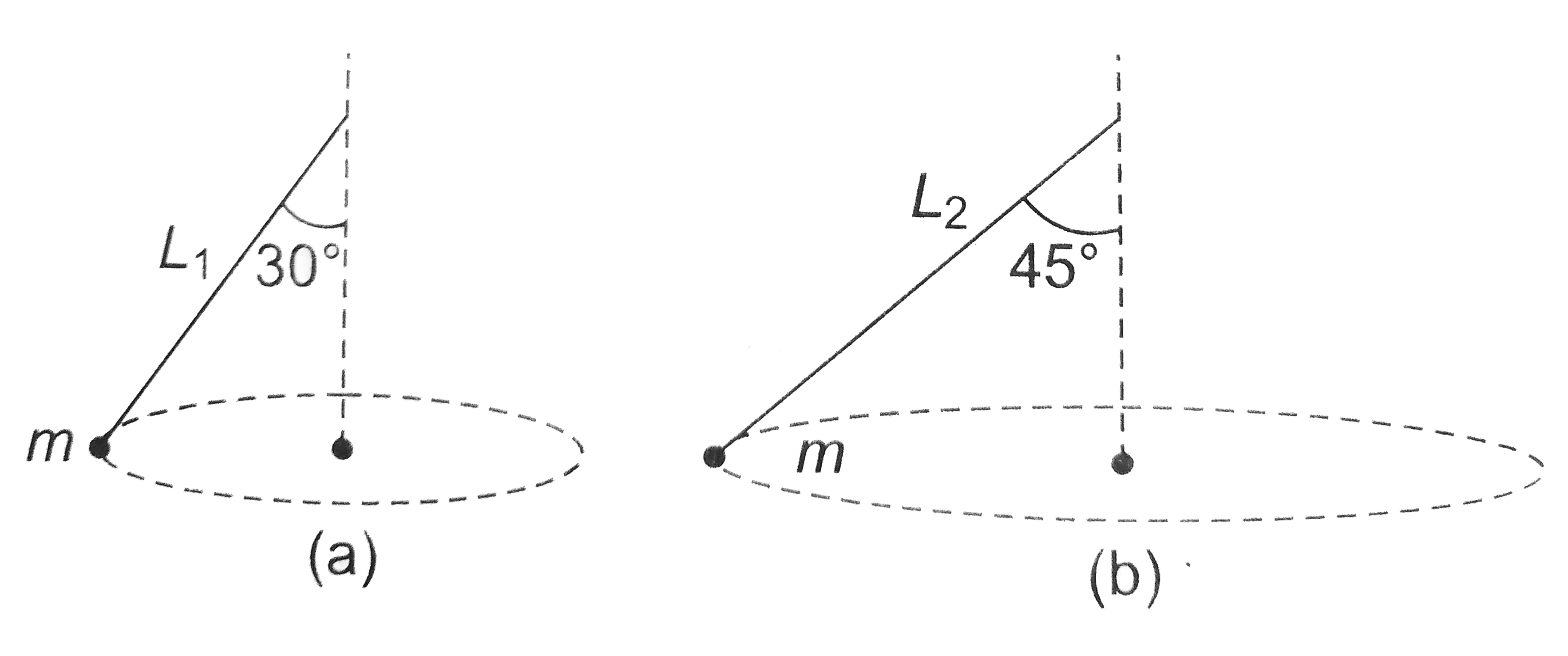
View SolutionTwo partical tied to different strings are whirled in a horizontal circle as shown in figure. The ratio of lengths of the string so that they complete their circular path with equal time priod is:
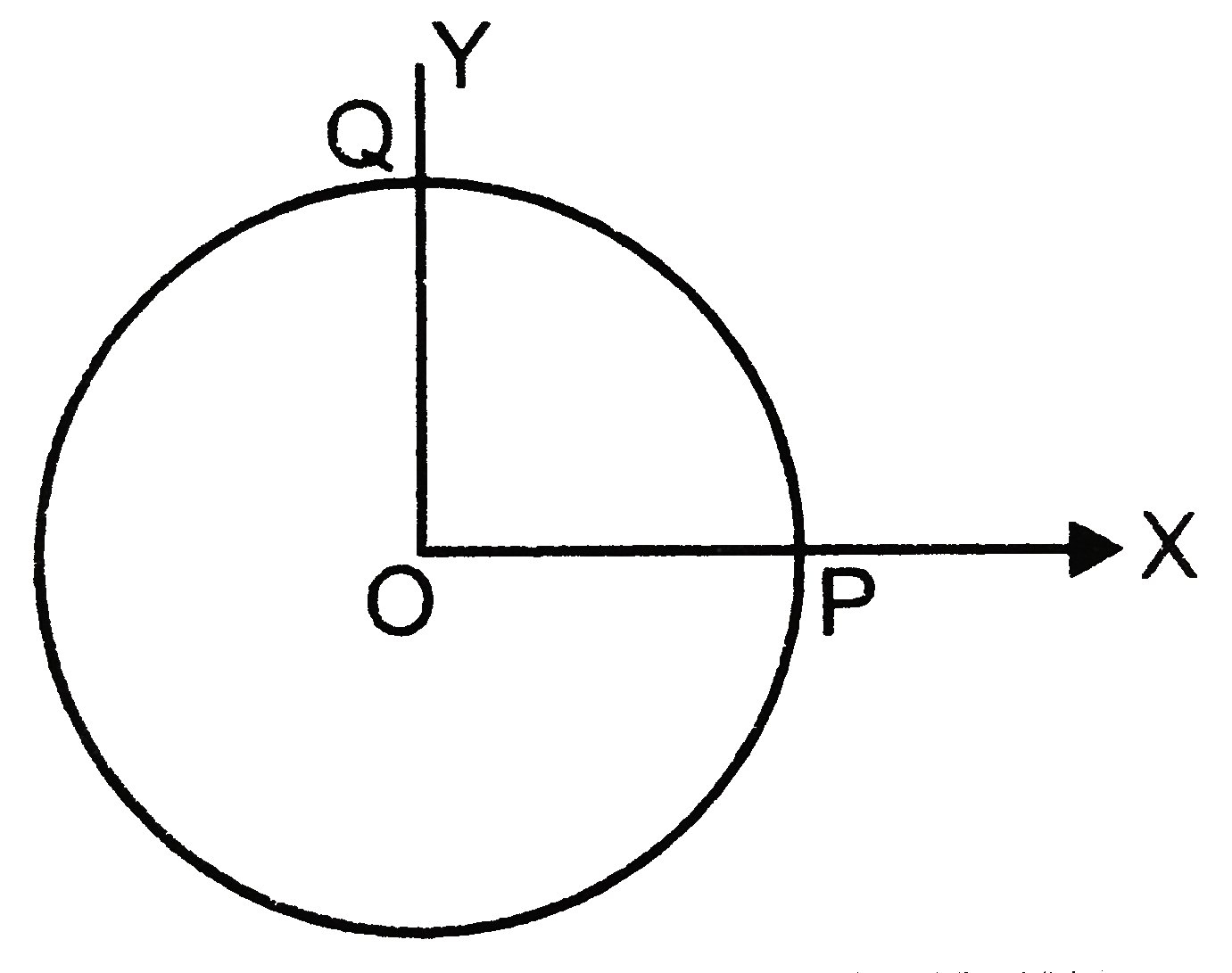
View SolutionA particle moves in a circle of radius ` 4.0 cm` clockwese at constant speed of ` 2cm S^(-1)` . If ` hat x` and ` hat y` ar unit accleration vectors along X- asis and Y-axis respectively, find the accleration of the particle at the instant half way between ` PQ. Fig. 2 ( d) . 38.
 .
.
View SolutionA reference frame attached to the earth
View SolutionA particle is moving along a circular path of radius of `R` such that radial acceleration of particle is proportional to `t^(2)` then
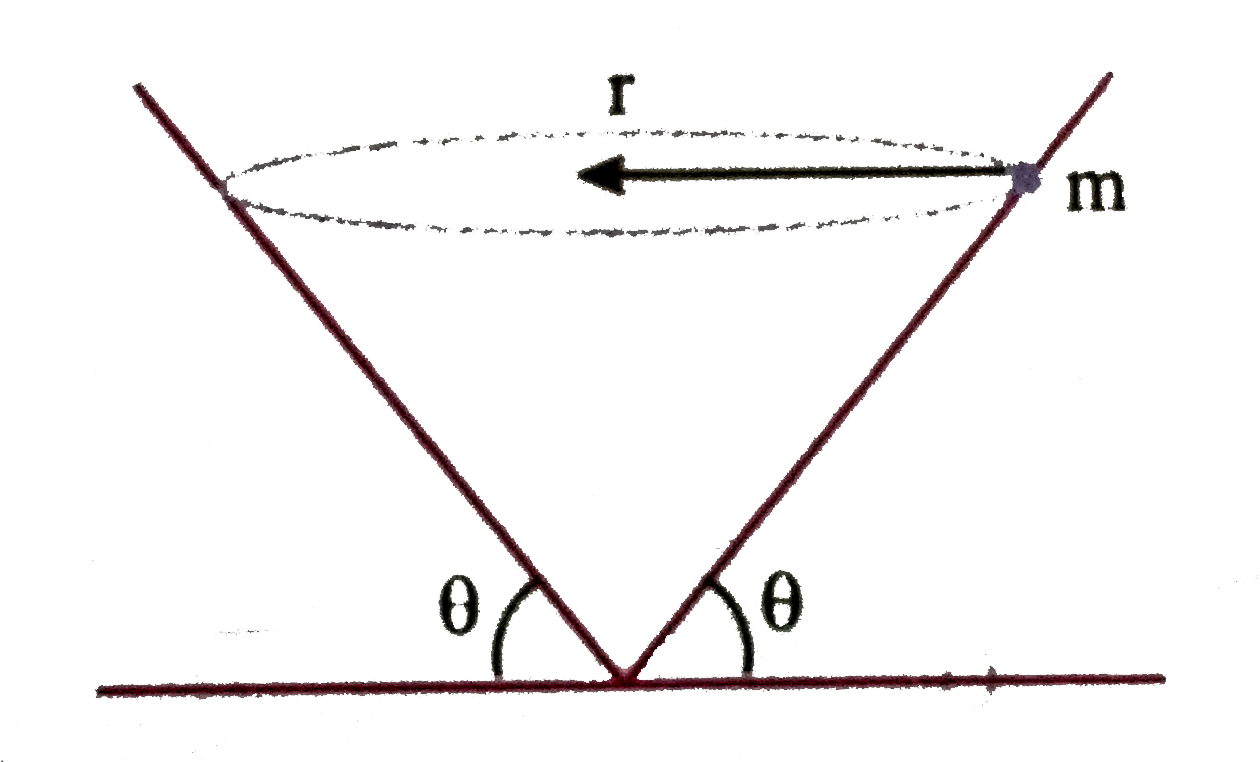
View SolutionA ball of mass `m` is rotating in a circle of radius `r` with speed `v` inside a smooth cone as shown in figure. Let `N` be the normal reaction on the ball by the cone, then choose the correct option:
View SolutionA Bead of mass `m` is attached to one end of a spring of natural length `'R'` and spring cosntant `'k=((sqrt3+1)mg)/R'`. The other end of the spring is fixed at point `'A'` on a smooth vertical ring of radius `'R'` as shown
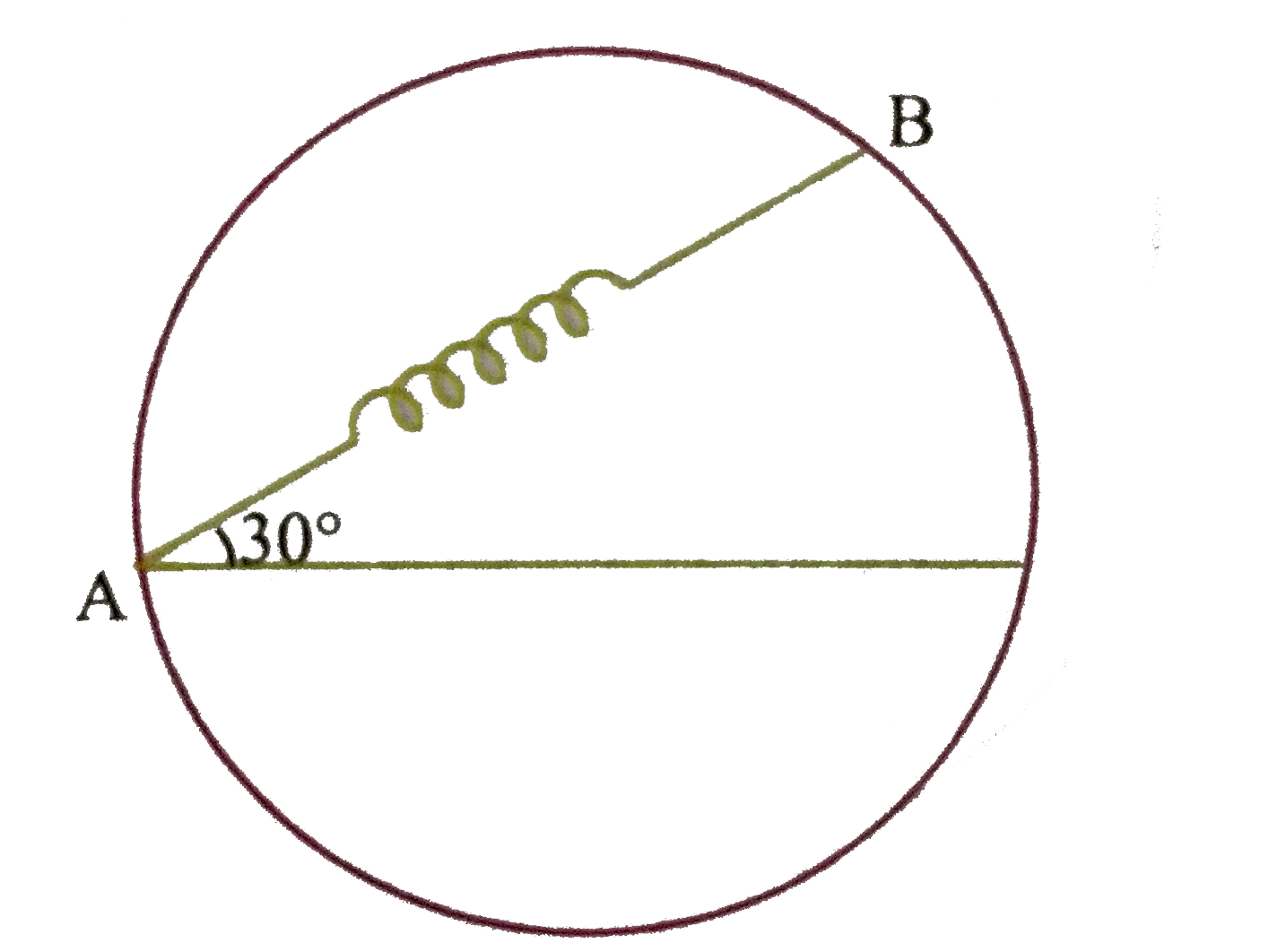
View SolutionAs shown in figure `AB` represents an infinite wall tangential to a horizontal semi circular track.`O` is a point source of light on the ground at the centre of the circle. A block moves along the circular track with speed `v` starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively `'V'` and `'a'` then,
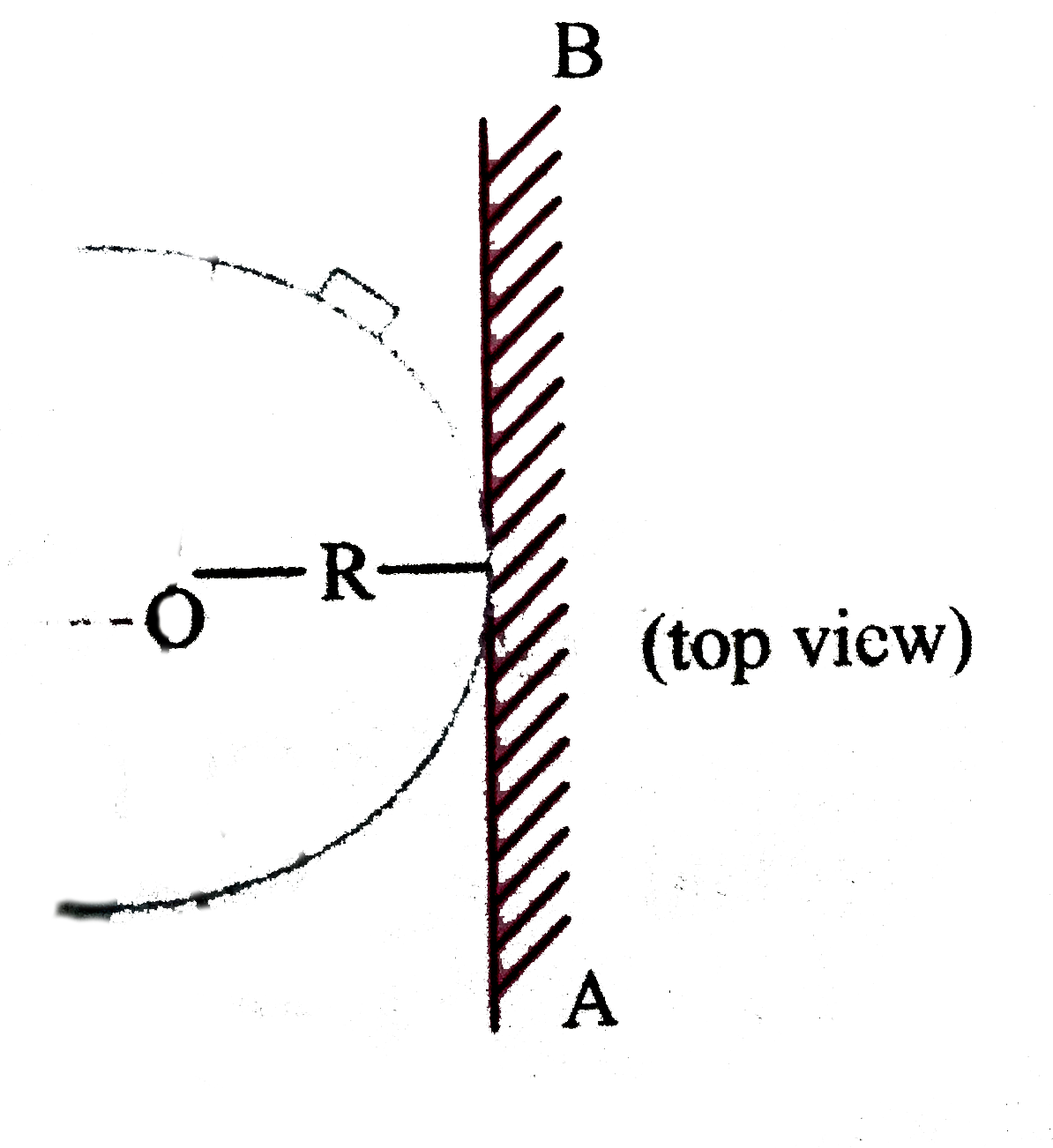
View SolutionIf `a_(r )` and `a_(t)` respresent radial and tangential acceleration, the motion of a particle will be circular is
View Solution`ABCDE` is a smooth iron track in the vertical plane. The sections `ABC` and `CDE` are quarter circles. Points `B` and `D` are very close to `C.M` is a small magnet of mass `m`. The force of attraction between `M` and the track is `F`, which is constant and always normal to the track. `M` starts from rest at `A`, then:
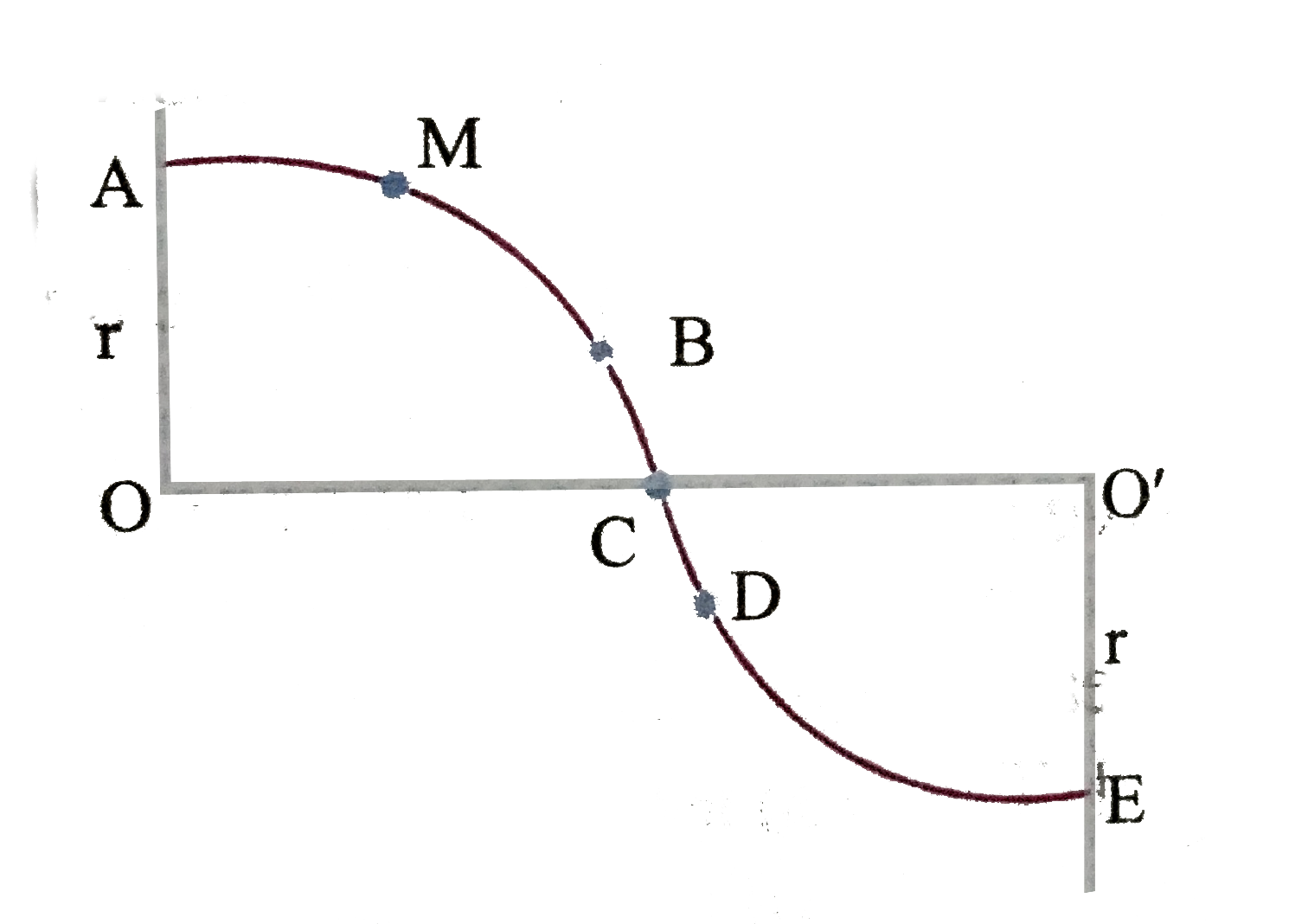
View SolutionWhen a cyclist turns on a circular path,the necessary centripetal force is provided by friction between the tyres and the road. If centripetal force is not provided by friction, then for the vehicle to move on circular path, the track is banked.
A cyclist going straight suddenly turns on wet road, then
View SolutionWhen a cyclist turns on a circular path,the necessary centripetal force is provided by friction between the tyres and the road. If centripetal force is not provided by friction, then for the vehicle to move on circular path, the track is banked.
The correct angle of banking for a curved smooth road of radius `120 m` for a speed of `108 km//h(g=10 ms^(-2))` is
View SolutionWhen a cyclist turns on a circular path,the necessary centripetal force is provided by friction between the tyres and the road. If centripetal force is not provided by friction, then for the vehicle to move on circular path, the track is banked.
If the speed of a vehicle is doubled, then for safety of vehicle
View SolutionA hemispherical bowl of radius `R=0.1m` is rotating about its own axis (which is verticle) with an angular velocity `omega`. A particle of mass `10^(-2)kg` on the smooth inner surface of the bowl is also rotating with the same `omega`. The particle is at a height `h` from the bottom of the bowl (a) obtain the relation betweemn `h` and `omega`. what is the minimum value of `omega` needed, in order to have a non-zero value of `h`? (b) it is desired to measure `g` using this set up, by measuring `h` accurately. assuming that `R` and `Omega` are known precisely and least count in the measurement of `h` is `10^(-4)m`, what is the minimum possible error `Deltag` in the measured value of `g`? `(g=10m//s^(2))`
View SolutionA hemispherical bowl of radius `R=0.1m` is rotating about its own axis (which is verticle) with an angular velocity `omega`. A particle of mass `10^(-2)kg` on the smooth inner surface of the bowl is also rotating with the same `omega`. The particle is at a height `h` from the bottom of the bowl (a) obtain the relation betweemn `h` and `omega`. what is the minimum value of `omega` needed, in order to have a non-zero value of `h`? (b) it is desired to measure `g` using this set up, by measuring `h` accurately. assuming that `R` and `Omega` are known precisely and least count in the measurement of `h` is `10^(-4)m`, what is the minimum possible error `Deltag` in the measured value of `g`? `(g=10m//s^(2))`
View SolutionA hemispherical bowl of radius `R=0.1m` is rotating about its own axis (which is verticle) with an angular velocity `omega`. A particle of mass `10^(-2)kg` on the smooth inner surface of the bowl is also rotating with the same `omega`. The particle is at a height `h` from the bottom of the bowl (a) obtain the relation betweemn `h` and `omega`. what is the minimum value of `omega` needed, in order to have a non-zero value of `h`? (b) it is desired to measure `g` using this set up, by measuring `h` accurately. assuming that `R` and `Omega` are known precisely and least count in the measurement of `h` is `10^(-4)m`, what is the minimum possible error `Deltag` in the measured value of `g`? `(g=10m//s^(2))`
View SolutionTwo blocks of mass `m_(1)=10kg` and `m_(2)=5kg` connected to each other by a massless inextensible string of length `0.3m` are placed along a diameter of the turntable. The coefficient of friction between the table and `m_(1)` is `0.5` while there is no friction between `m_(2)` and the table. the table is rotating with an angular velocity of `10rad//s`. about a vertical axis passing through its center `O`. the masses are placed along the diameter of the table on either side of the center `O` such that the mass `m_(1)` is at a distance of `0.124m` from `O`. the masses are observed to be at a rest with respect to an observed on the tuntable `(g=9.8m//s^(2))`.
(a) Calculate the friction on `m_(1)`
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on `m_(1)`.
View SolutionTwo blocks of mass `m_(1)=10kg` and `m_(2)=5kg` connected to each other by a massless inextensible string of length `0.3m` are placed along a diameter of the turntable. The coefficient of friction between the table and `m_(1)` is `0.5` while there is no friction between `m_(2)` and the table. the table is rotating with an angular velocity of `10rad//s`. about a vertical axis passing through its center `O`. the masses are placed along the diameter of the table on either side of the center `O` such that the mass `m_(1)` is at a distance of `0.124m` from `O`. the masses are observed to be at a rest with respect to an observed on the tuntable `(g=9.8m//s^(2))`.
(a) Calculate the friction on `m_(1)`
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on `m_(1)`.
View SolutionTwo blocks of mass `m_(1)=10kg` and `m_(2)=5kg` connected to each other by a massless inextensible string of length `0.3m` are placed along a diameter of the turntable. The coefficient of friction between the table and `m_(1)` is `0.5` while there is no friction between `m_(2)` and the table. the table is rotating with an angular velocity of `10rad//s`. about a vertical axis passing through its center `O`. the masses are placed along the diameter of the table on either side of the center `O` such that the mass `m_(1)` is at a distance of `0.124m` from `O`. the masses are observed to be at a rest with respect to an observed on the tuntable `(g=9.8m//s^(2))`.
(a) Calculate the friction on `m_(1)`
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on `m_(1)`.
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile.Projected with a speed `u=sqrt30` at angle `theta=60^(@)` with the horizontal at a point where the particle velocity makes an angle `theta//2` with the horizontal ?
View SolutionAn automobile moving with a speed of `10m//s` enters an unbanked curve of radius `r=50m`.If `g=10m//s`, the maximum valve of `mu` so as to safety negotiate the curve is `1//x`.Then `x=`
View Solution
LEVEL-V questions and complete solutions for chapter CIRCULAR MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11