Complete Solutions to LEVEL-VI of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| NARAYANA | LEVEL-VI |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
A small bead of mass `m` is carried by a circular hoop having center at `O` and radius `sqrt 2m` which rotates about a fixed vertical axis. The coefficient of friction between beed and hoop is `mu=0.5`. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop. `(g=10m//s^(2))`

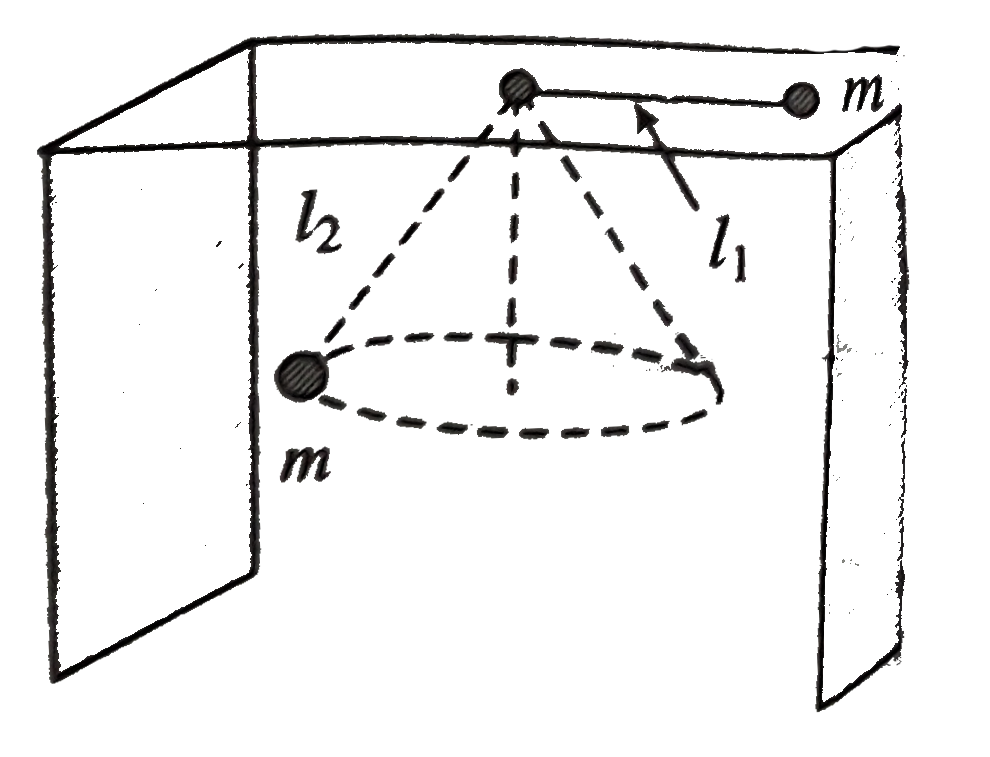
View SolutionTwo identical particles are attached at the end of a light string which passes through a hole at the center of a table One of the partical is made to move in a circle on a table with angular velocity `omega_(1)` and the ther is made a move is a horizontal `omega_(2)` if `l_(1)`and `l_(2)` are the length the table , than in order that particle under down the table neither moves down nor move up the ratio` l_(1)//l_(2)` is
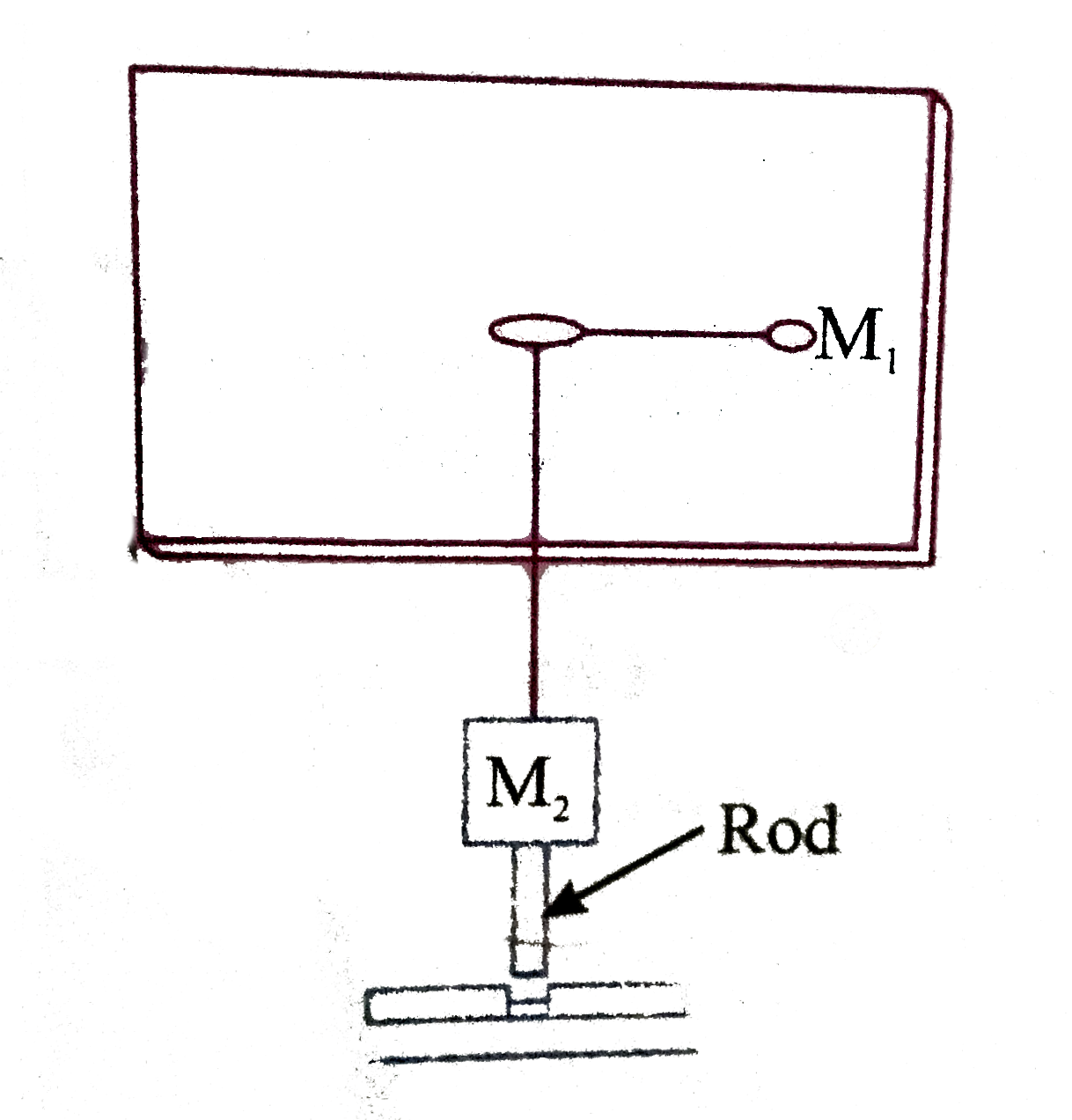
View SolutionFor the arrangement in the Figure, the particle `M_(1)` attached to one end of string which moves on a horizantal table in a circle of radius `l/2` (where `l` is the length of the string) with constant angular speed `omega`. The other end of the string attached to to mass `M_(2)` which rest on a vertical rod. When the rod collapse, the acceleration of mass `M_(2)` at that instant
View SolutionTwo particles `A` and `B` separated by a distance `2R` are moving counter clockwise along the same circular path of radius `R` each with uniform speed `v`. At time `t=0`, `A` is given a tangential acceleration of magnitude `a = (32v^(2))/(25piR)` in the same direction of initial velocity
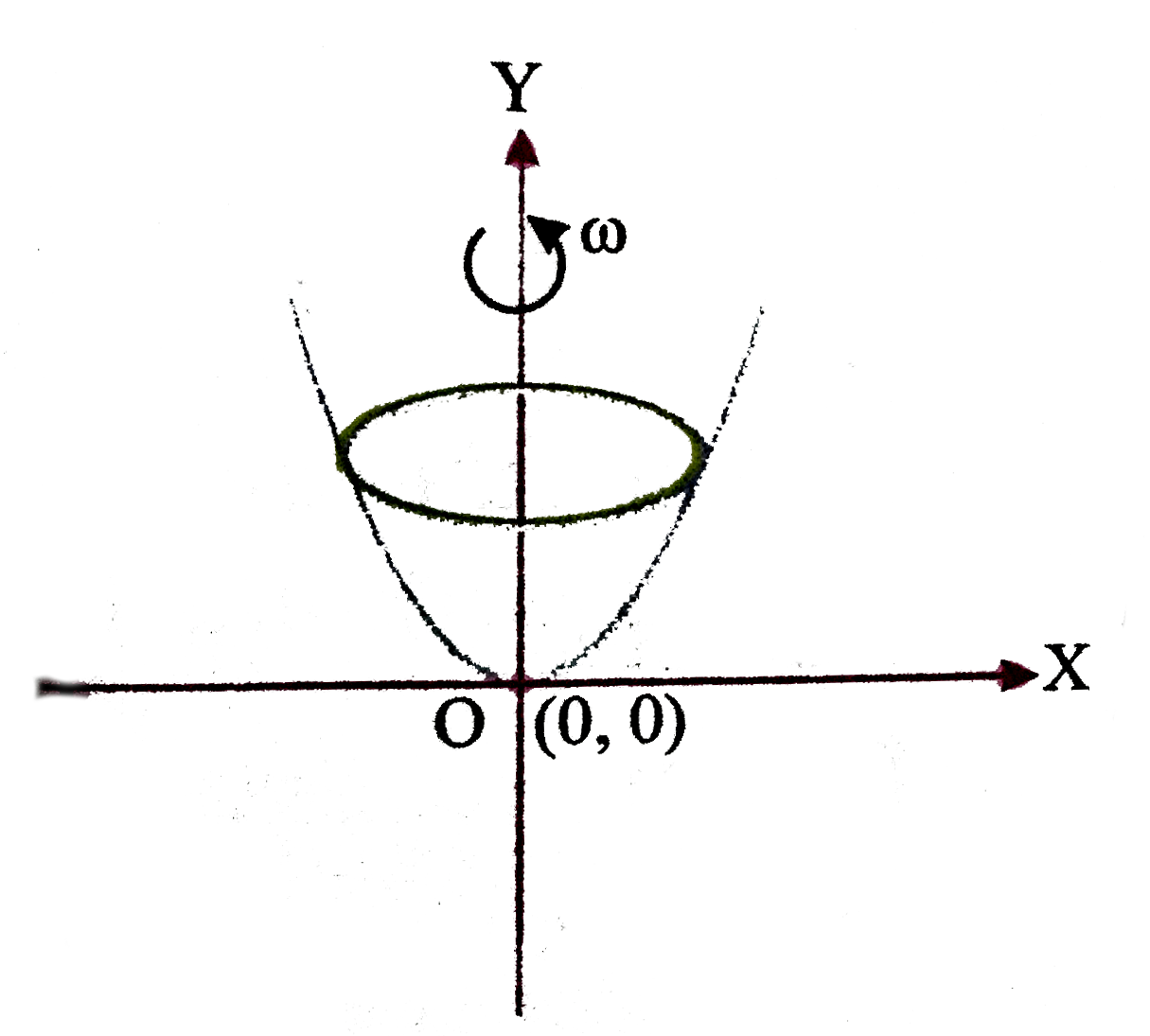
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is `x^(2) =4ay`. The wire frame is fixed and the bead is released from the point `y=4a` on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by `y=a` is

View SolutionA mass 1kg attached to the end of a flexible rope of diameter `d = 0.25 m`is raised vertically by winding the rope on a reel as shown. If the reel is turned uniformly at the rate of `2r.p.s.` What is the tension in rope. The inertia of rope may be neglected.
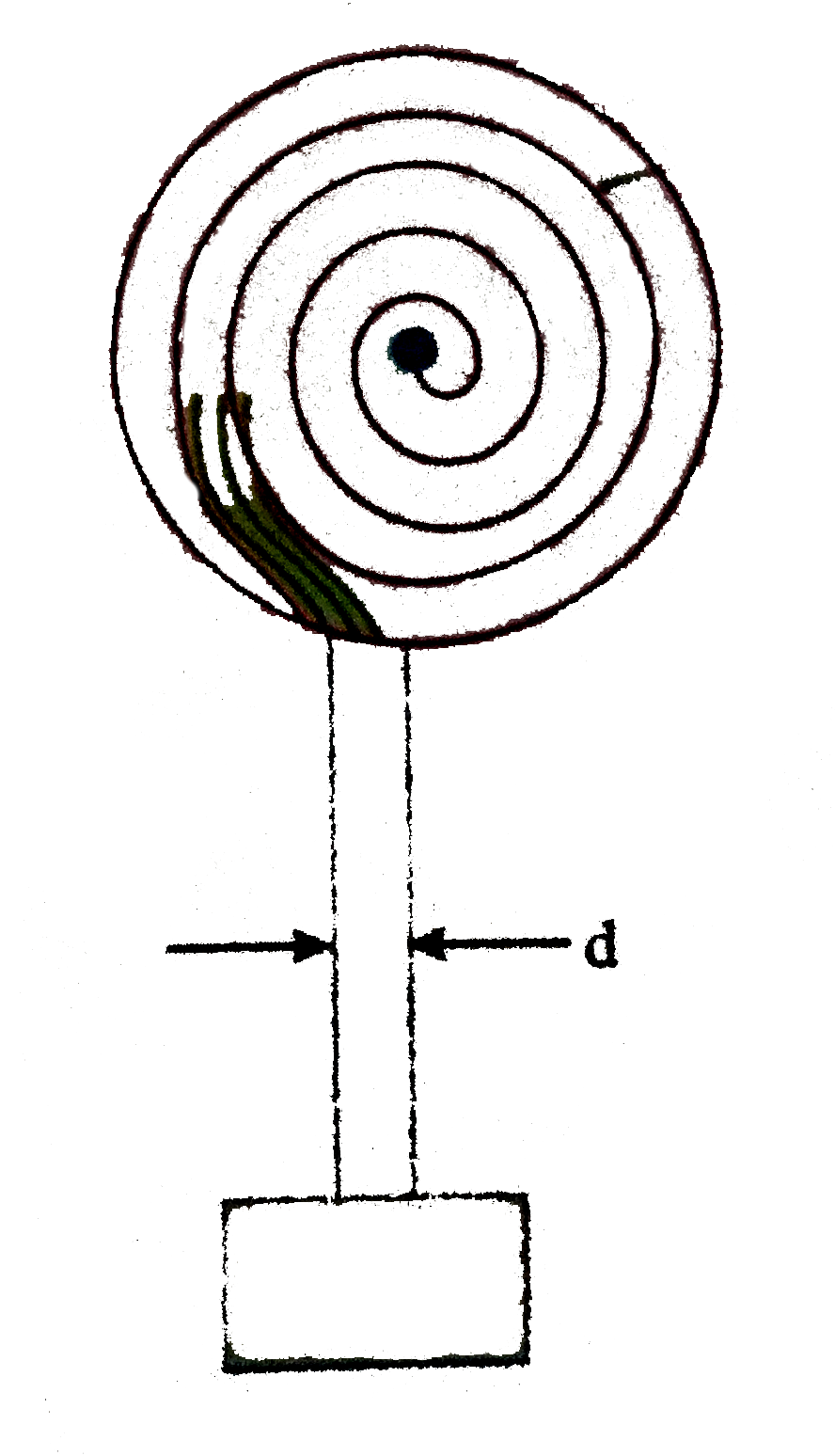
View SolutionIn the given figure, a smooth parabolic wire track lies in the `xy`-plane (vertical). The shape of track is defined by the equation `y=x^(2)`. A ring of mass `m` which can slide freely on the wire track, is placed at the position `A (1,1)`. The track is rotated with constant angular speed `omega` such that there is no relative slipping between the ring and the track. The value of `omega` is
View SolutionA disc of radius `R` has a light pole fixed perpendicular to the disc at its periphery whish in turn has a pendulum of legth `R` attached to its other end as shown in figure. The disc is rotated with a constant angular velocity `omega` The string is making an angle `45^(@)` with the rod. Then the angular velocity `omega` of disc is

View SolutionA particle travels along the arc of a circle of radius `r`. Its speed depends on the distance travelled `l` as `v=asqrtl` where 'a' is a constant. The angle `alpha` between the vectors of net acceleration and the velocity of the particle is
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of the acceleration are equal. If its speed at `t = 0` is `u_(0)` the time taken to complete the first revolution is :
View SolutionParticle `A` moves with `4m//s` along positive `y-`axis and particle `B` in a circle `x^(2)+y^(2)=4` (anticlockwise) with constant angular velocity `omega=2rad//s`. At time `t=0` particle is at `(2m,0)`. Then
View SolutionA particle 'A' moves along a circle with a velocity `v=at`, where `a=0.50m//s^(2)`. Another particle `B` moves along a diameter `OO'` of the circle with the velocity `v=at`. Both the particles start simultaneously at `t=0` from the point `O` on the circle. For these particles, (the radius of circle`=1m`).

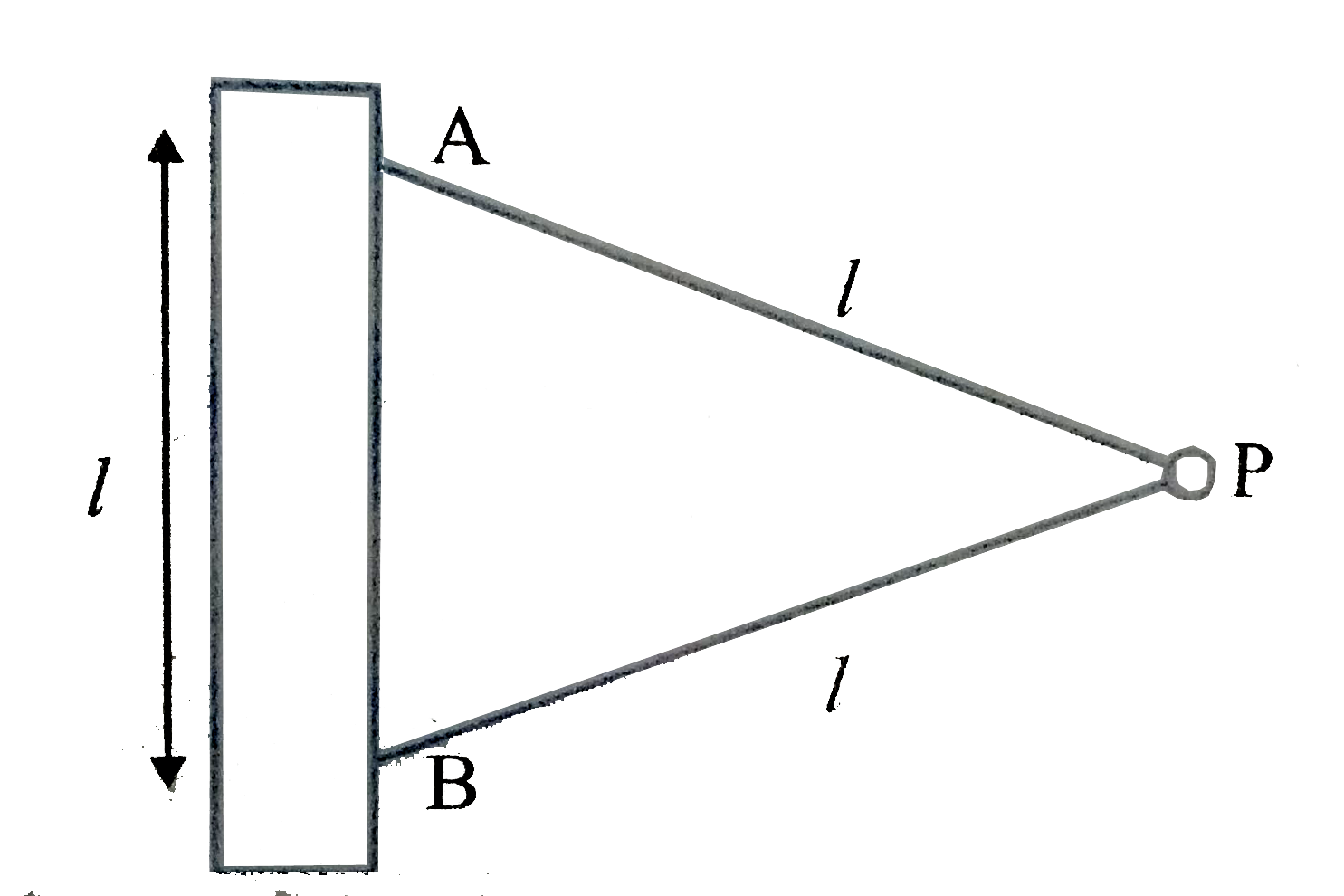
View SolutionA particle `P` of mass `m` is attached to a vertical axis by two strings `AP` and `BP` of legth `l` each. The separation `AB=l`, rotates around the axis with an angular velocity `omega`. The tension in the two string are `T_(1)` and `T_(2)`. Then
View SolutionA body moves on a horizontal circular road of radius `r`, with a tangential acceleration `a_(t)`. The coefficient of friction between the body and the road surface Is `mu`. It begins to slip when its speed is `v`.
(i) `v^(2)=murg`
(ii) `mug=(v^(4)/(r^92))+a_(t))`
(iii) `mu^(2)g^(2)=(v^(4)/(r^(2)+a_(t)^(2))`
(iv) The force of friction makes an angle `tan^(-1)(v^(2)//a_(t)r)` with the direction of motion at the point of slipping.
View Solution
LEVEL-VI questions and complete solutions for chapter CIRCULAR MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11