Complete Solutions to Level 3 Passage 2 of chapter GASEOUS STATE of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | GASEOUS STATE |
| NARENDRA AWASTHI | Level 3 Passage 2 |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
Collision cross-section is an area of an imaginary sphere of radius `sigma` around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
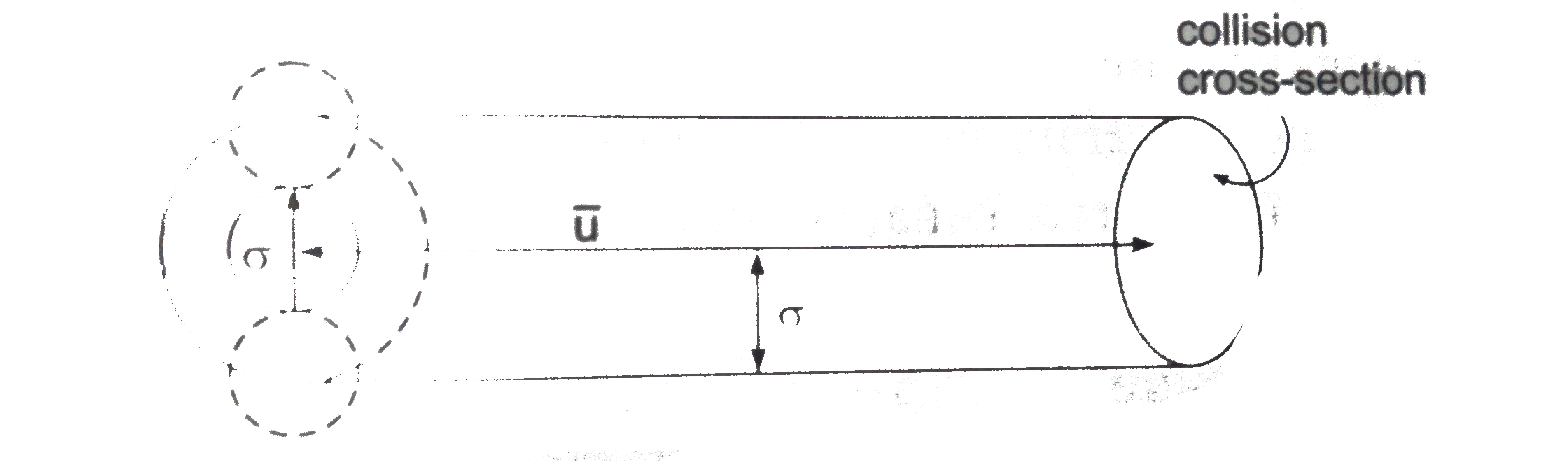
`V=(pisigma^(2))overline(u)` where `overline(u)` is the average speed
If `N^(**)` is the number of molecules per unit volume, then the number of molecules within the volume V is
`N=VN^(**)=(pisigma^(2)overline(u))N^(**)`
Hence, the number of collision made by a single molecule in unit time will be
`Z=N=(pi sigma^(2)overline(u))N^(**)`
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is `sqrt(2)overline(u)` as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
`Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(u)N^(**)`
The total number of bimolecular collisions `Z_(11)` per unit volume per unit time is given by
`Z_(11)=(1)/(2)(Z_(1)N^(**))"or" Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2)`
If the collsion involve two unlike molecules then the number of collisions `Z_(12)` per unit volume per unit time is given as
`Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2)`
where `N_(1)` and `N_(2)` are the number of molecules per unit volume of the two types of molecules, `sigma_(12)` is the average diameter of the two molecules and `mu` is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
`lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1))`
`"or "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**))`
For a given gas the mean free path at a particular pressure is :
View SolutionCollision cross-section is an area of an imaginary sphere of radius `sigma` around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
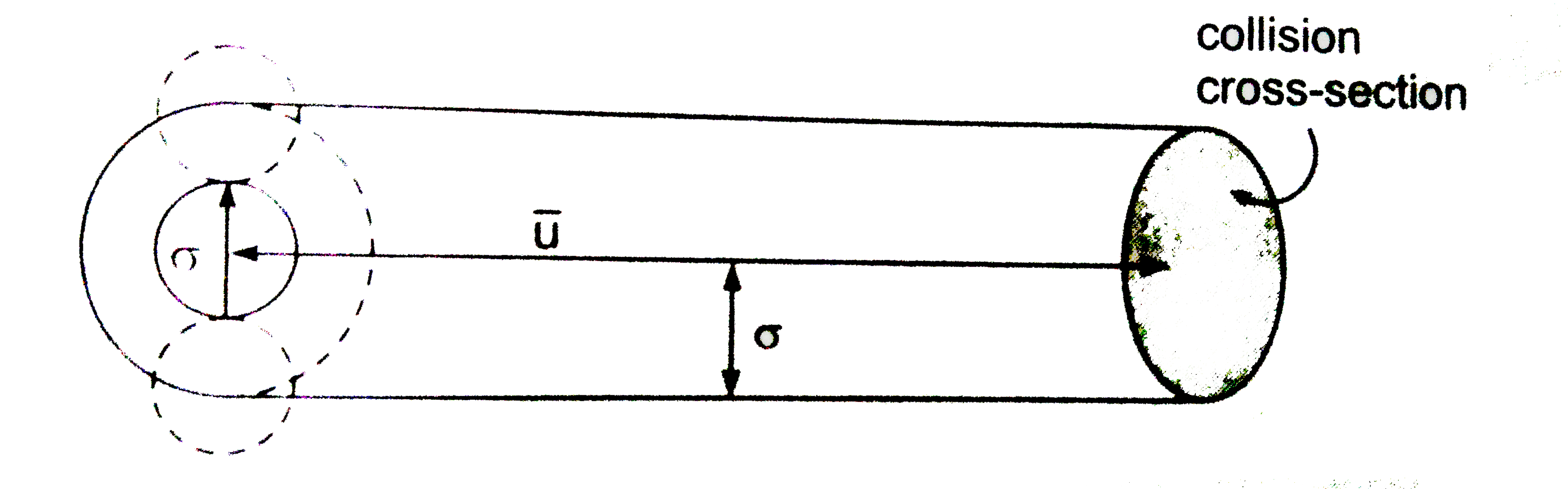
`V=(pisigma^(2))overline(u)` where `overline(u)` is the average speed
If `N^(**)` is the number of molecules per unit volume, then the number of molecules within the volume V is
`N=VN^(**)=(pisigma^(2)overline(u))N^(**)`
Hence, the number of collision made by a single molecule in unit time will be
`Z=N=(pi sigma^(2)overline(u))N^(**)`
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is `sqrt(2)overline(u)` as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
`Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(u)N^(**)`
The total number of bimolecular collisions `Z_(11)` per unit volume per unit time is given by
`Z_(11)=(1)/(2)(Z_(1)N^(**))"or" Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2)`
If the collsion involve two unlike molecules then the number of collisions `Z_(12)` per unit volume per unit time is given as
`Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2)`
where `N_(1)` and `N_(2)` are the number of molecules per unit volume of the two types of molecules, `sigma_(12)` is the average diameter of the two molecules and `mu` is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
`lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1))`
`"or "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**))`
Three ideal gas samples in separate equal volume containers are taken and following data is given :
`{:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):}`
Calculate ratio of collision frequencies `(Z_(11)) (A:B:C)` of following for the three gases.
View SolutionThree ideal gas samples in separate equal volume containers are taken and following data is given :
`{:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):}`
Calculate number of collision by one molecule per sec `(Z_(1))`.
(a)`4:1:4`
(b)`1:4:4`
(c)`4:3:2`
(d)`1:2:4`
View SolutionA monometer contains a liquid of density `5.44g//cm^(3)` is attached to a flask containing gas `A' as follows
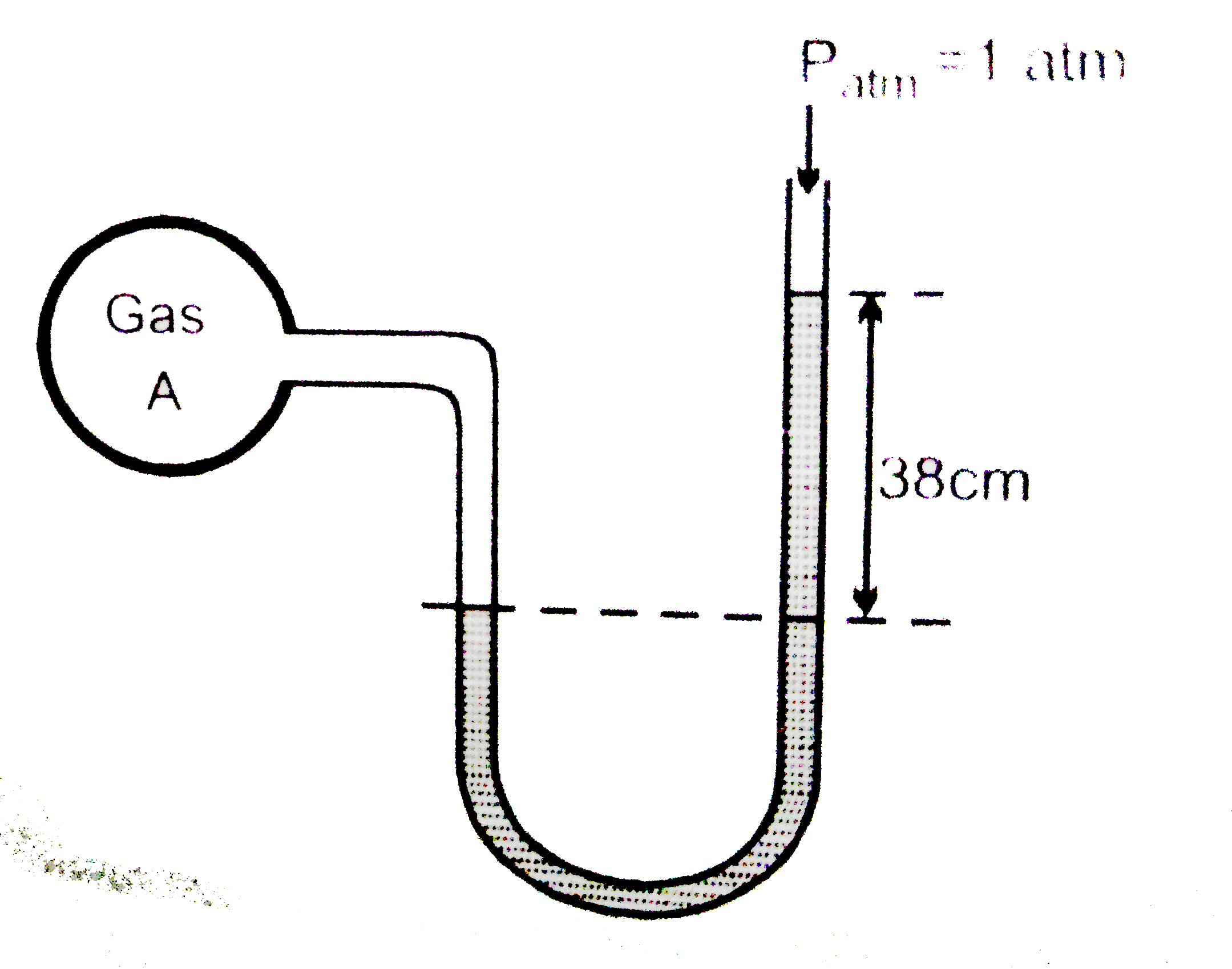
If the same liquid is used in barometer to measure the atmospheric pressure, then what will be the length of the liquid column, which exerts pressure equal to 1 atm ? (density of Hg = 13.6`g//cm^(3)`)
View SolutionThree ideal gas samples in separate equal volume containers are taken and following data is given :
`{:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):}`
Calculate number of collision by one molecule per sec `(Z_(1))`.
(a)`4:1:4`
(b)`1:4:4`
(c)`4:3:2`
(d)`1:2:4`
View SolutionA manometer contains a liquid of density `5.44g//cm^(3)` is attached to a flask containing gas 'A' as follows
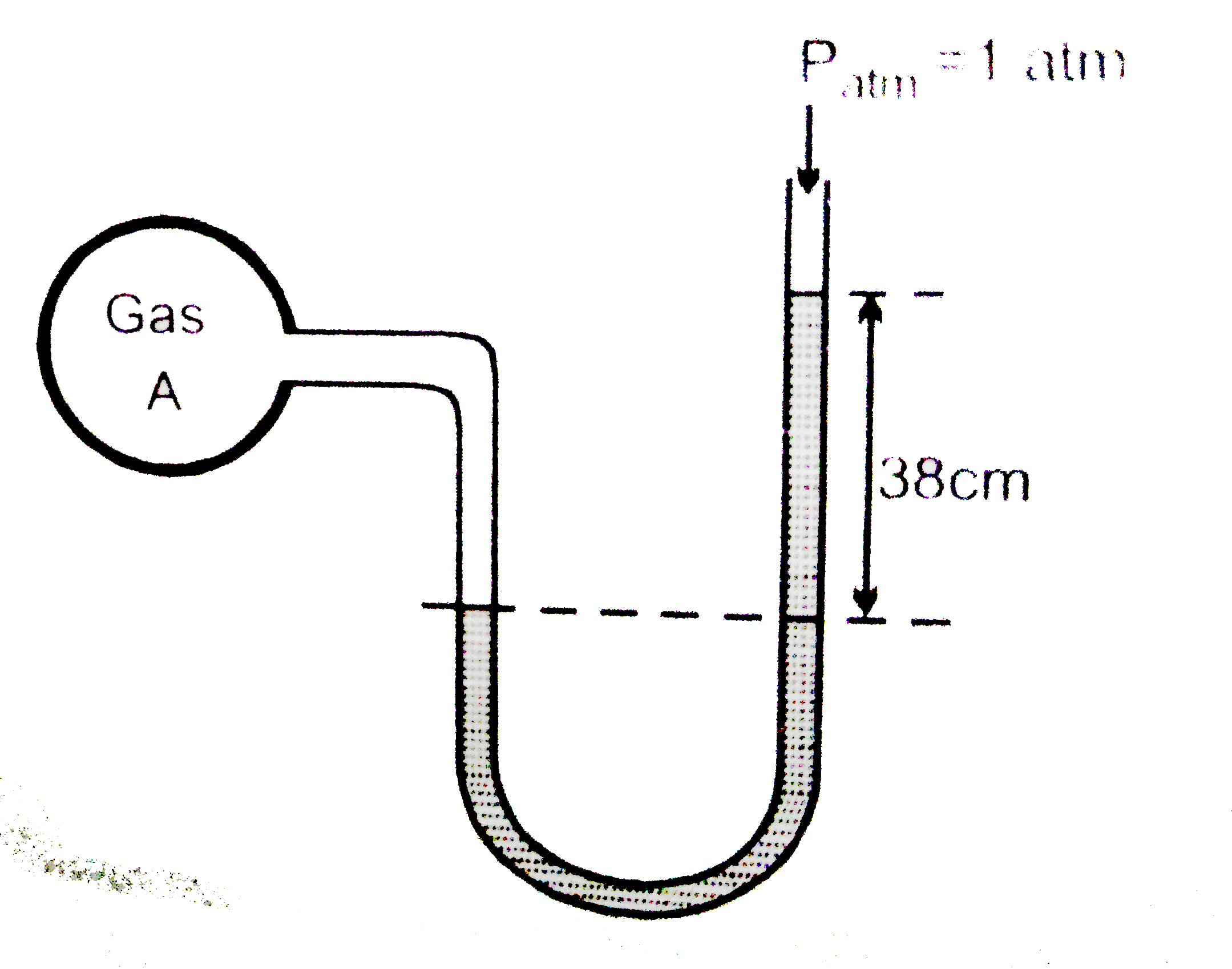
If the same liquid is used in barometer to measure the atmospheric pressure, then what will be the lengh of the liquid columnm which exerts pressure equal to 1 atm ? (density of `Hg=13.6g//cm^(3)`)
View Solution
Level 3 Passage 2 questions and complete solutions for chapter GASEOUS STATE of NARENDER AVASTHI CHEMISTRY (ENGLISH) of Class 11