Complete Solutions to Level 2 of chapter GASEOUS STATE of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | GASEOUS STATE |
| NARENDRA AWASTHI | Level 2 |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
Consider the composite system, which is held at 300 k , shown in the following figure. Assuming ideal gas behavior, calculate the total pressure if the barriers sparating the compartments are removed. Assume that the volume of the barriers is negligible. (Given : R =0.082 atm L/mol. K)

View Solution11 moles of `N_(2)` and 12 moles of `H_(2)` mixture reacted in 2.0 litre vessel at 800 K. After equilibrium was reached, 6 mole of `H_(2)` was present. 3.58 litre of liquid water is injected in equibrium mixture and resultant gaseous mixture suddenly cooled to 300K. What is the final pressure of gaseous mixture? Neglect vapour pressure of liquid solution. Assume (i) all `NH_(3)` dissolved in water (ii) no change in volume of liquid (iii) At 300 K no reaction takes place between `N_(2)` and `H_(2)`
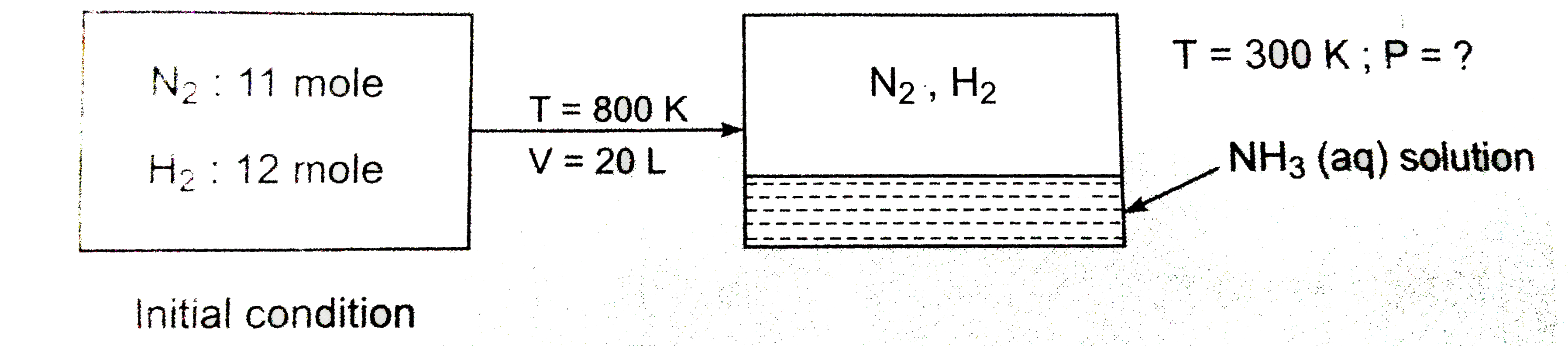
(a)18.47 atm
(b)60 atm
(c)22.5 atm
(d)45 atm
View SolutionTwo vessels connected by a valve of negligible volume. One container (I) has 2.8 g of `N_(2)` at temperature `T_(1) (K)`. The other container (II) is completely evacuated. The container (I) is heated to `T_(2)(K)`while container (II) is maintained at `T_(2)//3(K)`. volume of vessel (I) is half that of vessel (II). If the valve is opened then what is the mass ratio of `N_(2)` is both vessel `(W_(I)//W_(II))`?
View SolutionA mixture of `NH_(3(g))` and `N_(2)H_(4_((g)))` is placed in a sealed container at `300 K`. The total pressure is `0.5 atm`. The container is heated to `1200 K`, at which time both substances decompose completely according to the equations:
`2NH_(3(g))rarrN_(2(g))+3H_(2(g))`
`N_(2)H_(4_((g)))rarrN_(2(g))+2H_(2(g))`
After decomposition is complete, the total pressure at `1200 K` is found to be `4.5 atm`. Find the amount (mole) per cent of `N_(2)H_(4(g))` in the original mixture.
View SolutionCorrect expression for density of an ideal gas mixture of two gases 1 and 2, where `m_(1)` and `m_(2)` are masses and `n_(1)` and `n_(2)` are moles and `M_(1)` and `M_(2)` are molar masses.
View SolutionTwo closed vessels of equal volume containing air at pressure `P_(1)` and temperature `T_(1)` are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at `T_(1)` and that in the other at `T_(2)`, what will be the pressure in the vessels?
View SolutionA balloon containing 1 mole air at 1 atm initially is filled further with air till pressure increases to 4 atm. The intial diameter of the ballon is 1 m and the pressure at each stage is proportional to diameter of the balloon. How many moles of air added to change the pressure from 1 atm to 4 atm.
View SolutionIf Pd vs. P(where P denotes pressure in atm and d denotes density in gm/L ) is plotted for He gas (assume ideal ) at a particular temperature. If `[(d)/(dP)(pd)]_(P=8.21"atm")=5,` then the temperature wil be
View SolutionWhat is the density of wet air with 75% relative humidity at 1 atm and 300 K? Given : vapour pressure of `H_(2)O` is 30 torr and average molar mass of air is 29 g `mol^(_1)` .
View Solution7 moles of a tetra-atomic non-linear gas 'A' at 10 atm and T K are mixed with 6 moles of another gas B at `(T)/(3)K` and 5 atm in a closed, rigid vessel without energy transfer with surroundings. If final temperature of mixture was `(5T)/(6) K,` then gas B is ? (Assuming all modes of energy are active)
View SolutionThree closed rigid vessels, A, B and C, which initially contain three different gases at different temperatures are connected by tube of negligible volume, without any energy transfer with surroundings. The vessel A contain 2 mole Ne gas, at 300 K, vessel 'B' contain 2 mole `SO_(2)` gas at 400 K and vessel 'C' contain 3 mole `CO_(2)` gas at temperature 500 K. What is the final pressure (in atm) attained by gases when all valves of connecting three vessels are opened and additional 15.6 kcal hear supplied to vessels through valve. The volume of A, B and C vessel is 2, 2 and 3 litre respectively
Given :R =2 calorie/mol-K,`C_(v)(Ne)=3//2R,C_(v)(CO)=5//2R and C_(v)(SO_(2))=3R`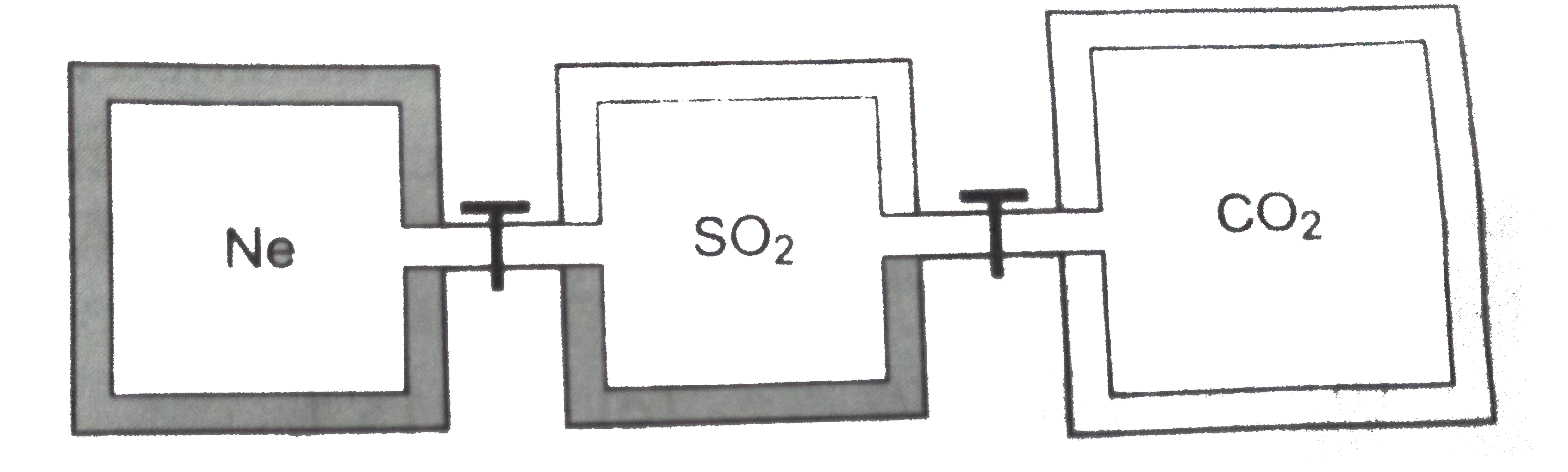
View SolutionGas molecules each of mass `10^(-26)` kg are taken in a container of volume `1 dm^(3)` . The root mean square speed of gas molecules is 1 km `sec^(-1)` .What is the temperature fo gas molecules.
(Given : `N_(A) =6xx10^(23),R=8J//mol.K`)
View SolutionA balloon of diameter 21 meter weight 100 kg. Calculate its pay-load, if it is filled with He at 1.0 atm and `27^(@)C`. Density of air is 1.2 kg `m^(-3)` . (Given : R=0.082 L atm `K^(-1)mol^(-1)`)
View SolutionA given volume of ozonised oxygen (containing 60% oxygen by volume ) required 220 sec to effuse while an equal volume of oxygen took 200 sec only under identical conditions. If density of `O_(2)` is 1.6 g/L then find density of `O_(3)`.
View SolutionIf 250 mL of `N_(2)` over water at `30^(@)C` and a total pressure of 740 torr is mixed with 300 mL of Ne over water at `25^(@)C` and a total pressure of 780 torr, what will be the total pressure if the mixture is in a 500 mL vessel over water at `35^(@)C`.
(Given : Vapour pressure (Aqueous tension )of `H_(2)O` at `25^(@)C`, `30^(@)C` and `35^(@)C` are 23.8, 31.8 and 42.2 torr respectively. Assume volume of `H_(2)O(l)` is negligible in final vessel)
View SolutionA bulb of constant volume is attached to a manometer tube open at other end as shown in figure. The manometer is filled with a liquid of density `(1//3)^("rd")` that of mercury. Initially h was 228 cm.
Through a small hole in the bulb gas leaked assuming pressure decreases as `(dP)/(dt)=-kp.`If value of h is 114 cm after 14 minutes, what is the value of k (in `"hour"^(-1)`)?
[ Use : In (4/3) =0.28 and density of Hg =13.6 g/mL.].
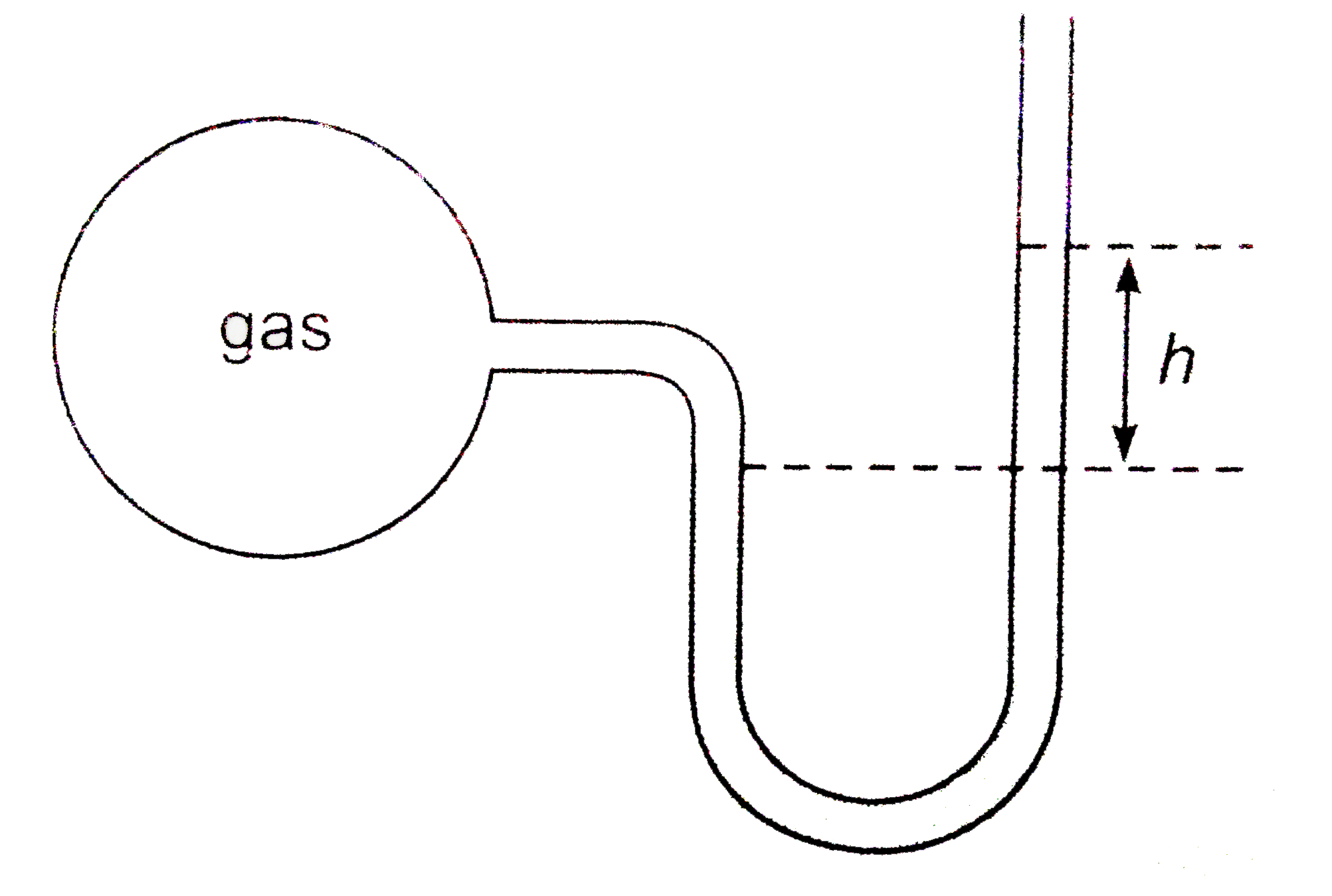
View SolutionA mixture of nitrogen and water vapours is admitted to a flask at 760 torr which contains a sufficient solid drying agent. After long time the pressure attained a steady value of 722 torr.
If the experiment is done at `27^(@)C` and drying agent increase in mass by 0.9 gm, what is the volume of the flask? Neglect any possible vapour pressure of drying agent and volume occupied by drying agent.
View SolutionAt room temperature following traction goes to completion
`2AB(g)+B_(2)(g)rarr2AB_(2)(s)`
`AB_(2)` is solid with negligble vapour pressure below `0^(@)C`. At 300 K, the AB in the smaller flask exerts a pressure of 3 atm and in the larger flask `B_(2)` exerts a pressure of 1 atm at 400 K when they are separated out by a close valve, The gases are mixed by opening the stop cock and after the end of the reaction the flask are cooled to 250 K

The final pressure is :
View SolutionA vessel of uniform cross-section of length 500 cm as shown in figure is divided in two parts by a weightless and frictionless piston one part contains 5 moles of He(g) and other part 2 moles of `H_(2)(g)` and 4 moles of `O_(2)(g)` added at the same temperature and pressure in which reaction takes place finally vessel cooled to 300 K and 1 atm. What is the length of He compartment?
(Assume volume of piston and vol. of `H_(2)O(l)` formed are negligible)
View SolutionFor a real gas (mol.mass =60) if density at critical point is `0.80g//cm^(-3)` and its `T_(c)=(4xx10^(5))/(821)K,` then van der Waals' constant a ( in atm `L^(2)mol^(-2)`) is
View SolutionThe van der Waals' constant 'b' of a gas is `4pixx 10^(-4)L//mol.` How near can the centeres of the two molecules approach each other? [Use :`N_(A)=6xx10^(23)`]
View SolutionThe density of vapour of a substance `(X)` at 1 atm pressure and 500 K is `0.8 kg//m^(3)`. The vapour effuse through a small hole at a rate of `4//5` times slower than oxygen under the same condition. What is the compressibility factor `(z)` of the vapour ?
View Solutionvan der Waal's gas equation can be reduced to virial eqation and virial equation (in terms of volume) is`Z=A+(B)/(V_(m))+(C)/(V_(m)^(2))+……..`
where A =first virial coefficient, B=second virial coefficient ,C = third virial coefficient. The third virial coeffdient of Hg(g) is 625 `(cm^(2)//"mol")^(2)`. What volume is available for movement of 10 moles He(g) atoms present in 50 L vessel?
View SolutionIf the slope of 'Z' (compressibility factor) vs. 'p' curve is constant `("slope"=(pi)/(492.6)atm^(-1))` at a particular temperature (300 K) abd very high pressure, then calculate diameter of the molecules.
(Given : `N_(A)=6.0xx10^(23), R=0.0821 atm.Lmol^(-1)K^(-1)`)
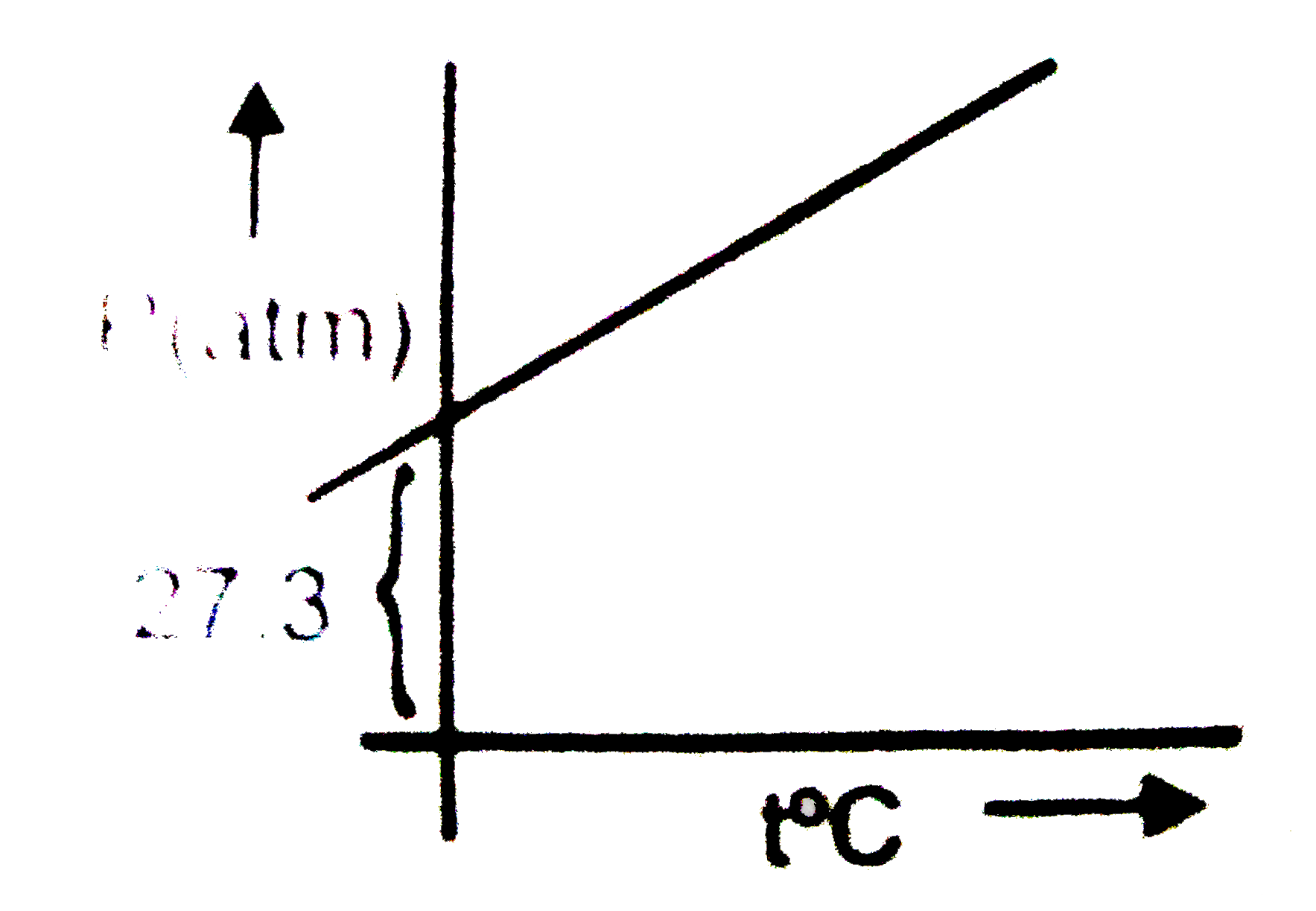
View SolutionA graph is plotted between p (atm) vs `t^(@)C` for 10 mol of an ideal gas as follows:
Then slope of curve and volume of container (L) respectively, are:
View SolutionFor two samples of ideal gases A and B curves are plotted n vs V (volume of container ) at 16.42 atm pressure. Then temperature of A and B respectively are:
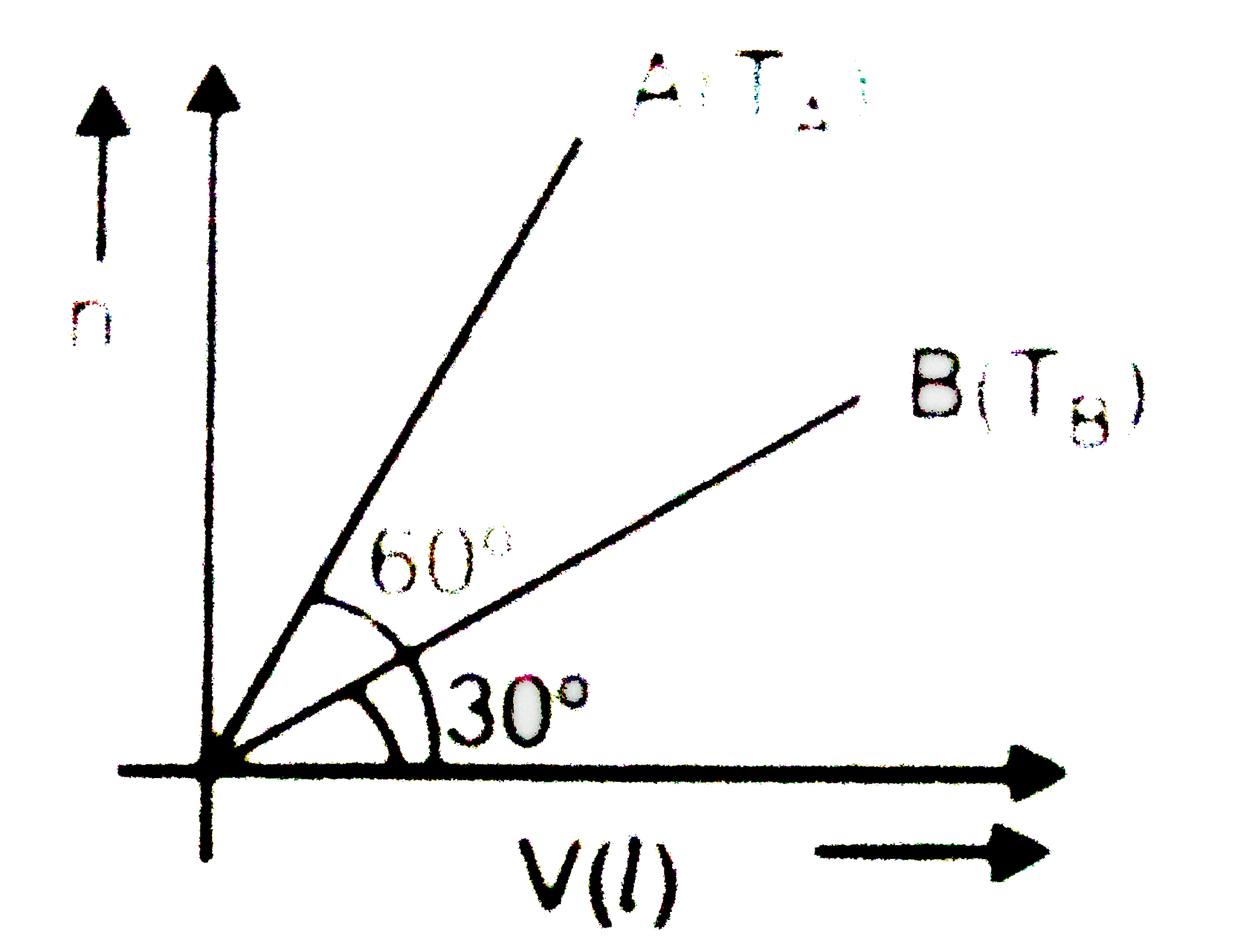
(a)`(200)/(sqrt(3))K,200sqrt(3) K`
(b)`(200)/(sqrt(3))@_(C),(200sqrt(3))^(@)C`
(c)`200sqrt(3)K,(200)/(sqrt(3))K`
(d)`200K,(sqrt(3))/(200)K`
View SolutionAt a constant temperature what should be the percentage increase in pressure for a `10%` decrease in the volume of gas ?
(a)`11%`
(b)`20%`
(c)`5%`
(d)`50%`
View Solution6 litre `H_(2)O` is placed in a closed evacuated room of volume 8.27 litre at the temperature 300K. The density of liquid water at 300 K is 1.0 gm/ml. the vapour pressure of water at 300 K is 22.8 mm Hg. Neglect the change in volume of liquid water by vaporization. `{:("List I",,"List II"),("(P) Mass of watwer vapour formed (in gm)",,"(1) 6"),("(Q) Moles of water vapour fomed",,"(2) 18"),("(R) Approx. mass of liquid water left (in kg)",,"(3) 3"),("(S) Total moles of atoms in vapour form",,"(4) 1"):}`
View SolutionMatch the items of colums I and II.

View SolutionMatch the following columns
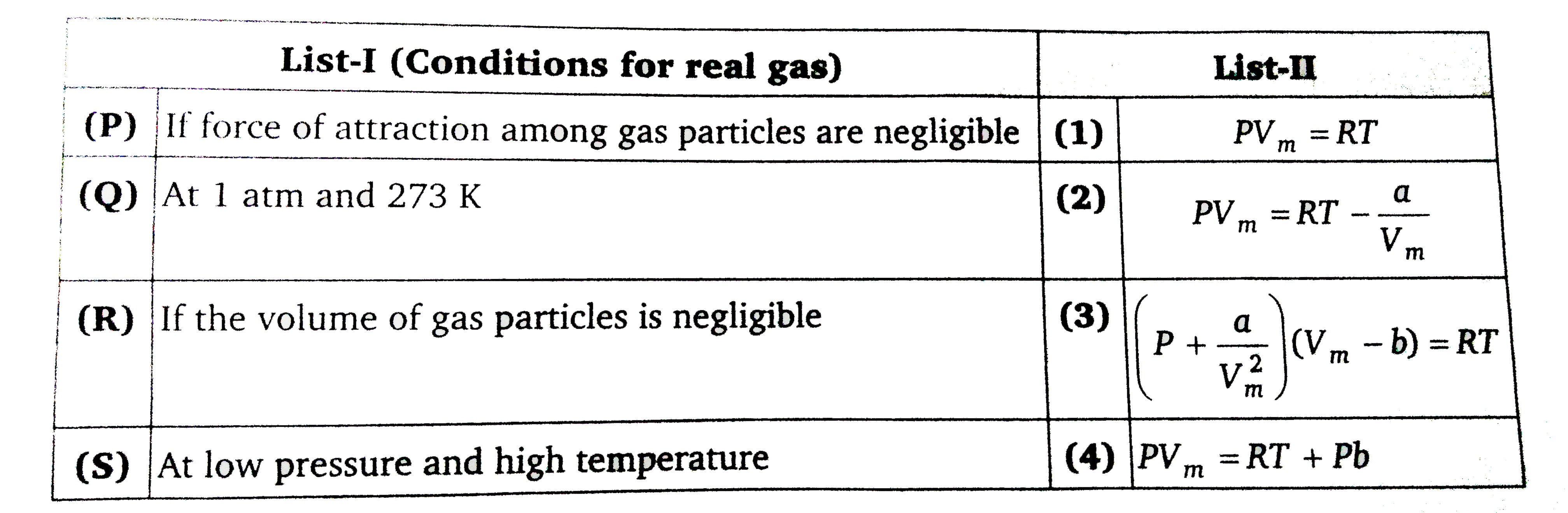
View Solution
Level 2 questions and complete solutions for chapter GASEOUS STATE of NARENDER AVASTHI CHEMISTRY (ENGLISH) of Class 11