Complete Solutions to बहुविकल्पीय प्रश्न of chapter कणों के निकाय की गति और घुर्णो गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | कणों के निकाय की गति और घुर्णो गति |
| NAVBODH PARIKSHA SAAR | बहुविकल्पीय प्रश्न |
| Number Of Questions | 84 |
| Academic Year | 2023-24 |
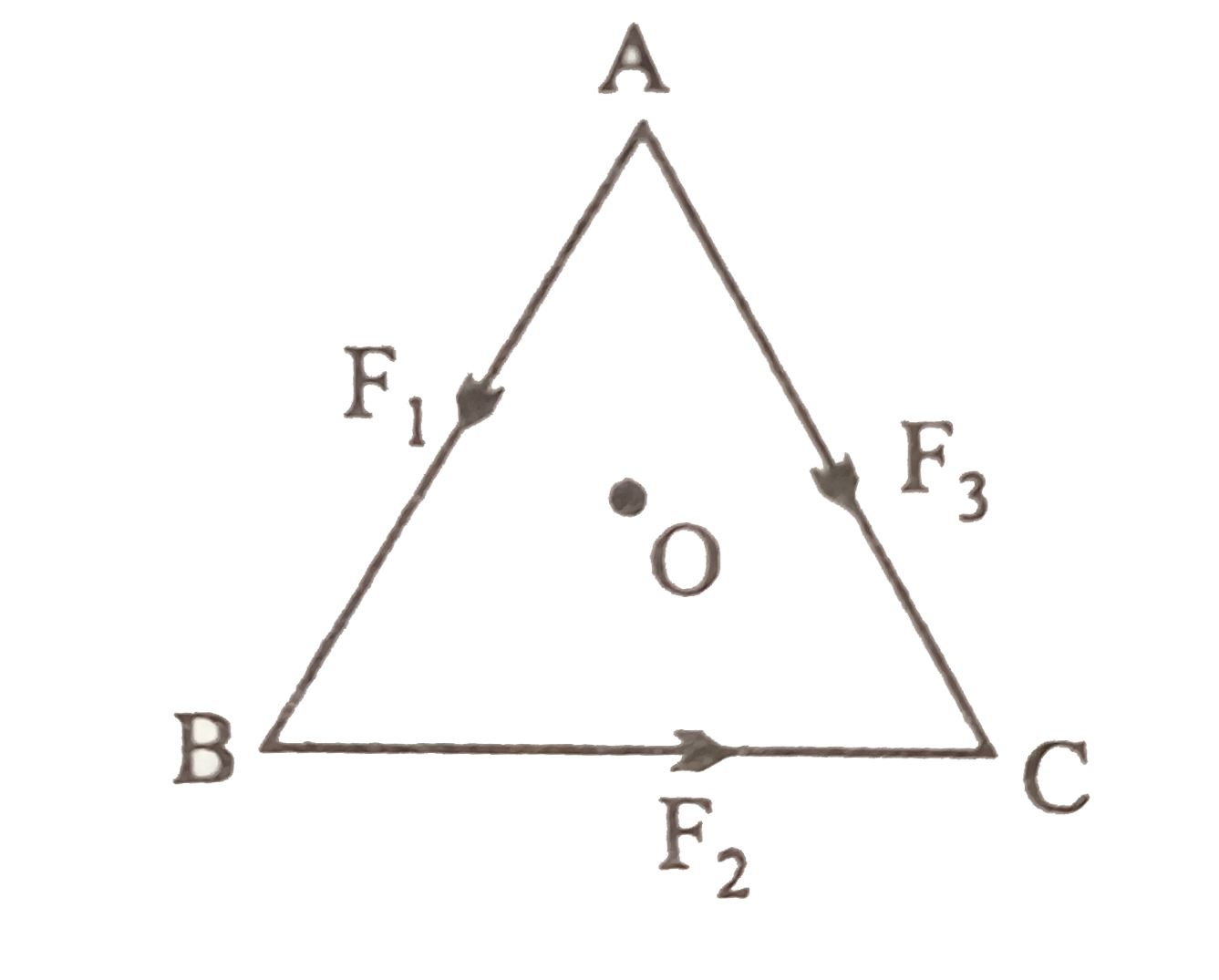
एक समबाहु त्रिभुज ABC का केंद्र O है । `F_(1),F_(2)` और `F_(3)` क्रमशः AB, BC व AC के अनुदिश कार्यरत बल हैं । `F_(3)` का मान क्या होगा जबकि O के परितः कुल बल - आघूर्ण शून्य है ।
View Solutionधातु के तीन गोले ( प्रत्येक की त्रिज्या r ) एक क्षैतिज तल पर एक - दूसरे से सटाकर इस प्रकार रखे गए हैं की उनके केंद्रों को मिलाने पर एक समबाहु त्रिभुज प्राप्त होता है निकाय का द्रव्यमान - केंद्र होगा -
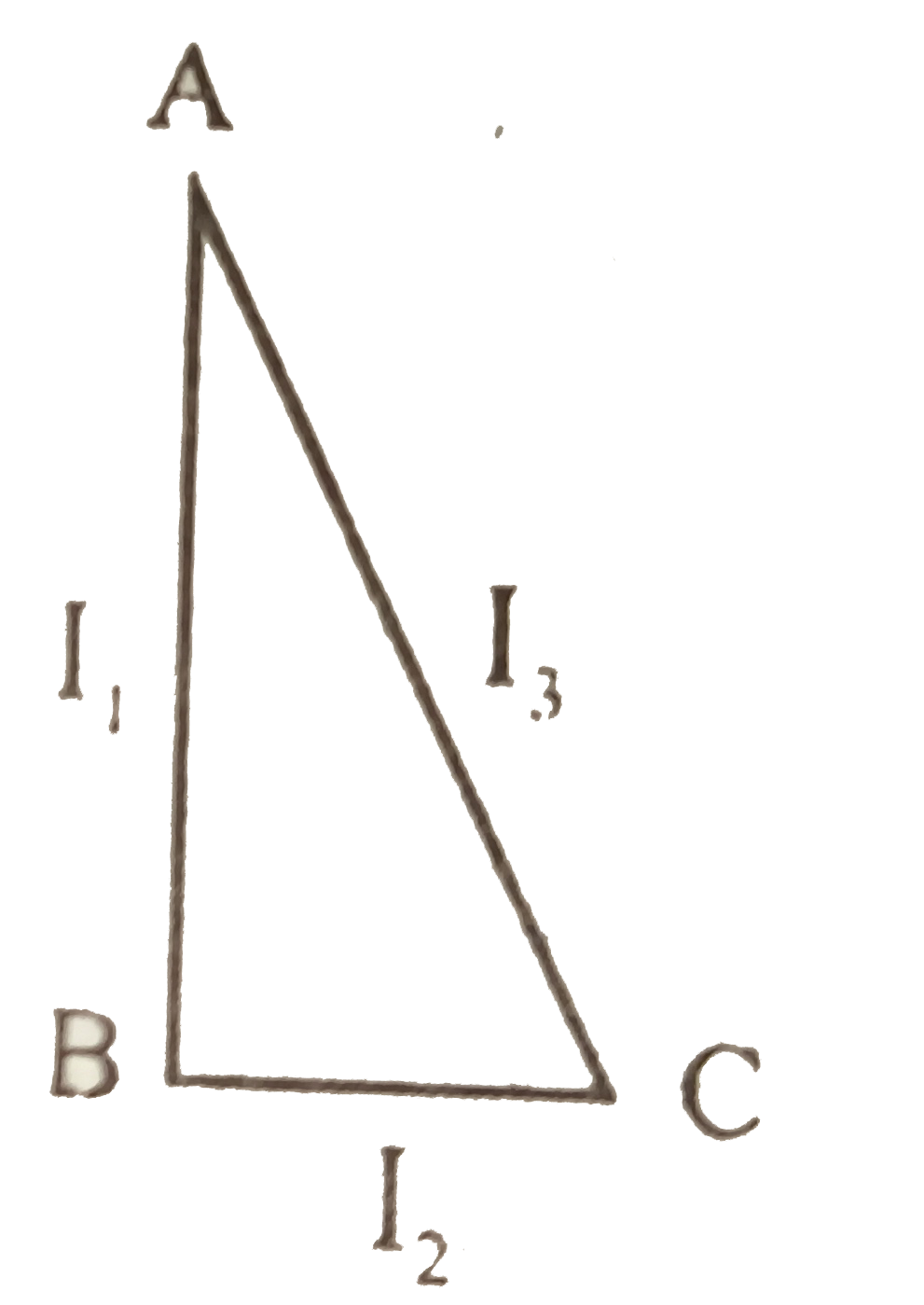
View SolutionABC एकसमान मोटाई की समकोणिक त्रिभुजाकार प्लेट है । इसकी भुजाएँ इस प्रकार हैं की `AB gt BC.` । यदि `I_(1), I_(2)` तथा `I_(3)` भुजाओं AB, BC तथा AC के परितः जड़त्व - आघूर्ण हों तो निम्न में से कौन - सा संबंध सही है
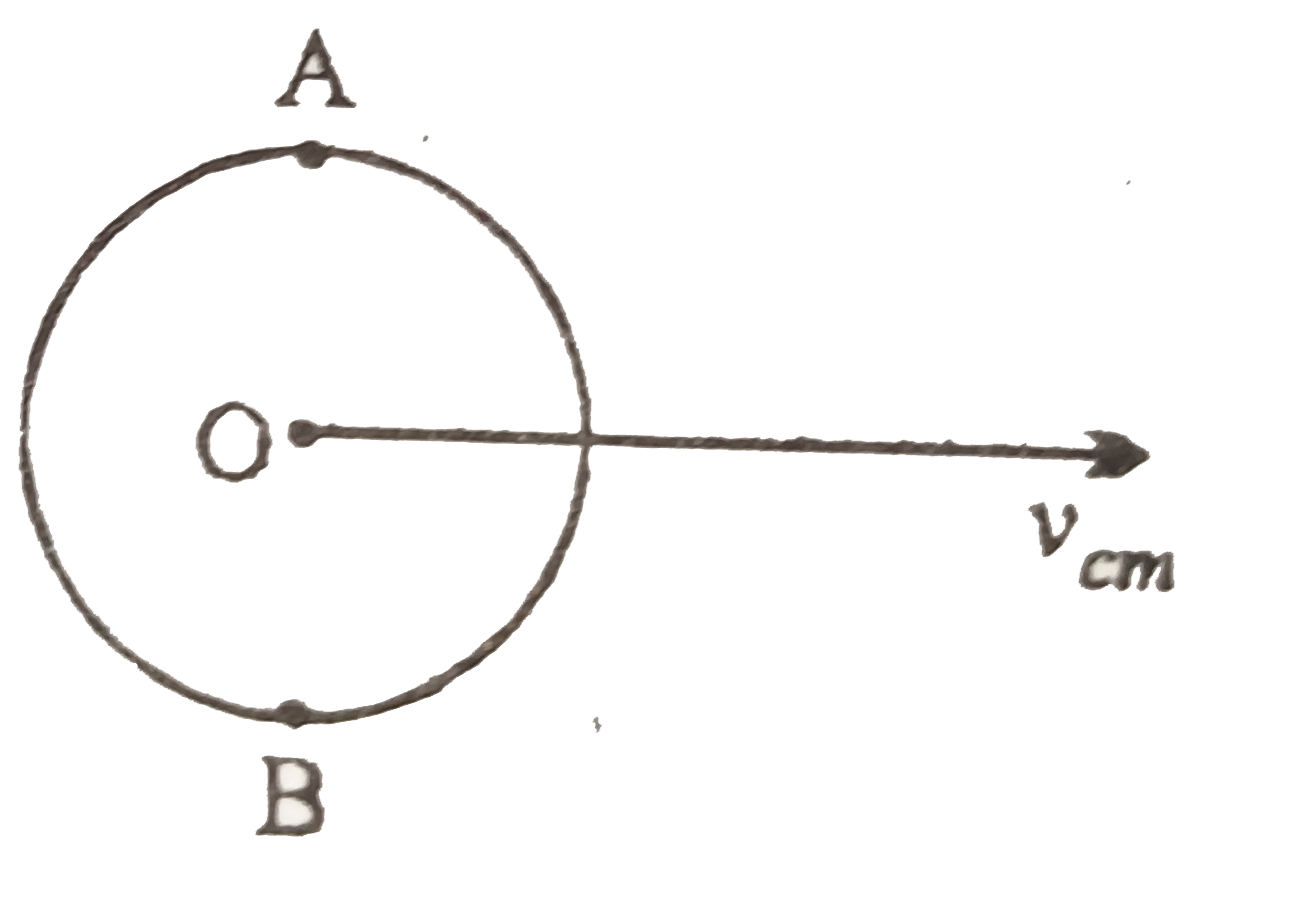
View Solutionसाइकिल का एक पहिया एक क्षैतिज तल पर बिना फिसले लुढ़क रहा है । द्रव्यमान केंद्र का वेग `v_(cm)` है । तब सत्य कथन होगा -
View Solutionएक चकती `omega` कोणीय वेग से घूम रही है। इस पर बच्चा बैठ जाता है । इस प्रक्रिया में क्या संरक्षित रहता है ।
View Solutionलोहे और एल्युमिनियम को प्रयोग करके एक वृत्ताकार चकती बनायी जाती है । इसके ज्यामितीय अक्ष के परितः जड़त्व आघूर्ण के अधिकतम होने के लिए इसे इस प्रकार बनाना चाहिए ताकि -
View Solutionएक क्षैतिज तल पर R त्रिज्या का एक ठोस गोला रखा है । निम्नतम बिंदु से h ऊँचाई पर गोले पर एक क्षैतिज बल F लगाया जाता है । द्रव्यमान - केंद्र के अधिकतम त्वरण के लिए -
View Solutionएक छड़ की लम्बाई 3 मीटर है तथा इसकी प्रति मीटर लम्बाई का द्रव्यमान एक सिरे से दूरी के अनुक्रमानुपाती है । इसी सिरे से छड़ के गुरुत्व केंद्र की दूरी होगी -
View Solutionद्रव्यमान M व त्रिज्या r की एक पतली रिंग अपने अक्ष के परितः नियत कोणीय वेग `omega` से घूम रही है । द्रव्यमान m के चार कण धीरे से इसके लंबवत दो व्यासों के सिरों पर रख दिए जाते हैं, तब रिंग का कोणीय वेग होगा
View Solutionएक गेंद बिना फिसले लुढ़कती है । द्रव्यमान - केंद्र से गुजरने वाली अक्ष के परितः इसकी घूर्णन त्रिज्या K है । यदि गेंद की त्रिज्या r हो तो इसकी कुल ऊर्जा का कितना भाग घूर्णन ऊर्जा है -
View SolutionM द्रव्यमान व R त्रिज्या का एक बेलन L लम्बाई व h ऊँचाई के आनत तल पर बिना फिसले लुढ़कता है । बेलन के द्रव्यमान केंद्र की चाल क्या होगी जब यह आनत तल की तली पर पहुँचता है।
View Solutionएक वृत्ताकार चकती, जिसका जड़त्व - आघूर्ण इसके तल के लंबवत तथा इसके द्रव्यमान - केंद्र से गुजरने वाले अक्ष के परितः `I_(2)` है, को समान अक्ष के परितः `omega` कोणीय वेग से घूर्णन करने वाली तथा जड़त्व - आघूर्ण `I_(1)` वाली एक दूसरी चकती के ऊपर रखा जाता है । चकतियों के संयोग का अंतिम कोणीय वेग है
View Solutionएक पहिया जिसका अपने ऊर्ध्वाधर अक्ष के परितः जड़त्व आघूर्ण `2` किग्रा - मीटर`""^(2)` है, उसी अक्ष के परितः 60 घूर्णन - प्रति मिनट की दर से घूमता है । एक मिनट में पहिया का घूर्णन रोकने वाले बल - आघूर्ण का मान होगा।
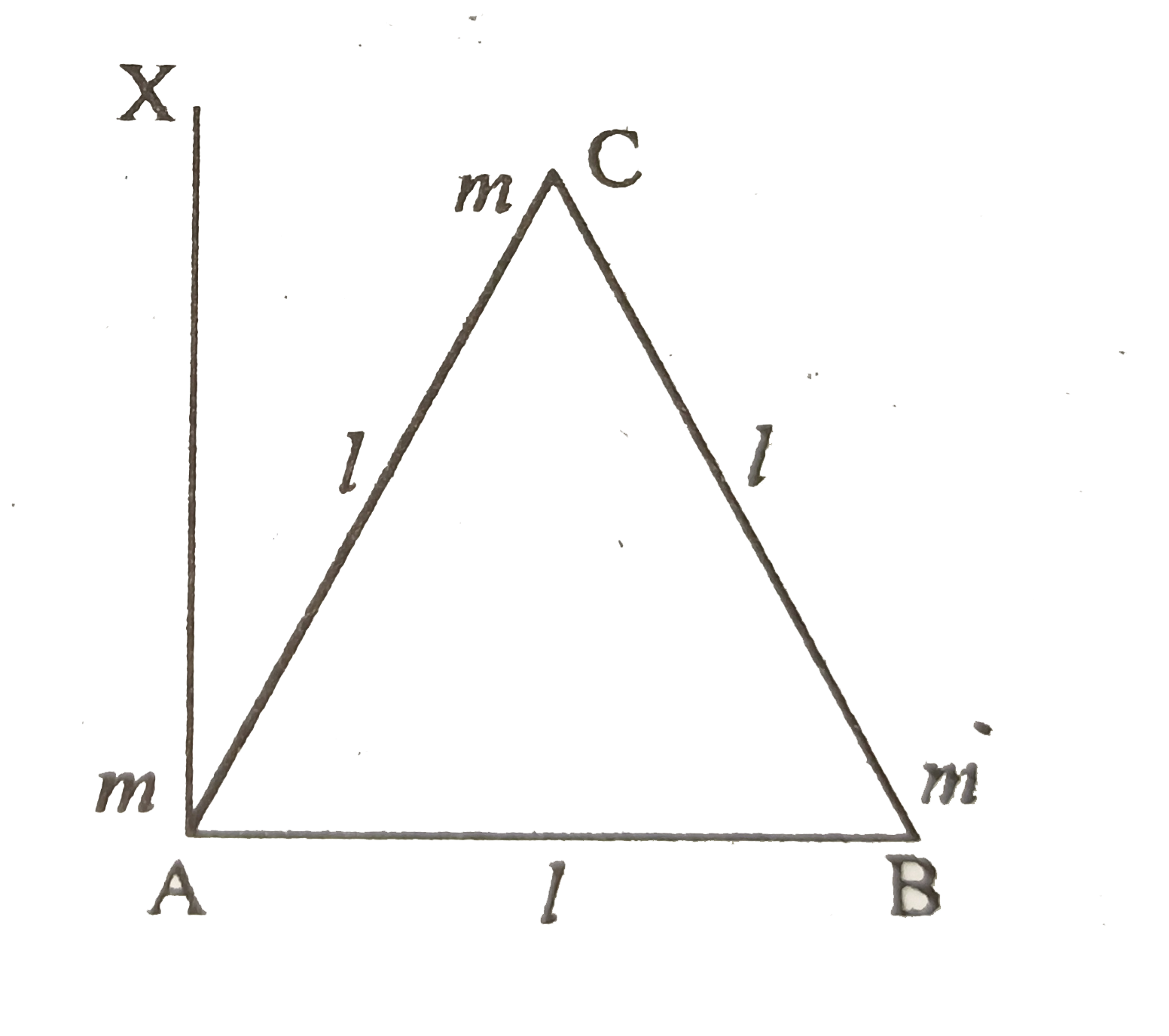
View Solutionm द्रव्यमान के तीन कण l सेमी भुजा के समबाहु त्रिभुज के शीर्षों पर स्थित हैं । त्रिभुज ABC के तल में AB के लंबवत रेखा AX के परितः निकाय का जड़त्व - आघूर्ण ग्राम सेमी होगा -
View Solutionत्रिज्या R और द्रव्यमान M का एक ड्रम `theta` कोण पर आनत एक तल पर बिना फिसले लुढ़कता है । घर्षण बल -
View Solutionएकसमान वृत्तीय चकती की त्रिज्या R तथा द्रव्यमान M है । इस चकती के व्यास के सिरे पर चकती को छूती हुई चकती के तल के लंबवत अक्ष के परितः चकती का जड़त्व - आघूर्ण
View SolutionL लम्बाई की एक नली को एक असंपीड्य द्रव से पूरा भरकर इसे दोनों सिरों से बंद कर दिया गया है । बंद द्रव का द्रव्यमान M है । इस नली को एक क्षैतिज तल में नली के एक सिरे के परितः अचर कोणीय वेग `omega` से घुमाया जाता है । द्रव द्वारा नली के दूसरे सिरे पर क्रियाकारी बल होगा -
View Solutionएक अचर दंड की लम्बाई `l` तथा द्रव्यमान m है । यह ऊर्ध्व तल में A के सापेक्ष घूर्णन करने को स्वतन्त्र है । दंड को क्षैतिज प्रारंभिक स्थिति में विमुक्त किया जाता है । दंड का प्रारंभिक कोणीय त्वरण होगा ।
(A के सापेक्ष दंड का जड़त्व - आघूर्ण =`(ml^2)/(3)` है ) ।

View Solutionएक चक्र का कोणीय त्वरण 3.0 रेडियन / सेकंड`"^(2)` तथा प्रारंभिक कोणीय चाल 2.0 रेडियन / सेकंड है । 2 सेकंड के काल में इसके घुमावों का रेडियन मान होगा -
View Solutionएक वृत्तीय चकती और वृत्तीय रिंग, जिनके द्रव्यमान और त्रिज्या समान हैं, के अपने- अपने अक्ष के परितः परिभ्रमण त्रिज्याओं का अनुपात होगा -
View Solutionलम्बाई L और द्रव्यमान M की एक पतली छड़ को अपने मध्य बिंदु पर `90^(@)` के कोण पर मोड़ा गया है । मुड़ी छड़ के दोनों भागों से बने तल के लम्बवत एवं मोड़ से गुजरने वाली अक्ष के परितः मुड़ी छड़ का जड़त्व - आघूर्ण होगा -
View Solutionयदि वलय व चकती के कोणीय संवेग बराबर हैं तो उनकी घूर्णन गतिज ऊर्जाओं का अनुपात होगा -
View Solutionयदि 2l लम्बाई की छड़ की प्रति इकाई लम्बाई का द्रव्यमान m है तो छड़ के केंद्र पर जड़त्व-आघूर्ण होगा -
View Solution8kg एवं 4kg के दो द्रव्यमान किसी 1 मीटर लंबी भारहीन छड़ के सिरे पर लटके है तो छड़ के केंद्र से जाने वाले लंबवत अक्ष के परितः निकाय का जड़त्व - आघूर्ण होगा -
View Solutionसमान द्रव्यमान का एक ठोस गोला, खोखला गोला तथा एक वलय को एक घर्षण रहित आनत तल में छोड़ा जाता है । ये सभी नीचे की ओर फिसलते हैं । किसका त्वरण अधिकतम होगा -
View Solutionएक वृत्ताकार चकती X जिसकी त्रिज्या R है, t मोटाई की लोहे की प्लेट से बनी है । 4R त्रिज्या की दूसरी चकती `Y,(t)/(4)` मोटाई की लोहे की प्लेट से बनी है । दोनों चकतियों के जड़त्व - आघूर्णों `I_(x)` और `I_(y)`, में संबंध होगा
View Solutionएकसमान वृत्तीय गति करते हुए एक कण का कोणीय संवेग L है । यदि इसकी कोणीय आवृत्ति दुगनी तथा गतिज ऊर्जा आधी कर दी जाए तो नया कोणीय संवेग होगा ।
View Solutionएक ठोस गोला A तथा एक अन्य खोखला गोला B समान द्रव्यमान तथा समान बाहरी त्रिज्या के हैं इन गोलों के अपने व्यासों के परितः जड़त्व- आघूर्ण `I_(A)` और `I_(B)` इस प्रकार हैं कि
View SolutionM द्रव्यमान का कोई पिंड A गुरुत्व के अधीन ऊर्ध्वाधर नीचे गिरते समय दो भागों में टूट जाता है जो इस प्रकार हैं - `(1)/(3)M` द्रव्यमान का पिंड B तथा `(2)/(3)M` द्रव्यमान का पिंड C, दोनों पिंडों B और C को एक साथ मिलाकर लिया गया । द्रव्यमान - केंद्र, A के द्रव्यमान केंद्र की तुलना में -
View SolutionM द्रव्यमान तथा त्रिज्या r की किसी एकसमान अर्द्धवृत्ताकार चकती का चकती के तल के लंबवत तथा चकती के केंद्र से गुजरने वाली रेखा के परितः जड़त्व - आघूर्ण होगा -
View Solutionमुल बिन्दु O पर कार्यरत बल `vecF=-Fhatk` का बिंदु `(1,-1)` के परितः बल - आघूर्ण होगा -
View Solution`m_(1)` और `m_(2)` द्रव्यमान के दो कणों के निकाय में प्रथम कण को द्रव्यमान केंद्र की ओर d दूरी विस्थापित किया जाता है । अब द्रव्यमान केंद्र को अपरिवर्तित बनाये रखने के लिए दूसरे कण को विस्थापित करना होगा -
View Solution`l` भुजा के एक वर्ग ABCD के चारों कोने पर प्रत्येक m द्रव्यमान के चार बिंदु सदृश्य पिंड रखे गए हैं । A से गुजरते-हुए तथा विकर्ण BD के समांतर अक्ष के परितः निकाय का जड़त्व - आघूर्ण होगा -
View Solution2R त्रिज्या की एक बड़ी चकती में से R त्रिज्या की एक वृत्तीय चकती इस प्रकार हटायी जाती है कि उनकी परिधि संपाती हो । यदि नई चकती का द्रव्यमान केंद्र बड़ी चकती के केंद्र से `alphaR` दूरी पर हो, तो `alpha` का मान होगा -
View Solutionकेंद्रीय बल के अंतर्गत घूर्णन कर रहे कण का कोणीय संवेग नियत रहता है, क्योंकि -
View SolutionR त्रिज्या, M द्रव्यमान तथा I जड़त्व आघूर्ण वाली एक गोलाकार समरूप वस्तु क्षैतिज `theta` से कोण बनाते नत समतल पर बिना फिसले लुढ़क रही है । उसका त्वरण होगा -
View Solutionसंलग्न चित्र में प्रदर्शित एकसमान वर्गाकार पटल ABCD जिसका केंद्र O है, के लिए सत्य संबंध है-
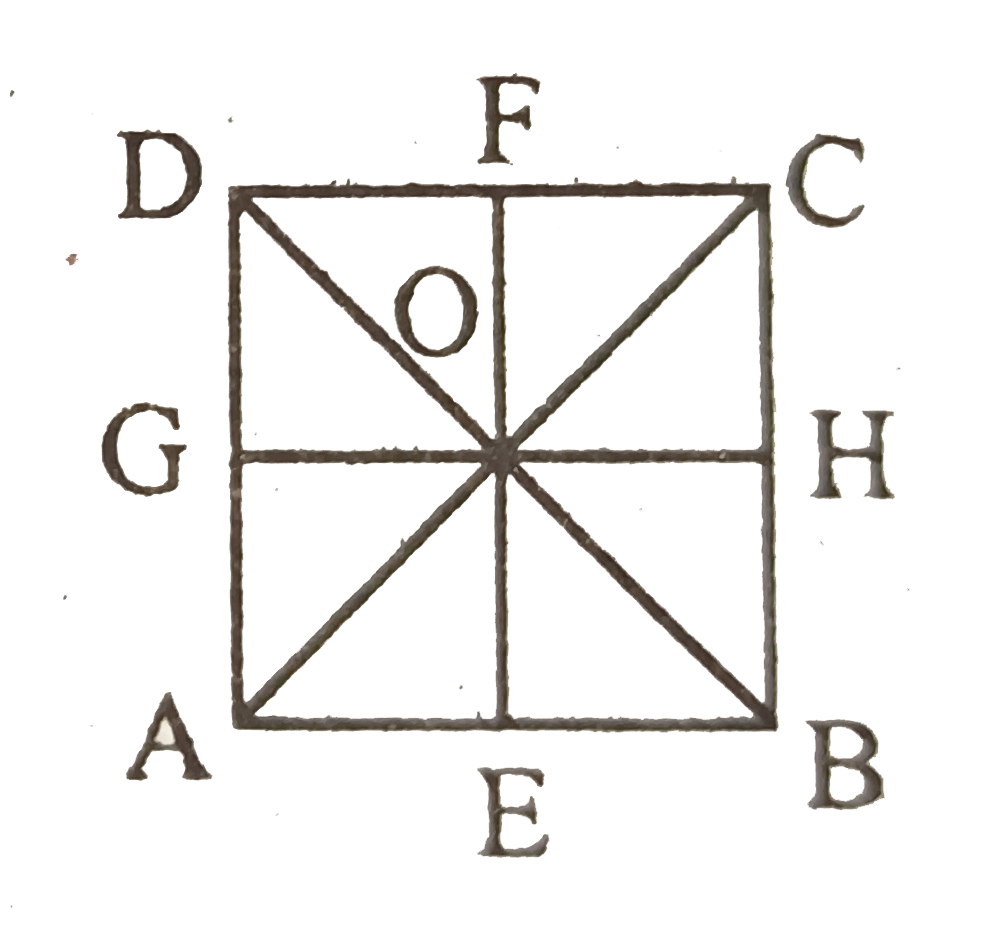
View Solutionएक पतली छड़ जिसकी लम्बाई L है, X - अक्ष के अनुदिश है तथा इसके सिरे `X = 0` तथा `X = 1` पर है । इसका रेखीय घनत्व ( द्रव्यमान / लम्बाई ) X के साथ `k((X)/(L))^(n)` के अनुसार परिवर्तित होता है , जहाँ n शून्य या कोई धनात्मक संख्या है । यदि छड़ के द्रव्यमान - केंद्र `X_(cm)` की स्थिति एवं n के बीच ग्राफ खींचे, तो निम्न में से कौन - सा ग्राफ `X_(cm)` की n पर निर्भरता को सबसे अच्छी प्रकार से प्रदर्शित करता है
View Solutionएकसमान वर्गाकार प्लेट की प्रत्येक भुजा a तथा द्रव्यमान m है । इस प्लेट के तल के लंबवत तथा इसके किसी कोने से गुजरने वाली अक्ष के परितः प्लेट का जड़त्व आघूर्ण है -
View SolutionR त्रिज्या और 9M द्रव्यमान वाली एक चकती से R/3 त्रिज्या तथा M द्रव्यमान वाली एक संकेन्द्रीय छोटी चकती निकाली जाती है । शेष बची चकती का उसके तल के लंबवत तथा केंद्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण लेगा -
View SolutionM द्रव्यमान तथा L लम्बाई की एकसमान छड़ का, उसके अक्ष जो इसकी लम्बाई के लंबवत तथा इसकी लम्बाई के मध्य बिंदु से गुजराती है, के परितः जड़त्व - आघूर्ण `I_(0)` है । इस एक सिरे से गुजरने वाले तथा लम्बाई के लंबवत अक्ष के परितः जड़त्व - आघूर्ण होगा -
View Solutionकिसी स्थिर बिंदु के परितः किसी समतल में घूर्णन करते हुए एक पिंड के कोणीय संवेग की दिशा होती है -
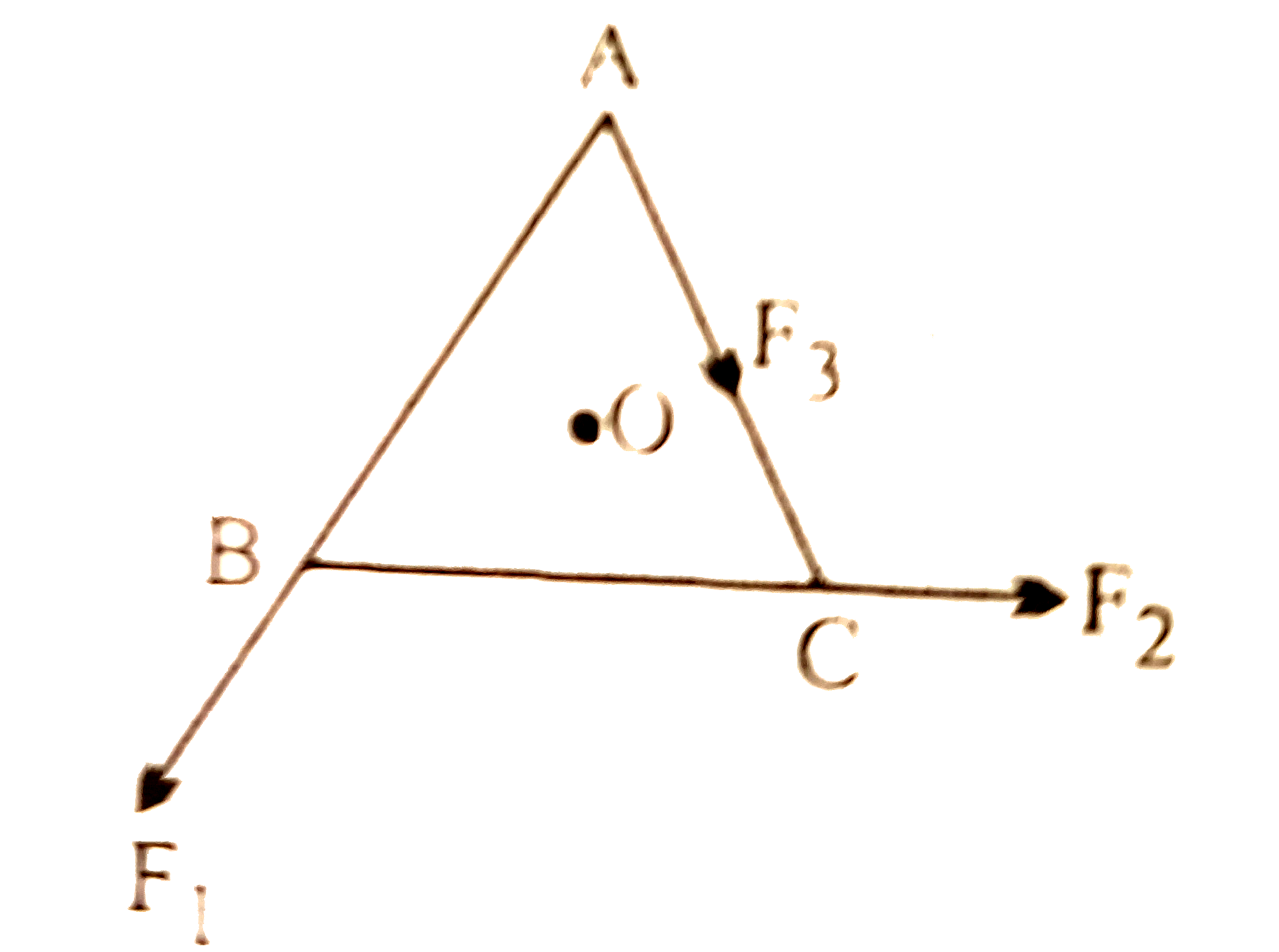
View SolutionABC एक समबाहु त्रिभुज है जिसका केंद्र O है, `vec(F_(1)), vec(F_(2))` तथा `vec(F_(3))` क्रमश AB, BC तथा AC दिशा में लगे बल हैं । यदि O के परितः कुल बल आघूर्ण शून्य हो, तो `vec(F_(3))` का मान होगा-
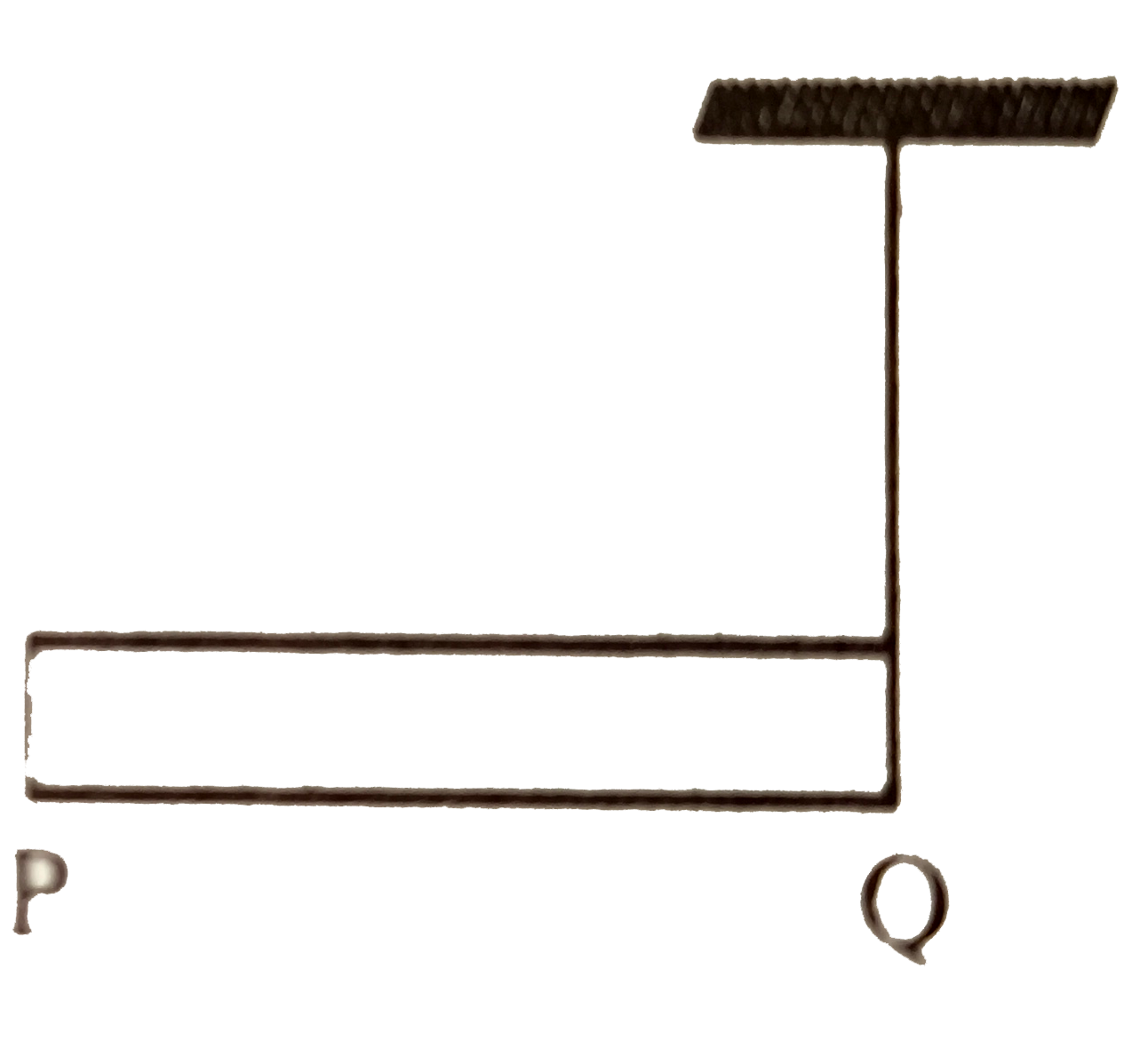
View Solutionद्रव्यमान M तथा लम्बाई L की एक छड़ PQ सिरे P से लटकी हुई है । छड़ को क्षैतिज रखने के लिए इसे Q बिंदु पर द्रव्यमान रहित डोरी से बाँध दिया जाता है । जब डोरी को काट दिया जाता है तब प्रारंभ में छड़ का कोणीय त्वरण है -
View Solutionएक छोटा कण, जो एकसमान घनत्व रखता है। प्रारंभिक वेग U - से वक्रपृष्ठ पर ऊपर की ओर लुढ़कता है ।यदि वह उच्चतम ऊँचाई `(3v^(2))/(4g)` तक पहुँचता है । तब वस्तु है -
View Solution50 किग्रा द्रव्यमान तथा 0.5 मीटर त्रिज्या का एक ठोस बेलन अपने क्षैतिज अक्ष के परितः स्वतंत्रतापूर्वक घूम सकता है । इस पर एक भारहीन रस्सी लपेटी गई है, जिसका एक सिरा इस बेलन से जुड़ा है और दूसरा सिरा मुक्त रूप से लटक रहा है । रस्सी में कितना तनाव लगाया जाए कि कोणीय त्वरण `"2 परिभ्रमण/सेकंड"^(2)` हो -
View Solutionएक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है । वह `theta` कोण से झुके नत समतल पर पहली स्थिति में बिना फिसले लुढ़कता है तथा दूसरी स्थिति में बिना लुढ़के फिसलता है । उनके त्वरण की अनुपात होगी
View Solutionएक दृढ छड़ की लम्बाई L तथा द्रव्यमान नगण्य है । इसके विपरीत सिरों पर `m_(1)` और `m_(2)` द्रव्यमान के दो बिंदु पिंड रखे गए हैं । इसे बिंदु P से जाने वाले स्वयं के अक्ष के लंबवत अक्ष के परितः घुमाया जाता है । बिंदु P की वह स्थिति, जिसके लिए छड़ को कोणीय वेग `omega_(0)` से घूर्णन कराने के लिए आवश्यक कार्य न्यूनतम होगा, है-
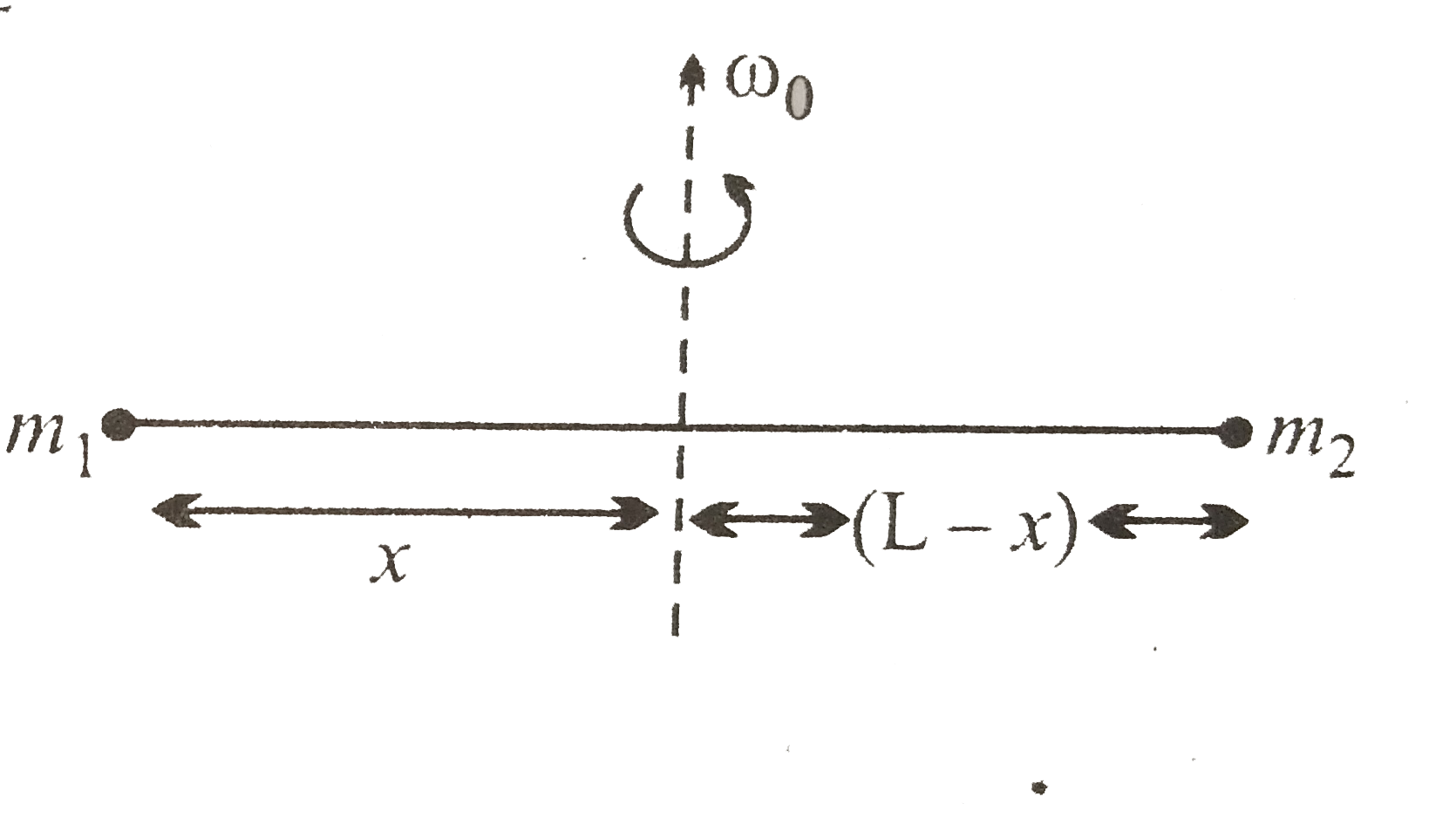
View Solutionकिसी बिंदु `vecr=2hati-6hatj-12hatk` पर एक बल `vecF=alpha hati+3hatj+6hatk` लग रहा है । `alpha` के किस मान के लिए मूल बिंदु के परितः कोणीय संवेग संरक्षित रहेगा -
View Solutionएक मोटर वाहन किसी सड़क पर 54 किमी / घंटा की चाल से चल रहा है । इसके पहियों की त्रिज्या 0.45 मीटर तथा घूर्णन अक्ष के परितः जड़त्व आघूर्ण 3 किग्रा मीटर`""^(2)` है। यदि ब्रेक लगाने के बाद वाहन को रुकने में 15 सेकंड का समय लगता हो, तो ब्रेक द्वारा पहिए पर लगा औसत बल - आघूर्ण का मान होगा-
View Solutionएक छड़ का भार W है । वह दो समांतर क्षुरधारों A और B पर टिकी है और क्षैतिज अवस्था में संतुलन में है । ( यदि A और B के बीच की दूरी d हो तथा द्रव्यमान केंद्र A से x दूरी पर हो तो A पर अभिलंब प्रतिक्रिया का मान होगा ) -
View Solutionm द्रव्यमान का एक पिंड `R_(0)` त्रिज्या के पक्ष में किसी चिकने क्षैतिज समतल पर `V_(0)` वेग से गति कर रहा है । यह पिंड एक डोरी से जुड़ा है । यह डोरी समतल पर बने चिकने छिद्र से होकर गुजरती है, जैसा कि चित्र में प्रदर्शित किया गया है । इस डोरी के तनाव को धीरे - धीरे बढ़ाया जाता है जिससे अंत में यह पिंड `R_(0)//2` त्रिज्या के वृत्ताकार पथ पर गति करने लगता है, तो गतिज ऊर्जा का अंतिम मान होगा -

View Solutionतीन सर्वसम गोलीय खोखले गोलों में से प्रत्येक का द्रव्यमान m तथा त्रिज्या r है । इन्हें चित्र में दिखाए गए अनुसार रखा गया है । XX' एक अक्ष है, जो दो गोलों को स्पर्श करता है तथा तीसरे गोले के व्यास से होकर गुजरता है । XX' अक्ष के परितः इस निकाय का जड़त्व आघूर्ण होगा-

View Solutionघूर्णन करते हुए दो पिंड A और B के द्रव्यमान क्रमश m और 2m तथा जड़त्व आघूर्ण क्रमशः `I_(A)` और `I_(B)(I_(B) gt I_(A))` हैं । इन दोनों की घूर्णन गतिज ऊर्जाएँ आपस में बराबर हैं । यदि इनके कोणीय संवेग क्रमश : `L_(A)` और `L_(B)` हों तो -
View Solutionद्रव्यमान m तथा त्रिज्या r का एक ठोस गोला अपने व्यास के परितः घूर्णन कर रहा है । उसी द्रव्यमान तथा उसी त्रिज्या का एक ठोस बेलन भी अपने ज्यामितीय अक्ष के परितः घूर्णन कर रहा है । बेलन के घूर्णन की कोणीय चाल गोले से दुगुनी है । इन दोनों की घूर्णन गतिज ऊर्जाओं का अनुपात होगा -
View Solutionएक हल्की छड़ की लम्बाई । है । इसके दो सिरों से `m_(1)` और `m_(2)`द्रव्यमान के दो पिंड संलग्न हैं । इस छड़ के लंबवत तथा द्रव्यमान केंद्र से गुजरते हुए अक्ष के परितः इस निकाय का जड़त्व आघूर्ण होगा -
View Solutionद्रव्यमान M तथा त्रिज्या R की किसी चकती से R व्यास का कोई वृत्ताकार छिद्र इस प्रकार काटा जाता है, कि उसकी नेमि चकती के केंद्र से गुजरे । चकती के शेष भाग का चकती के लंबवत तथा उसके केंद्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण होगा -
View Solutionकोई चकती और कोई ठोस गोला, जिनकी त्रिज्याएँ समान किन्तु द्रव्यमान भिन्न हैं, समान उन्नतांश और लम्बाई के दो आनत तलों पर लुढ़कते हैं । इन दोनों पिंडो में से तली पर पहले कौन पहुँचेगा -
View Solutionएक खोखले बेलन का द्रव्यमान 3 किग्रा तथा त्रिज्या 40 सेमी है । इस पर एक डोरी लपेट दी गई है । यदि इस डोरी को 30 न्यूटन बल द्वारा खींचा जाए तो बेलन का कोणीय त्वरण कितना होगा -
View Solutionनिम्नलिखित कथनों में से कौन - से कथन सही हैं । -
I. किसी पिंड का गुरुत्व केंद्र और उसका द्रव्यमान केंद्र सदैव संपाती होते हैं ।
II. किसी पिंड का द्रव्यमान केंद्र वह बिंदु होता है जहाँ पर पिंड पर लगा कुल गुरुत्वीय बल आघूर्ण शून्य होता है।
III. किसी पिंड पर लगा बलयुग्म उसमें स्थानांतरीय तथा घूर्णी दोनों प्रकार की गति उत्पन्न करता है ।
IV. यांत्रिक लाभ का मान एक से अधिक होने का तात्पर्य यह है कि कम आयाम से अधिक भार उठाया जा सकता है-
View Solutionतीन पिंड A ( एक ठोस गोला ), B ( एक पतली वृत्ताकार चकती ) और C ( एक वृत्ताकार वलय ) , जिनमें से प्रत्येक का द्रव्यमान M तथा त्रिज्या R है , समान कोणीय चाल से अपनी सममित अक्षों के परितः चक्रण कर रहे हैं । इन्हें विरामावस्था में लाने के लिए किए गए आवश्यक कार्यों (W) के लिए कौन - सा संबंध सही है -
View Solutionबिंदु `(2 ,0,-3)` पर कार्यरत बल `vecF=4hati+5htj-6hatk` का बिंदु `(2,-2,-2)` के परितः आघूर्ण होगा -
View Solutionकोई ठोस गोला मुक्त आकाश में अपनी सममिति अक्ष के परितः मुक्त रूप से घूर्णन कर रहा है । इस गोले का द्रव्यमान समान रखते हुए इसकी त्रिज्या में वृद्धि की जाती है । गोले के लिए निम्नलिखित में से कौन - सी भौतिक राशि नियत रहेगी -
View Solutionलम्बाई `l` और द्रव्यमान `m` की एक पतली एकसमान छड़ अपने एक सिरे से गुजर रहे क्षैतिज अक्ष पर स्वतन्त्र रूप से दोलायमान है । इसकी अधिकतम कोणीय चाल `omega` है । इसका द्रव्यमान केंद्र किस महत्तम ऊँचाई तक उठेगा
View Solutionएक घर्षणहीन बियरिंग पर एक घिरनी के चारों ओर एक डोरी को लपेटकर द्रव्यमान m लटकाया गया है । घिरनी का द्रव्यमान m तथा R त्रिज्या है । यह मान लें कि घिरनी एक पूर्ण एकसमान वृत्तीय चकती है । यदि डोरी घिरनी पर नहीं फिसलती तब द्रव्यमान का त्वरण है-
View Solutionएक द्विपरमाणुक अणु `m_(1)` तथा `m_(2)` के दो द्रव्यमानों से बना है जो कि दूरी r पर है । यदि कोणीय संवेग क्वाण्टीकरण के बोर के नियम को लगाकर हम इसकी घूर्णन ऊर्जा की गणना करें , तब इसकी ऊर्जा दी जाएगी - (n एक पूर्णाक है )
View Solutionकोणीय वेग `omega_(0)` से घूर्णन कर रहे द्रव्यमान m और त्रिज्या r के एक लूप को एक खुरदुरे क्षैतिज तल पर रखा गया है । लूप के केंद्र का प्रारंभिक वेग शून्य है । जब यह स्लिप करना बंद कर दे, तब लूप के केंद्र का वेग क्या होगा
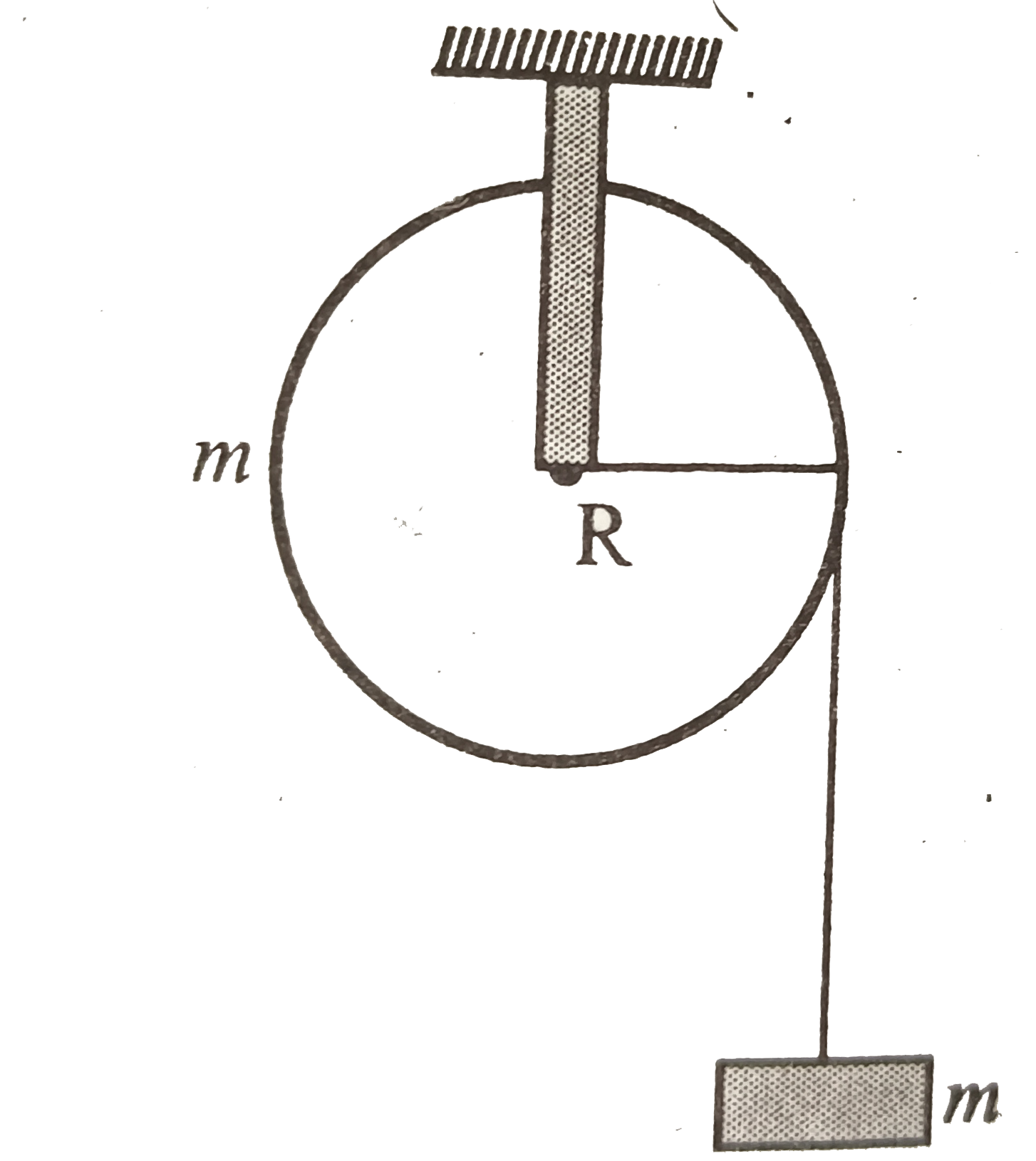
View Solutionत्रिज्या R तथा द्रव्यमान m के एकसमान खोखले बेलन के चारों ओर एक द्रव्यमानहीन डोरे से एक द्रव्यमान अवलंबित है । यदि डोरी बेलन पर फिसलती नहीं हो, तो छोड़े जाने पर द्रव्यमान किस त्वरण से गिरेगा -
View Solutionलम्बाई `l` की एक अवितान्य डोरी से बँधे द्रव्यमान m एक गोलक को एक ऊर्ध्वाधर आधार से लटकाया गया है । गोलक ऊर्ध्वाधर आधार के आसपास कोणीय चाल रेडियन ( सेकंड से एक क्षैतिज वृत्त में घूर्णन करता है । निलंबन बिंदु के आसपास )-
View Solutionकिसी एकसमान ठोस शंकु के द्रव्यमान केंद्र की उसके शीर्ष से दूरी `z_(0)` है । यदि शंकु के आधार की त्रिज्या R तथा शंकु की ऊँचाई h हो, तो `z_(0)` का मान होगा -
View Solutionकिसी ठोस गोले का द्रव्यमान M तथा R त्रिज्या है । इससे अधिकतम संभव आयतन का एक घन काट लिया जाता है । यदि घन का घूर्णन अक्ष इसके केंद्र से गुजरता हो तथा इसके एक फलक के लंबवत हो, तो घन का जड़त्व आघूर्ण कितना होगा-
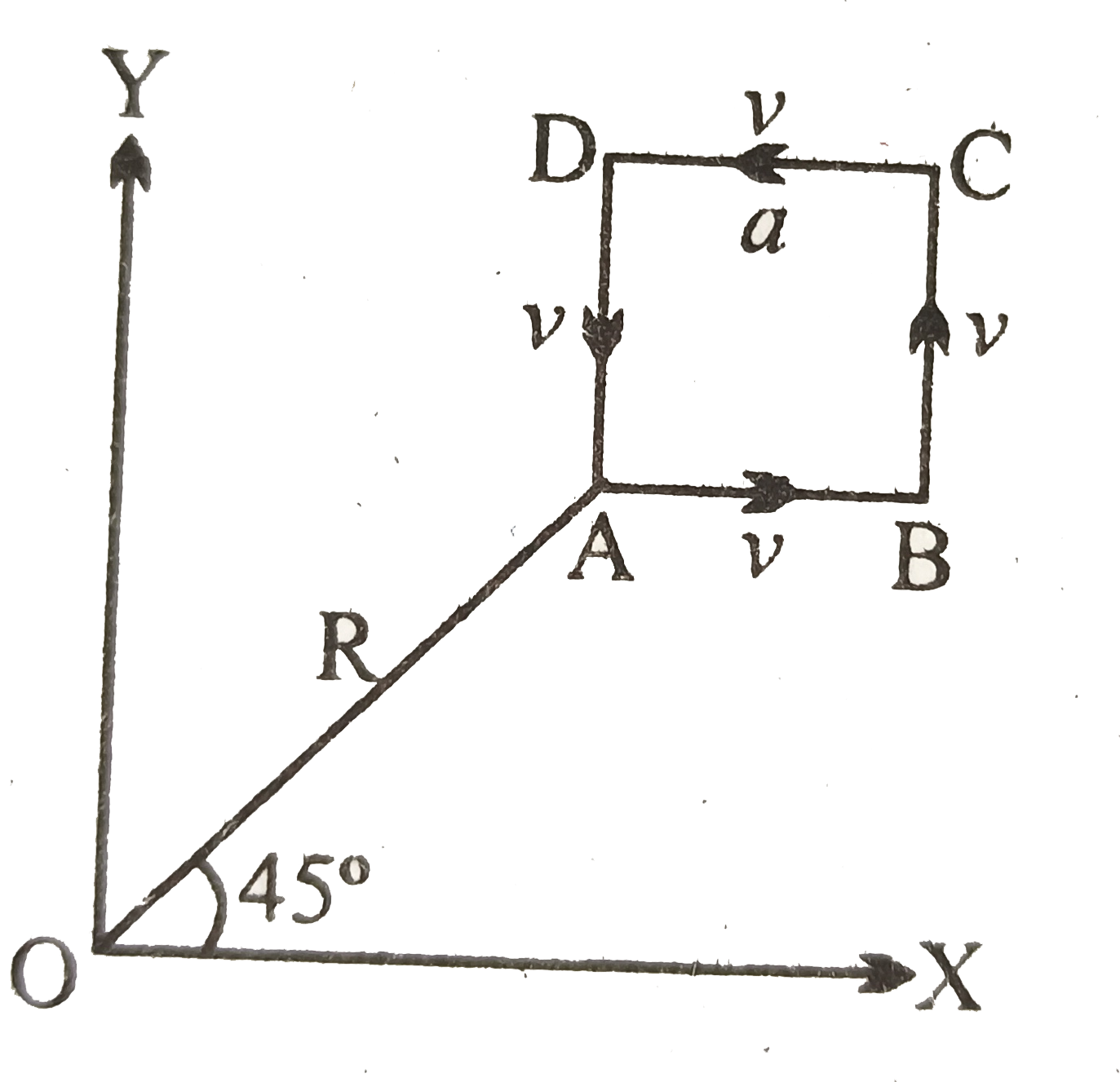
View Solutionचित्र में XY - तल में भुजा a का वर्ग ABCD है । m द्रव्य-मान का एक कण इस वर्ग की भुजा पर एकसमान वेग v से चल रहा है । तब निम्न में से कौन - सा कथन, इस कण के मूलबिंदु के परितः कोणीय संवेग L के लिए गलत है -
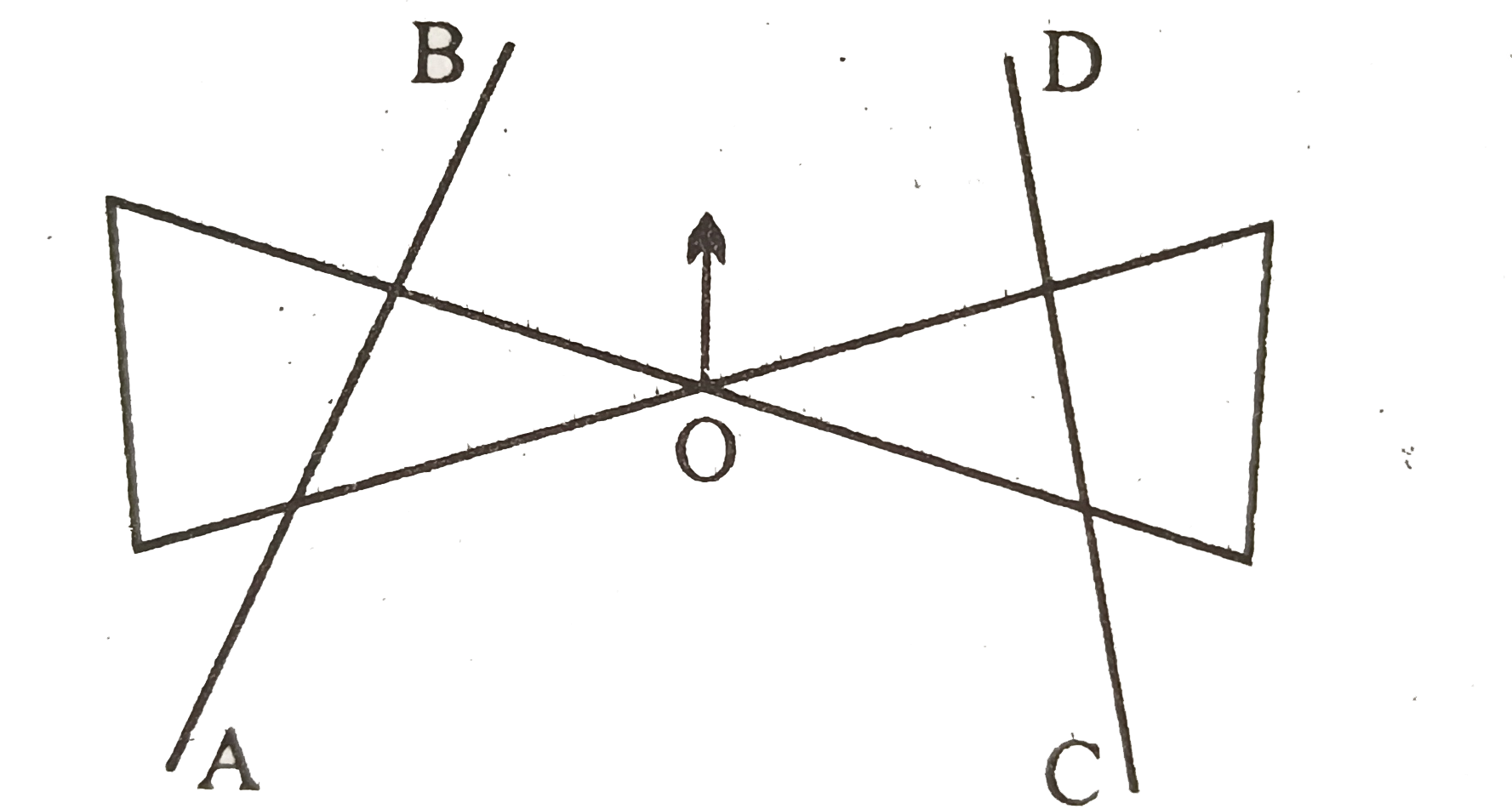
View Solutionदो शंकुओं को उनके शीर्ष O पर जोड़कर एक रोलर बनाया गया है और उसे AB तथा CD रेल पर असममित रखा गया है । रोलर का अक्ष CD के लंबवत है और O दोनों रेलों के बीचोंबीच है । हल्के से धकेलने पर रोलर रेल पर इस प्रकार लुढ़कना प्रारंभ करता है , कि O का चालन CD के समांतर है । गति प्रारंभ होने के पश्चात यह रोलर -
View Solutionत्रिज्या R तथा लम्बाई `l` के एकसमान बेलन का उसके अभिलंब द्विभाजक के सापेक्ष जड़त्व आघूर्ण `I` है । जड़त्व आघूर्ण के निम्नतम मान के लिए अनुपात `l//R` का मान क्या होगा -
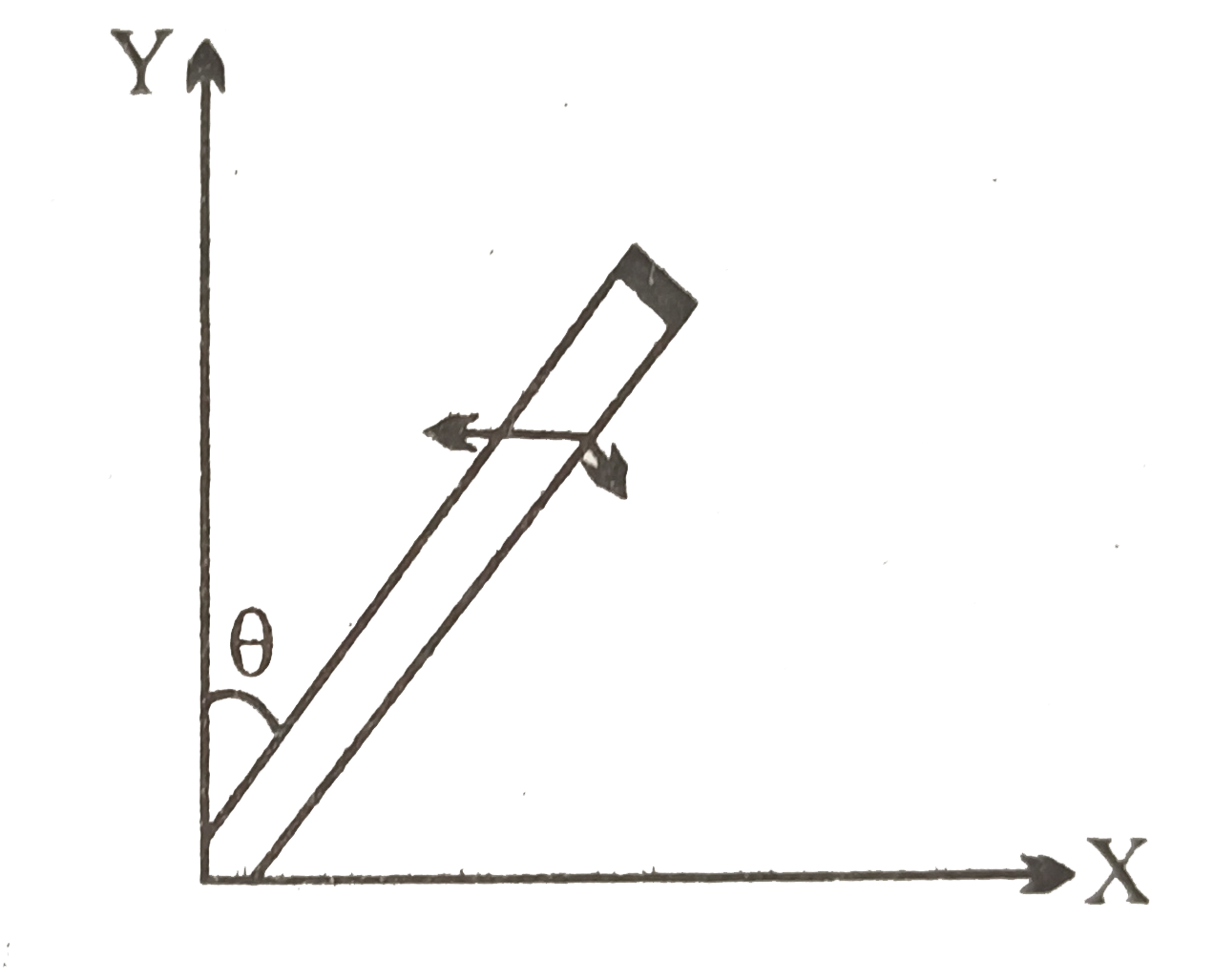
View Solutionद्रव्यमान M तथा लम्बाई `l` की पतली एवं एकसमान एक छड़ का एक सिरा धुराग्रस्त है जिससे कि यह ऊर्ध्वाधर समतल में घूम सकती है । धुरा का घर्षण नगण्य है । छड़ के दूसरे सिरे को धुरी के ऊपर ऊर्ध्वाधर रखकर छोड़ दिया जाता है । जब छड़ ऊर्ध्व से `theta` कोण बनाती है तब उसका कोणीय त्वरण होगा -
View Solutionसात वृत्ताकार आदर्श चकतियों को चित्रानुसार समायोजित किया गया है । प्रत्येक चकती का द्रव्यमान M तथा त्रिज्या R है । इस व्यवस्था का इसके तल के लंबवत तथा बिंदु P से जाने वाले अक्ष के परितः जड़त्व आघूर्ण होगा -
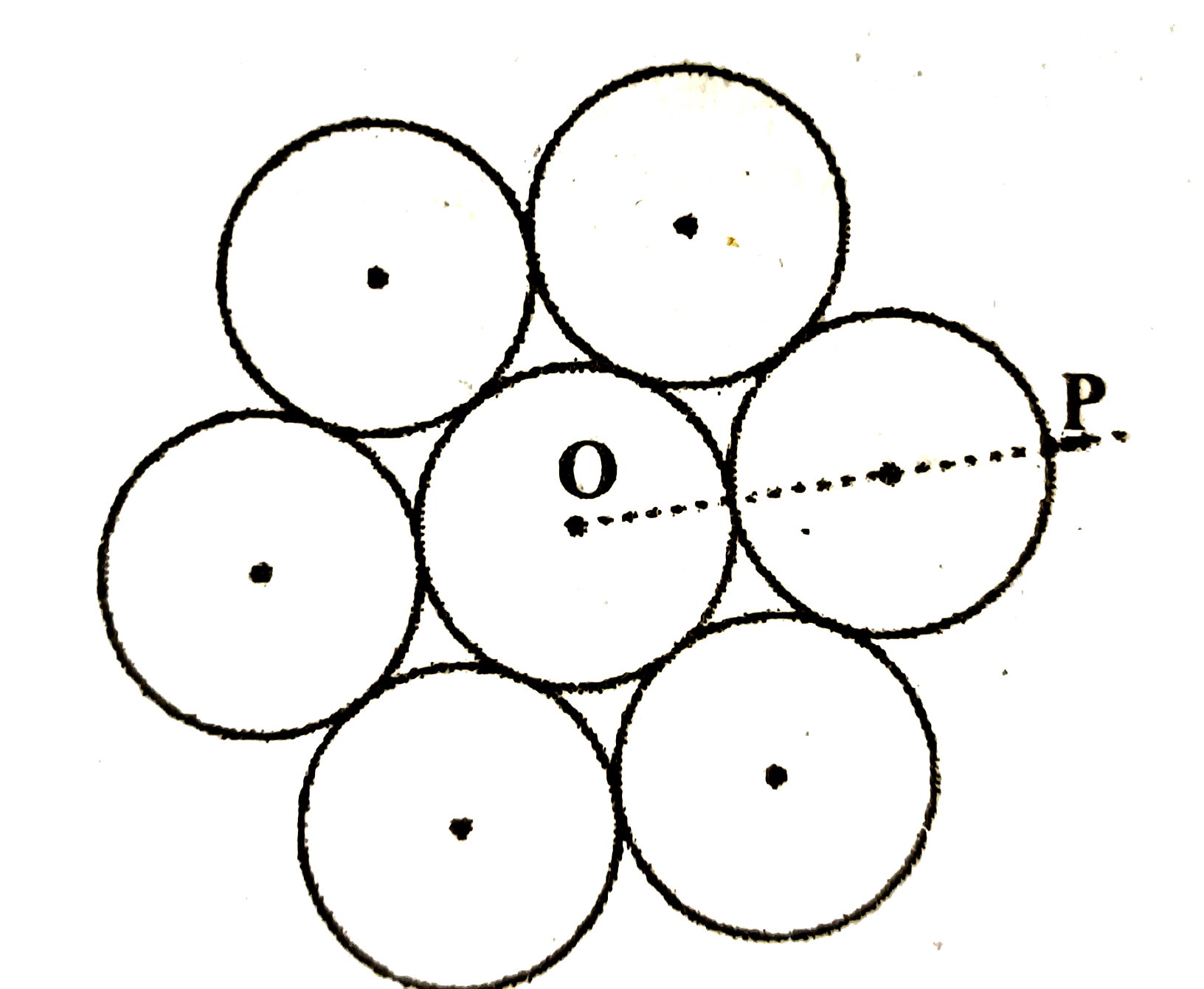
View SolutionR त्रिज्या तथा 9M द्रव्यमान की एकसमान चकती से `(R)/(3)` त्रिज्या की छोटी चकती के चित्र में दर्शाए अनुसार काट लिया जाता है । शेष चकती का इसके तल के लंबवत तथा केंद्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण होगा -

View Solutionआपको समान भार और समान मोटाई की दो वृत्तीय चक्रिका दी जाती है ।चक्रिकाएँ अलग - अलग धातु, जिनका घनत्व `d_(1)` तथा `d_(2)` हैं , की बनी हैं । उनकी त्रिज्याएँ क्रमश : `R_(1)` तथा `R_(2)` हैं । उस चक्रिका का केंद्रीय अक्ष के प्रति जड़त्व आघूर्ण अधिक होगा जिसके लिए
View Solution`"2.0 रेडियन/सेकंड"^(2)` के समान त्वरण से एक पहिया घूर्णन करता है । यदि पहिया विराम से घूर्णन प्रारम्भ करता है तो प्रथम 10 सेकंड में पूरे होने वाले चक्करों की संख्या होगी लगभग -
View Solutionद्रव्यमान M तथा त्रिज्या r का एक वृत्ताकार पतला वलय अपने अक्ष के परितः स्थिर कोणीय वेग `omega` से घूम रहा है । दो वस्तुएँ जिनमें प्रत्येक का द्रव्यमान M है वलय के किसी व्यास के विपरीत सिरों पर धीरे से चिपका दी जाती है । ऐसा करने पर वलय का कोणीय वेग क्या हो जाएगा ?
View Solutionm द्रव्यमान के कण को क्षैतिज से `45^(@)` के कोण पर वेग `v` प्रक्षेपित किया जाता है । जब कण महत्तम ऊँचाई पर है । प्रक्षेपण - बिंदु के परितः कण के कोणीय संवेग का मान होगा ( g = गुरुत्वीय त्वरण )-
View SolutionR त्रिज्या वाली एक चकती से r त्रिज्या का समकेंद्रीय वित्तीय भाग निकाल देने पर एक वलयाकार, चकती बच जाती है, जिसका द्रव्यमान M है । बची हुई वलयाकार चकती का जड़त्व आघूर्ण उसके तल से लंबवत तथा उसके गुरुत्व केंद्र से गुजरने वाले अक्ष के परितः होगा -
View Solutionm द्रव्यमान का एक पिंड r त्रिज्या के वृत्ताकार पथ में गति कर रहा है । यदि इसका कोणीय संवेग L हो तो कण पर लगने वाला अभिकेंद्री बल होगा -
View SolutionX - अक्ष से `theta` कोण पर द्रव्यमान m के एक छोटे कण को एक प्रारंभिक वेग `v_(0)` से XY - तल में प्रक्षेपित किया जाता है जैसा कि चित्र में दर्शाया गया है । समय `t lt (v_(0) sin theta)/(g)` के लिए कण का कोणीय संवेग होगा -
जहाँ `hati, hatj` और `hatk` क्रमश : X-अक्ष, Y-अक्ष और Z-अक्ष के अनुदिश एकांक सदिश हैं -
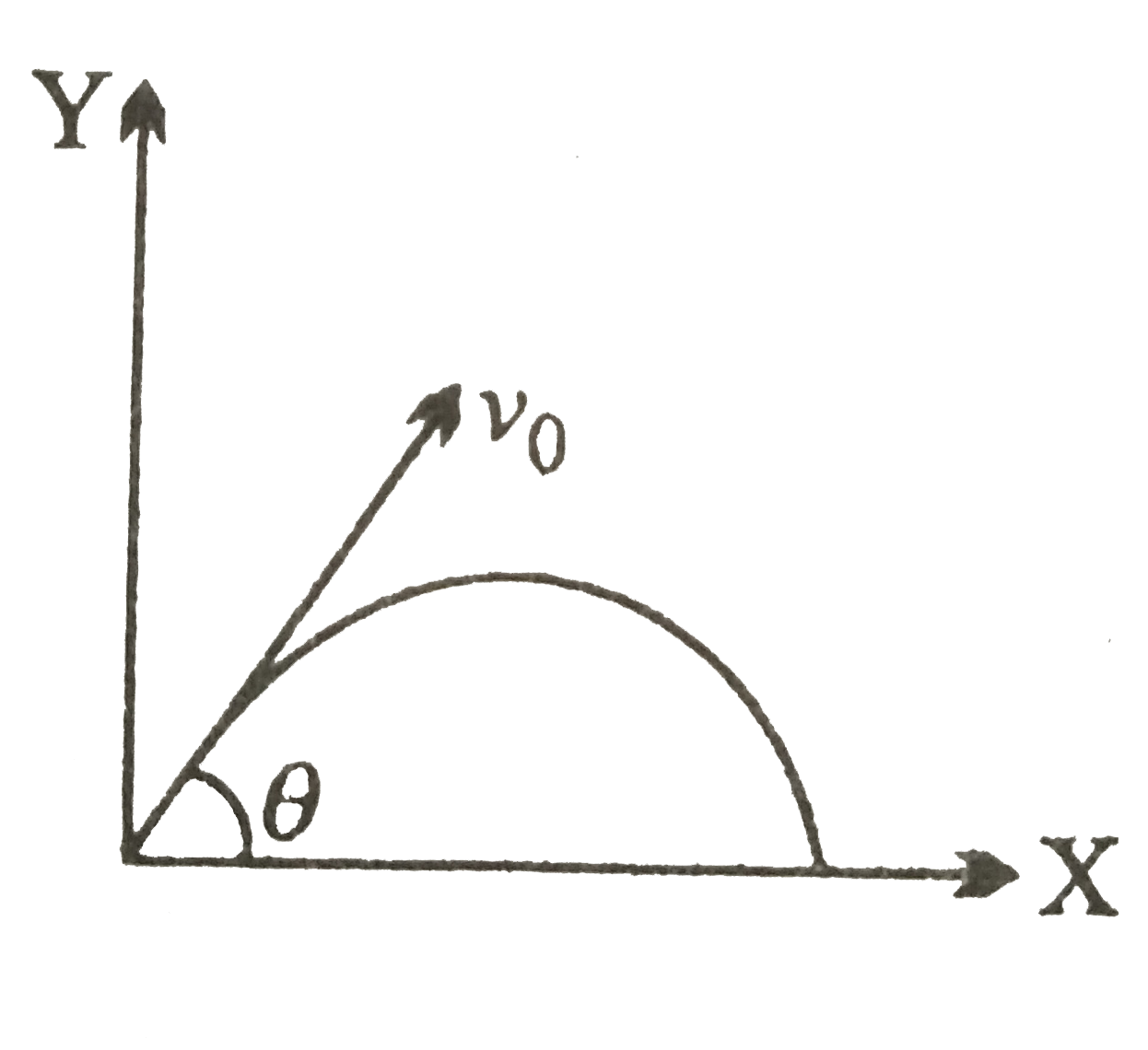
View Solution
बहुविकल्पीय प्रश्न questions and complete solutions for chapter कणों के निकाय की गति और घुर्णो गति of NAVBODH PHYSICS (HINDI) of Class 11
All Exercises from NAVBODH PARIKSHA SAAR Class 11 PHYSICS कणों के निकाय की गति और घुर्णो गति
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर
- अभ्यासार्थ प्रश्न (अति लघु उत्तरीय प्रश्न/एक शब्द/एक वाक्य )
- अभ्यासार्थ प्रश्न (उचित संबंध जोड़िए - )
- अभ्यासार्थ प्रश्न (दीर्घ उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (मूल्य आधारित प्रश्न )
- अभ्यासार्थ प्रश्न (रिक्त स्थानों की पूर्ति कीजिए - )
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (वस्तुनिष्ठ प्रश्न ) (बहुविकल्पीय प्रश्न )
- अभ्यासार्थ प्रश्न (सत्य/असत्य लिखिए - )
- आंकिक उदाहरण
- आंकिक उदाहरण प्लस
- आंकिक प्रश्न
- उदाहरण
- तथ्यात्मक प्रश्न
- बहुविकल्पीय प्रश्न
- बोधात्मक प्रश्न
- बोधात्मक प्रश्न प्लस