Complete Solutions to NCERT पाठ्यपुस्तक के प्रश्नोत्तर of chapter कणों के निकाय की गति और घुर्णो गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | कणों के निकाय की गति और घुर्णो गति |
| NAVBODH PARIKSHA SAAR | NCERT पाठ्यपुस्तक के प्रश्नोत्तर |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
एकसमान द्रव्यमान घनत्व के निम्नलिखित पिंडों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए-
( a ) गोला, ( b ) सिलिंडर, ( c ) छल्ला तथा ( d ) घन ।
क्या किसी पिंड का द्रव्यमान केंद्र आवश्यक रूप से उस पिंड के भीतर स्थित होता है ?
View Solution`HCl` अणु में दो परमाणुओं के नाभिकों के बीच पृथकन लगभग `a.27Å(1Å=10^(-10)m)` है । इस अणु के द्रव्यमान केंद्र की लगभग अवस्थिति ज्ञात कीजिए । यह ज्ञात है कि क्लोरीन का परमाणु हाइड्रोजन के परमाणु की तुलना में 35.5 गुना भारी होता है तथा किसी परमाणु का समस्त द्रव्यमान उसके नाभिक पर केंद्रित होता है |
View Solutionकोई बच्चा किसी चिकने क्षैतिज फर्श पर एकसमान चाल से गतिमान किसी लंबी ट्राली के एक सिरे पर बैठा है । यदि बच्चा खड़ा होकर ट्राली पर किसी भी प्रकार से दौड़ने लगता है, तब निकाय ( ट्राली `+` बच्चा ) के द्रव्यमान केंद्र की चाल क्या है ?
View Solutionदर्शाइए कि `veca` एवं `vecb` के बीच बने त्रिभुज का क्षेत्रफल `veca xx vecb` के परिमाण का आधा है ।
View Solutionदर्शाइए कि `veca.(vecb xx vec c)` का परिमाण तीन सदिशों `veca, vecb` एवं `vec c` से बने समांतर षट्फलक के आयतन के बराबर है ।
View Solutionएक कण जिसके स्थिति संदीश `vecr` के X,Y,Z- अक्षों के अनुदिश अवयव क्रमशः x, y, z हैं , और रेखीय संवेग सदिश `vecp` के अवयव `p_(x),p_(y),p_(z)` हैं, के कोणीय संवेग `vecL` के अक्षों के अनुदिश अवयव ज्ञात कीजिए । दर्शाइए कि यदि कण केवल XY - तल में ही गतिमान हो तो कोणीय संवेग का केवल Z - अवयव ही होता है ।
View Solutionदो कण जिनमें से प्रत्येक का द्रव्यमान m एवं चाल v है d दूरी पर, समांतर रेखाओं के अनुदिश, विपरीत दिशाओं में चल रहे हैं । दर्शाइए कि इस द्विकण निकाय का सदिश कोणीय संवेग समान रहता है, चाहे हम जिस बिंदु के परितः कोणीय संवेग लें ।
View SolutionW भार की एक असमांग छड़ को, उपेक्षणीय भार वाली दो डोरियों से चित्र में दर्शाये अनुसार लटका कर विरामावस्था में रखा गया है । डोरियों द्वारा ऊर्ध्वाधर से बने कोण क्रमश: `36.9^(@)` एवं `53.1^(@)` हैं । छड़ 2 m लम्बाई की है । छड़ के बाएँ सिरे से इसके गुरुत्व केंद्र की दूरी d ज्ञात कीजिए ।
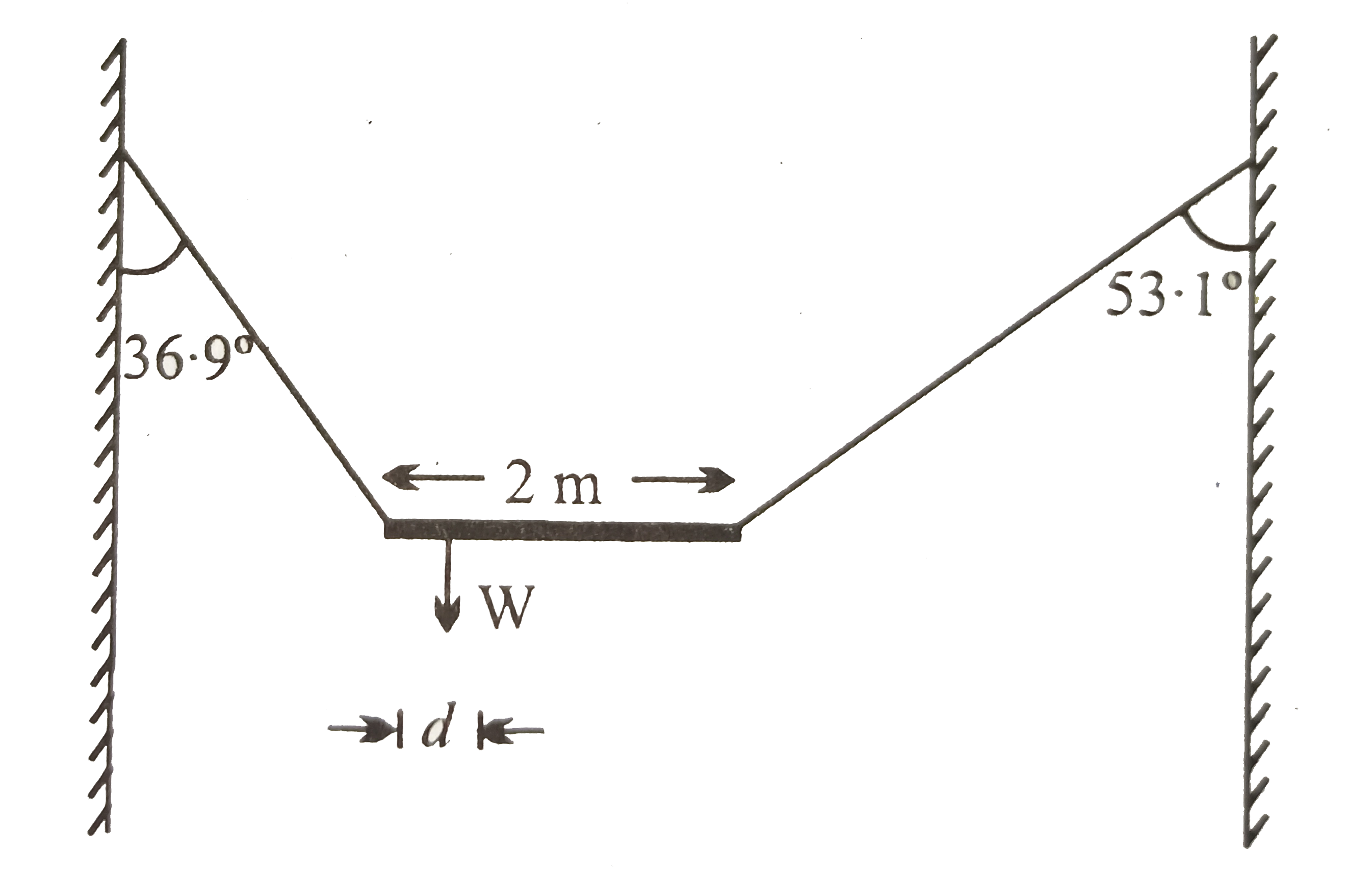
View Solutionएक कार का भार 1800 kg है । इसकी अगली और पिछली धुरियों के बीच की दूरी 1.8 m है । इसका गुरुत्व केंद्र, अगली धुरी से 1.05 m पीछे है । समतल धरती द्वारा इसके प्रत्येक अगले और पिछले पहियों पर लगने वाले बल की गणना कीजिए ।
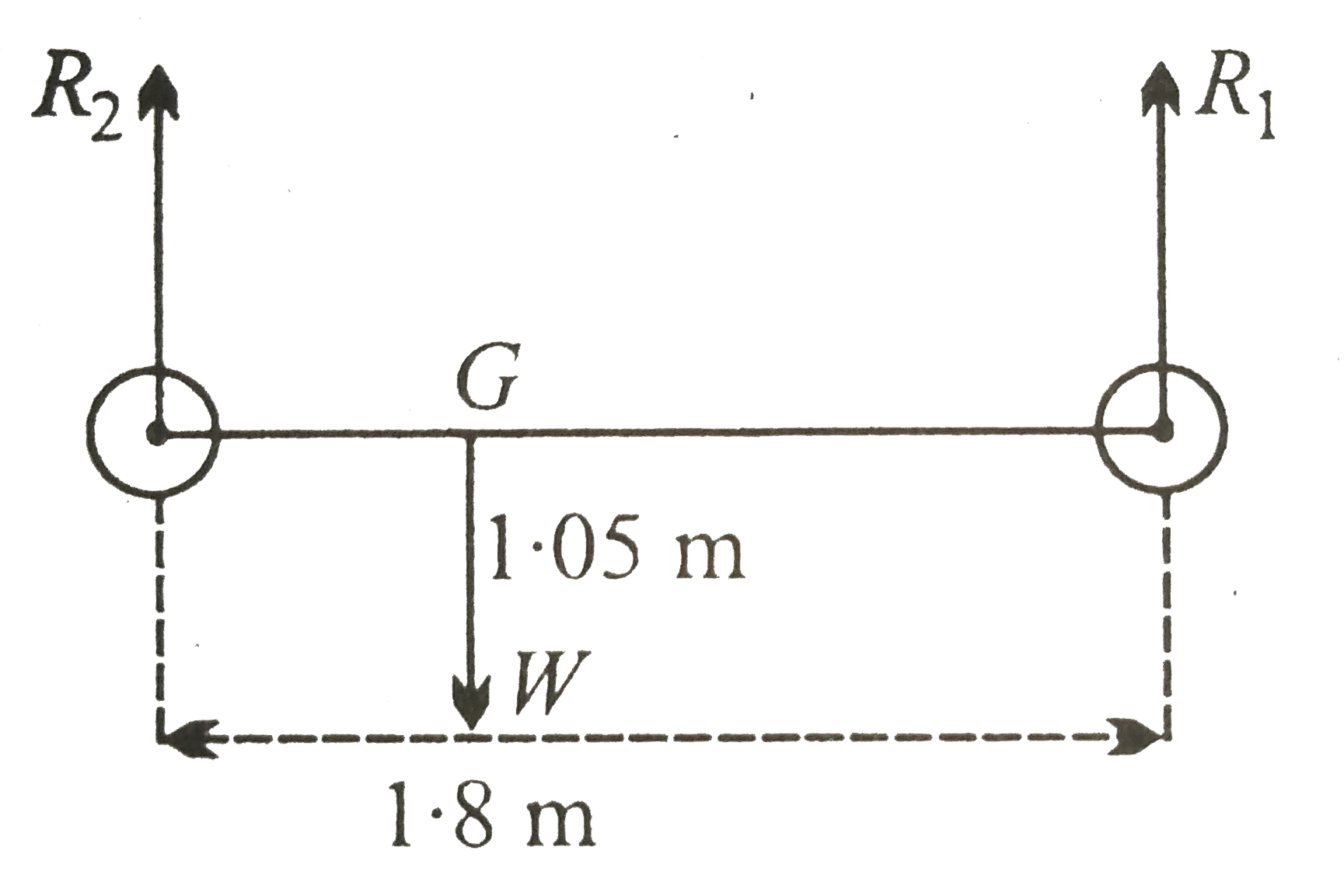
View Solution( a ) किसी गोले का, इसके किसी व्यास के परितः जड़त्व आघूर्ण `2MR^(2)//5` है, जहाँ M गोले का द्रव्यमान एवं R इसकी त्रिज्या है । गोले पर खींची गई स्पर्श रेखा के परितः इसका जड़त्व आघूर्ण ज्ञात कीजिए ।
View Solution( b ) M द्रव्यमान एवं R त्रिज्या वाली किसी डिस्क का इसके किसी व्यास के परितः जड़त्व आघूर्ण `MR^(2)//4` है । डिस्क के लंबवत इसकी कोर से गुजरने वाली अक्ष के परितः इस चकती का जड़त्व आघूर्ण ज्ञात कीजिए ।
View Solutionसमान द्रव्यमान और त्रिज्या के एक खोखले बेलन और एक ठोस गोले पर समान परिमाण के बल आघूर्ण लगाए गए हैं । बेलन अपनी सामान्य सममित अक्ष के परितः घूम सकता है और गोला अपने केंद्र से गुजरने वाली किसी अक्ष के परितः एक दिए गए समय के बाद दोनों में कौन अधिक कोणीय चाल प्राप्त कर लेगा ? -
View Solution20 kg द्रव्यमान का कोई ठोस सिलिंडर अपने अक्ष के परितः `"100 rad s"^(-1)` की कोणीय चाल से घूर्णन कर रहा है । सिलिंडर की त्रिज्या 0.25m है । सिलिंडर के घूर्णन से संबद्ध गतिज ऊर्जा क्या है ? सिलिंडर का अपने अक्ष के परितः कोणीय संवेग का परिमाण क्या है ?
View Solution( a ) कोई बच्चा किसी घूर्णिका ( घूर्णीमंच ) पर अपनी दोनों भुजाओं को बाहर की ओर फैलाकर खड़ा है । घूर्णिका को 40 rev/min की कोणीय चाल से घूर्णन कराया जाता है । यदि बच्चा अपने हाथों को वापस सिकोड़ कर अपना जड़त्व आघूर्ण अपने आरंभिक जड़त्व आघूर्ण का 2/5 गुना कर लेता है, तो इस स्थिति में उसकी कोणीय चाल क्या होगी ? यह मानिए कि घूर्णिका की घूर्णन गति घर्षणरहित है ।
View Solution( b ) यह दर्शाइए कि बच्चे की घूर्णन की नयी गतिज ऊर्जा उसकी आरंभिक घूर्णन की गतिज ऊर्जा से अधिक है । आप गतिज ऊर्जा में हुई इस वृद्धि की व्याख्या किस प्रकार करेंगे ?
View Solution3 kg द्रव्यमान तथा 40 cm त्रिज्या के किसी खोखले सिलिंडर पर कोई नगण्य द्रव्यमान की रस्सी लपेटी गई है । यदि रस्सी को 30 न्यूटन से खींचा जाए तो सिलिंडर का कोणीय त्वरण क्या होगा ? यह मानिए कि इस प्रकरण में कोई फिसलन नहीं है |
View Solutionकिसी घूर्णक ( रोटर ) की `"200 rad s"^(-1)` की एकसमान कोणीय चाल बनाए रखने के लिए एक इंजन द्वारा 180 Nm का बल आघूर्ण प्रेषित करना आवश्यक होता है । इंजन के लिए आवश्यक शक्ति ज्ञात कीजिए । ( नोट : घर्षण की अनुपस्थिति में एकसमान कोणीय वेग होने में यह समाविष्ट है कि बल आघूर्ण शून्य है । व्यवहार में लगाए गए बल आघूर्ण की आवश्यकता घर्षणी बल आघूर्ण को निरस्त करने के लिए होती है । ) यह मानिए कि इंजन की दक्षता `100 %` है ।
View SolutionR त्रिज्या वाली समांग डिस्क से R/2 त्रिज्या का एक वृत्ताकार भाग काट कर निकाल दिया गया है । इस प्रकार बने वृत्ताकार सुराख का केंद्र मूल डिस्क के केंद्र से R/2 दूरी पर है । अवशिष्ट डिस्क के गुरुत्व केंद्र की स्थिति ज्ञात कीजिए ।
View Solutionएक मीटर छड़ के केंद्र के नीचे क्षुर- धार रखने पर वह इस पर संतुलित हो जाती है जब दो सिक्के, जिनमें प्रत्येक का द्रव्यमान 5g है, 12.0 cm के चिन्ह पर एक के ऊपर एक रखे जाते हैं तो छड़ 45.0 cm चिन्ह पर संतुलित हो जाती है । मीटर छड़ का द्रव्यमान क्या है ?
View Solutionएक ठोस गोला, भिन्न नति के दो आनत तलों पर एक ही ऊँचाई से लुढ़कने दिया जाता है । ( a ) क्या वह दोनों बार समान चाल से तली में पहुँचेगा ?
View Solutionएक ठोस गोला, भिन्न नति के दो आनत तलों पर एक ही ऊँचाई से लुढ़कने दिया जाता है । ( b ) क्या उसको एक तल पर लुढ़कने में दूसरे से अधिक समय लगेगा ?
View Solutionएक ठोस गोला, भिन्न नति के दो आनत तलों पर एक ही ऊँचाई से लुढ़कने दिया जाता है । क्या उसको एक तल पर लुढ़कने में दूसरे से अधिक समय लगेगा ( c ) यदि हाँ, तो किस पर और क्यों ?
View Solution2m त्रिज्या के एक वलय ( छल्ले ) का भार 100 kg है । यह एक क्षैतिज फर्श पर इस प्रकार लोटनिक गति करता है की इसके द्रव्यमान केंद्र की चाल 20cm /s हो । इसको रोकने के लिए कितना कार्य करना होगा ?
View Solutionऑक्सीजन अणु का द्रव्यमान `5.30xx10^(-26)kg` है तथा इसके केंद्र से होकर गुजरने वाली और इसके दोनों परमाणुओं को मिलाने वाली रेखा के लंबवत अक्ष के परितः जड़त्व आघूर्ण `1.94xx10^(-46)km^(2)` है । मान लीजिए कि गैस के ऐसे अणु की औसत चाल `500 m//s` है और इसके घूर्णन की गतिज ऊर्जा, स्थानांतरण की गतिज ऊर्जा की दो तिहाई है । अणु का औसत कोणीय वेग ज्ञात कीजिए ।
View Solutionएक बेलन `30^(@)` कोण बनाते आनत तल पर लुढकता हुआ ऊपर चढ़ाता है । आनत तल की तली में बेलन के द्रव्यमान केंद्र की चाल `5m//s` है ।
( a ) आनत तल पर बेलन कितना ऊपर जाएगा ?
View Solutionएक बेलन `30^(@)` कोण बनाते आनत तल पर लुढकता हुआ ऊपर चढ़ाता है । आनत तल की तली में बेलन के द्रव्यमान केंद्र की चाल `5m//s` है ।
(b) वापस तली तक लौट आने में इसे कितना समय लगेगा ।
View Solutionजैसा चित्र में दिखाया गया है, एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्ज़ा लगा कर जोड़ा गया है । इन्हें ठीक बीच में 0.5m लंबी रस्सी DE द्वारा बाँधा गया है । सीढ़ी BA के अनुदिश B से 1.2m की दूरी पर स्थित बिंदु F से 40kg का एक भार लटकाया गया है । यह मानते हुए कि फर्श घर्षण रहित है और सीढ़ी का भार उपेक्षणीय है, रस्सी में तनाव और सीढ़ी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए । (`g=9.8m//s^(2)`लीजिए )
[संकेत : सीढ़ी के दोनों ओर के संतुलन पर अलग-अलग विचार कीजिए )
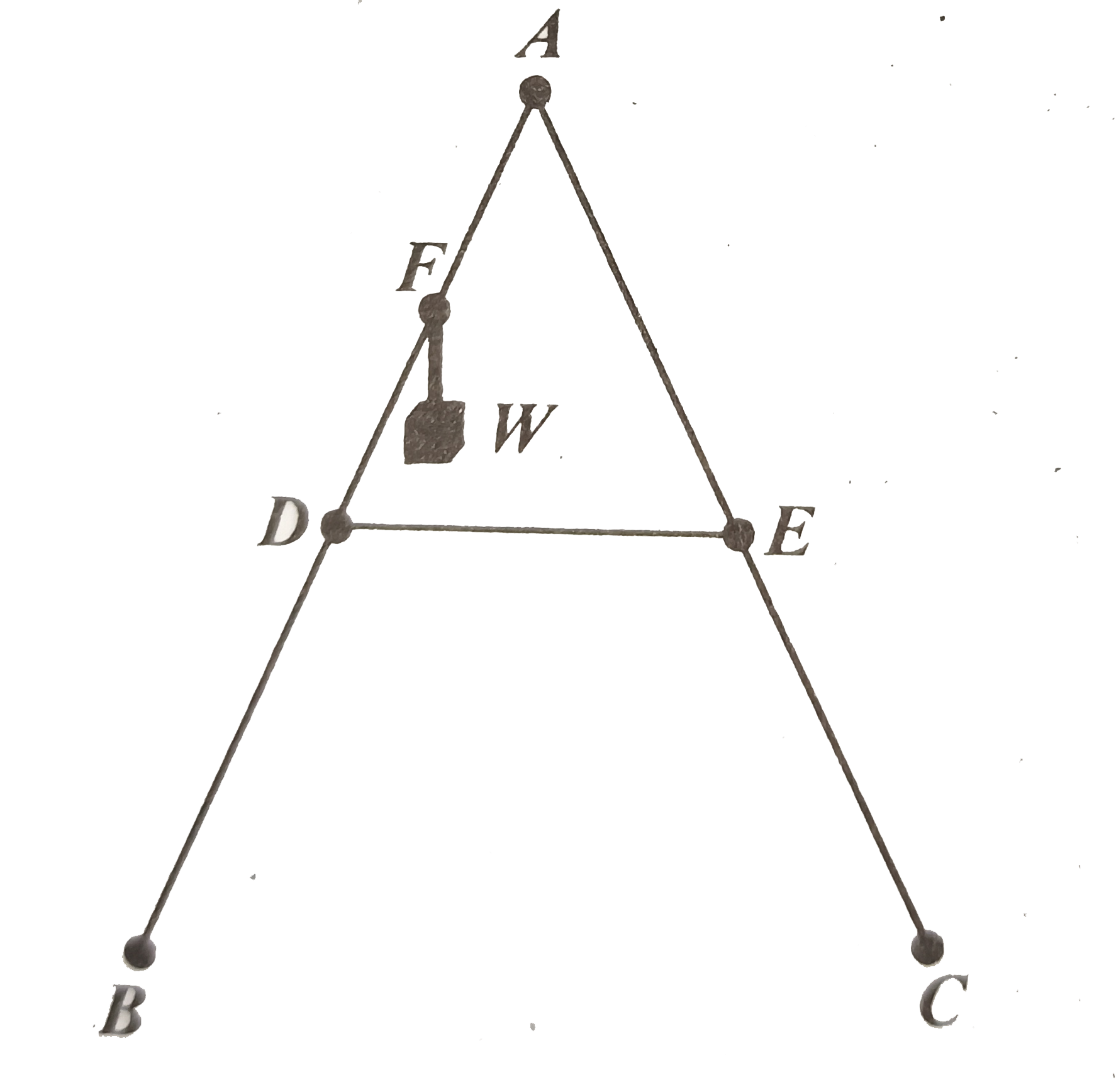
View Solutionकोई व्यक्ति एक घूमते हुए प्लेटफार्म पर खड़ा है । उसने अपनी दोनों बाहें फैला राखी हैं और उनमें से प्रत्येक ने 5 kg भार पकड़ रखा है । प्लेटफार्म का कोणीय चाल 30 rev/min है । फिर वह व्यक्ति बाहों को अपने शरीर के पास ले आता है जिससे घूर्णन अक्ष से प्रत्येक भार की दूरी 90 cm से बदल कर 20 cm हो जाती है । प्लेटफार्म सहित व्यक्ति के जड़त्व आघूर्ण का मान `"7.6 kg m"^(2)` ले सकते हैं ।
( a ) उसका नया कोणीय वेग क्या है ? ( घर्षण की उपेक्षा कीजिए ) ।
View Solutionकोई व्यक्ति एक घूमते हुए प्लेटफार्म पर खड़ा है । उसने अपनी दोनों बाहें फैला राखी हैं और उनमें से प्रत्येक ने 5 kg भार पकड़ रखा है । प्लेटफार्म का कोणीय चाल 30 rev/min है । फिर वह व्यक्ति बाहों को अपने शरीर के पास ले आता है जिससे घूर्णन अक्ष से प्रत्येक भार की दूरी 90 cm से बदल कर 20 cm हो जाती है । प्लेटफार्म सहित व्यक्ति के जड़त्व आघूर्ण का मान `"7.6 kg m"^(2)` ले सकते हैं ।
( b ) क्या इस प्रक्रिया में गतिज ऊर्जा संरक्षित होती है ? यदि नहीं, तो इसमें परिवर्तन का स्रोत क्या है ?
View Solution10gm द्रव्यमान और 500 m/s चाल वाली बंदूक की गोली एक दरवाजे के ठीक केंद्र में टकराकर उसमें अंतः स्थापित हो जाती है । दरवाजा 1.0 m चौड़ा है और इसका द्रव्यमान 12 kg है । इसके एक सिरे पर कब्जे लगे हैं और यह इनमें गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है । गोली के दरवाजे में अंतः स्थापन के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए । ( संकेत - एक सिरे से गुजरती ऊर्ध्वाधर अक्ष के परितः दरवाजे का जड़त्व - आघूर्ण `ML^(2)//3` है )
View Solutionदो चक्रिकाएँ जिनके अपने - अपने अक्षों ( चलित के अभिलंबवत तथा चक्रिका के केंद्र से गुजरने वाले ) के परितः जड़त्व आघूर्ण `I_(1)` तथा `I_(2)` हैं और जो `omega_(1)` तथा `omega_(2)` कोणीय चालों में घूर्णन कर रही हैं , को उनके घूर्णन अक्ष संपाती करने सामने लाया जाता है । ( a ) इस दो चक्रिका निकाय की कोणीय चाल क्या है ? ( b ) यह दर्शाइए कि इस संयोजित निकाय की गतिज ऊर्जा दोनों चक्रिकाओं की आरंभिक गतिज ऊर्जाओं के योग से कम है । ऊर्जा में हुई इस हानि की आप कैसे व्याख्या करेंगे ? `omega_(1) ne omega_(2)` लीजिए |
View Solution( a ) लंबवत अक्षों के प्रमेय की उत्पत्ति करें । (संकेत : `(x,y)` ) तल के लंबवत मूलबिंदु से गुजरती अक्ष से किसी बिंदु `x-y` की दूरी का वर्ग `(x^(2) + y^(2))` है ।)
View Solution( b ) समांतर अक्षों के प्रमेय की उत्पत्ति करें ( संकेतः द्रव्यमान केंद्र को मूलबिंदु ले लिया जाय तो `Sigmam_(i)r_(i)=0.`)
View Solutionसूत्र `v^(2)=(2gh)/((1+K^(2)//R^(2)))` को गतिकीय दृष्टि ( अर्थात बलों तथा बल आघूर्णों के विचार ) से व्युत्पन्न कीजिए । जहाँ v लोटनिक गति करते पिंड ( वलय, डिस्क, बेलन या गोला ) का आनत तल की तली में वेग है । आनत तल पर h वह ऊँचाई है जहाँ से पिंड गति प्रारंभ करता है । k सममित अक्ष के परितः पिंड की घूर्णन त्रिज्या है और R पिंड की त्रिज्या है ।
View Solutionअपने अक्ष पर `omega_(0)` कोणीय चाल से घूर्णन करने वाली किसी चक्रिका को धीरे से ( स्थानांतरीय धक्का दिए बिना ) किसी पूर्णतः घर्षणरहित मेज पर रखा जाता है । चक्रिका की त्रिज्या r है । चित्र में दर्शाई चक्रिका के बिंदुओं A, B तथा C पर रैखिक वेग क्या हैं ? क्या यह चक्रिका चित्र में दर्शाई दिशा में लोटनिक गति करेगी ?
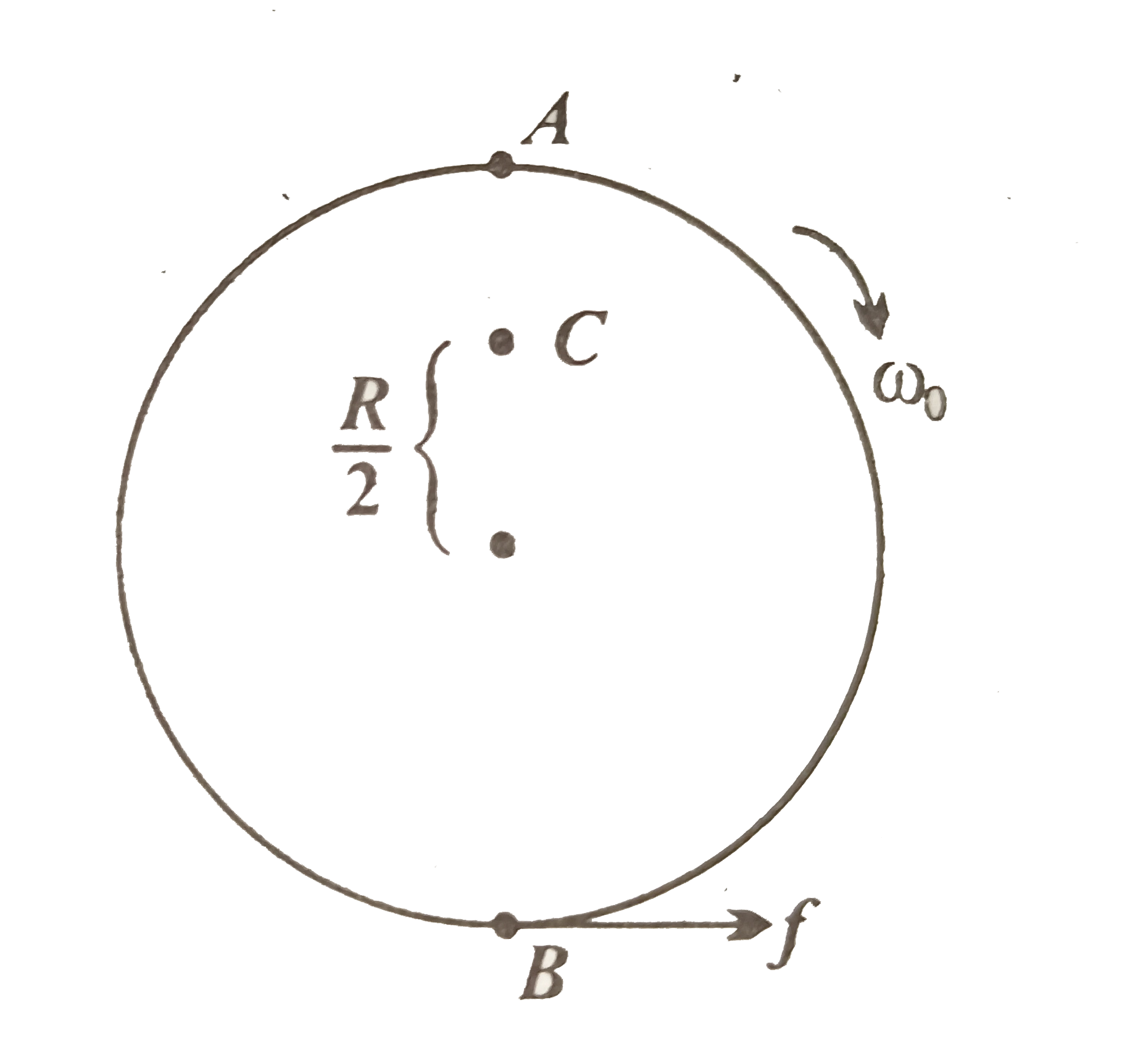
View Solutionस्पष्ट कीजिए कि चित्र ( प्रश्न 28 में दिए गए ) में अंकित दिशा में चक्रिका की लोटनिक गति के लिए घर्षण होना आवश्यक क्यों है ?
( a ) B पर घर्षण बल की दिशा तथा परिशुद्ध ( perfect ) लुढकन आरंभ होने से पूर्व घर्षण बल आघूर्ण की दिशा क्या है ?
View Solutionस्पष्ट कीजिए कि चित्र ( प्रश्न 28 में दिए गए ) में अंकित दिशा में चक्रिका की लोटनिक गति के लिए घर्षण होना आवश्यक क्यों है ?
( b ) परिशुद्ध लोटनिक गति आरंभ होने के पश्चात घर्षण बल क्या है ?
View Solution10 cm त्रिज्या की कोई ठोस चक्रिका तथा इतनी ही त्रिज्या का कोई छल्ला किसी क्षैतिज मेज पर एक ही क्षण `10xx" rads"^(-1)` की कोणीय चाल से रखे जाते हैं । इनमें से कौन पहले लोटनिक गति आरंभ कर देगा । गतिज घर्षण गुणांक `mu_(k)=0.2.`
View Solution10 kg द्रव्यमान तथा 15cm त्रिज्या का कोई सिलिंडर किसी `30^(@)` झुकाव के समतल पर परिशुद्धतः लोटनिक गति कर रहा है । स्थैतिक घर्षण गुणांक `mu_(s)=0.25` है ।
( a ) सिलिंडर पर कितना घर्षण बल कार्यरत है ?
View Solution10 kg द्रव्यमान तथा 15cm त्रिज्या का कोई सिलिंडर किसी `30^(@)` झुकाव के समतल पर परिशुद्धतः लोटनिक गति कर रहा है । स्थैतिक घर्षण गुणांक `mu_(s)=0.25` है ।
( b ) लोटन की अवधि में घर्षण के विरुद्ध कितना कार्य किया जाता है ? ।
View Solution10 kg द्रव्यमान तथा 15cm त्रिज्या का कोई सिलिंडर किसी `30^(@)` झुकाव के समतल पर परिशुद्धतः लोटनिक गति कर रहा है । स्थैतिक घर्षण गुणांक `mu_(s)=0.25` है ।
( c ) यदि समतल के झुकाव `theta` में वृद्धि कर दी जाए तो `theta` के किस मान पर सिलिंडर परिशुद्धतः लोटनिक गति करने की बजाय फिसलना आरंभ कर देगा ?
View Solutionनीचे दिए गए प्रत्येक प्रकथन को ध्यानपूर्वक पढ़िए तथा कारण सहित उत्तर दीजिए कि इनमें से कौन - सा सत्य है और कौन सा असत्य है ।
(a) लोटनिक गति करते समय घर्षण बल उसी दिशा में कार्यरत होता है जिस दिशा में पिंड का द्रव्यमान केंद्र गति करता है ।
View Solutionनीचे दिए गए प्रत्येक प्रकथन को ध्यानपूर्वक पढ़िए तथा कारण सहित उत्तर दीजिए कि इनमें से कौन - सा सत्य है और कौन सा असत्य है ।
(b) लोटनिक गति करते समय संपर्क बिंदु की तात्क्षणिक चाल शून्य होती है ।
View Solutionनीचे दिए गए प्रत्येक प्रकथन को ध्यानपूर्वक पढ़िए तथा कारण सहित उत्तर दीजिए कि इनमें से कौन - सा सत्य है और कौन सा असत्य है ।
(c) लोटनिक गति करते समय संपर्क बिंदु का तात्क्षणिक त्वरण शून्य होता है ।
View Solutionनीचे दिए गए प्रत्येक प्रकथन को ध्यानपूर्वक पढ़िए तथा कारण सहित उत्तर दीजिए कि इनमें से कौन - सा सत्य है और कौन सा असत्य है ।
( d ) परिशुद्ध लोटनिक गति के लिए घर्षण के विरुद्ध किया गया कार्य शून्य होता है ।
View Solutionनीचे दिए गए प्रत्येक प्रकथन को ध्यानपूर्वक पढ़िए तथा कारण सहित उत्तर दीजिए कि इनमें से कौन - सा सत्य है और कौन सा असत्य है ।
( e) किसी पूर्णतः घर्षणरहित आनत समतल पर नीचे की ओर गति करते पहिए की गति फिसलन गति ( लोटनिक गति नहीं ) होगी ।
View Solutionकणों के किसी निकाय की गति को इसके द्रव्यमान केंद्र की गति और द्रव्यमान केंद्र के पारित : गति में अलग - अलग विचार करके दर्शाइए कि-
(a) `vecp=vec(p'_(i))+M vecV,` जहाँ `vec(p_(i))` (`m_(i)` द्रव्यमान वाले ) `i` - वें कण का संवेग है, और `vec(p'_(i))=m_(i)vec(v'_(i))`| ध्यान दें कि `vec(v'_(i))` द्रव्यमान केंद्र के सापेक्ष `i`- वें कण का वेग है । द्रव्यमान केंद्र की परिभाषा का उपयोग करके यह भी सिद्ध कीजिए कि `Sigmavec(p'_(i))=0. `
View Solutionकणों के किसी निकाय की गति को इसके द्रव्यमान केंद्र की गति और द्रव्यमान केंद्र के पारित : गति में अलग - अलग करके विचार करना दर्शाइए कि-
(b) `K=K'+1//2MV^(2)`
K कणों के निकाय की कुल गतिज ऊर्जा, K' = निकाय की कुल गतिज ऊर्जा जबकि कणों को गतिज ऊर्जा द्रव्यमान केंद्र के सापेक्ष ली जाये | `MV^(2)//2` संपूर्ण निकाय के ( अर्थात निकाय के द्रव्यमान केंद्र के ) स्थानांतरण की गतिज ऊर्जा है ।
View Solutionकणों के किसी निकाय की गति को इसके द्रव्यमान केंद्र की गति और द्रव्यमान केंद्र के पारित : गति में अलग - अलग करके विचार करना दर्शाइए कि-
(c) `vecL=vecL'+vecRxxMvecV`
जहाँ `vecL'=Sigma vec(r'_(i))xx vec(p'_(i)),` द्रव्यमान केंद्र के पारित : निकाय का कोणीय संवेग है जिसकी गणना में वेग द्रव्यमान केंद्र के सापेक्ष मापे गए हैं । याद कीजिए - `vec(r'_(i))=vec(r_(i))-vecR` शेष सभी चिन्ह अध्याय में प्रयुक्त के विभिन्न राशियों के मानक चिन्ह हैं । ध्यान दें कि `vecL'` द्रव्यमान केंद्र के परितः निकाय का कोणीय संवेग एवं `vecRxxMvecV` इसके द्रव्यमान - केंद्र का कोणीय संवेग है ।
View Solutionकणों के किसी निकाय की गति को इसके द्रव्यमान केंद्र की गति और द्रव्यमान केंद्र के पारित : गति में अलग - अलग करके विचार करना दर्शाइए कि-
(d) `(dvecL')/(dt)=Sigmavec(r'_(i))xx(d vecp')/(dt)`
यह भी दर्शाइए कि `(dvecL')/(dt)=vec(tau'_("ext")`
( जहाँ `vec(tau'_(ext"))` द्रव्यमान केंद्र के परितः निकाय पर लगाने वाले सभी बाह्य बल आघूर्ण हैं । )
( संकेत - द्रव्यमान केंद्र की परिभाषा एवं न्यूटन के गति के तृतीय नियम का उपयोग कीजिए । यह मान लीजिए कि किन्हीं दो कणों के बीच के आतंरिक बल उनको मिलाने वाली रेखा के अनुदिश कार्य करते हैं ।)
View Solution
NCERT पाठ्यपुस्तक के प्रश्नोत्तर questions and complete solutions for chapter कणों के निकाय की गति और घुर्णो गति of NAVBODH PHYSICS (HINDI) of Class 11
All Exercises from NAVBODH PARIKSHA SAAR Class 11 PHYSICS कणों के निकाय की गति और घुर्णो गति
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर
- अभ्यासार्थ प्रश्न (अति लघु उत्तरीय प्रश्न/एक शब्द/एक वाक्य )
- अभ्यासार्थ प्रश्न (उचित संबंध जोड़िए - )
- अभ्यासार्थ प्रश्न (दीर्घ उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (मूल्य आधारित प्रश्न )
- अभ्यासार्थ प्रश्न (रिक्त स्थानों की पूर्ति कीजिए - )
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (वस्तुनिष्ठ प्रश्न ) (बहुविकल्पीय प्रश्न )
- अभ्यासार्थ प्रश्न (सत्य/असत्य लिखिए - )
- आंकिक उदाहरण
- आंकिक उदाहरण प्लस
- आंकिक प्रश्न
- उदाहरण
- तथ्यात्मक प्रश्न
- बहुविकल्पीय प्रश्न
- बोधात्मक प्रश्न
- बोधात्मक प्रश्न प्लस