Complete Solutions to अभ्यास of chapter सरल रेखा में गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | सरल रेखा में गति |
| NCERT HINDI | अभ्यास |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
निचे दिए गए गति के कौन से उदाहरणों में वस्तु को लगभग बिंदु वस्तु माना जा सकता है :
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी ।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर ।
(c) जमीन से टकरा कर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर ।
View Solutionदो बच्चे A व B अपने विधालय O से लौट कर अपने-अपने घर क्रमश: P तथा Q को जा रहे है | उनके स्थिति-समय (x-t) ग्राफ चित्र 3.19 में दिखाए गए है | निचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए :
(a) B/A की तुलना में A/B विद्यालय से निकट रहता है ।
(b) B/A की तुलना में A/B विद्यालय से पहले चलता है ।
(c) B/A की तुलना A/B तेज चलता है ।
(d) A और B घर (एक ही/भिन्न) समय पर पहुँचते हैं ।
(e) A/B सड़क पर B/A से (एक बार/दो बार) आगे हो जाते हैं ।

View Solutionएक महिला अपने घर से प्रात: 9.00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर `5 km h^(-1)` चाल से चलती है | वहाँ वह सायं 5.00 बजे तक रहती है और `25 km h^(-1)` की चाल से चाल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है | उपयुक्त पैमाना चुनिए तथा उसकी गति का x-t ग्राफ खींचिए |
View Solutionकोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है | उसका हर कदम 1 m लंबा है और 1 s समय लगता है | उसकी गति का x-t ग्राफ खींचिए | ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहां से चलना प्रारंभ करता है वहाँ से 13 m दूर किसी गढ्डे में कितने समय पश्चात गिरता है |
View Solutionकोई जेट वायुयान `500 km h^(-1)` की चाल से चल रहा है ओर यह जेट यान के सापेक्ष `1500km h^(-1)` की चाल से अपने दहन उत्पादों को बाहर निकलता है । जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इस दहन उत्पादों की चाल क्या होगी ?
View Solutionसीधे राजमार्ग पर कोई कार `126 km h^(-1)` कि चाल से चल रही है | इसे 200 m कि दुरी पर रोक दिया जाता है | कार के मंदन को एकसमान मानिए और इसका मन निकालिए | कार को रुकने में कितना समय लगा ?
View Solutionदो रेलगाड़ियाँ A व B दो समांतर पटरियों पर `72 km h^(-1)` कि एकसमान चाल से एक ही दिशा में चल रही है | प्रत्येक गाड़ी 400 m लंबी है और गाड़ी A गाड़ी B से आगे है |B का चालक A से आगे निकलना चाहता है | तथा `1 m s^(-2)` से इसे त्वरित करता है | यदि 50 s के बाद B का गार्ड A के चालक से आगे हो जाता है तो दोनों के बिच आरंभिक दुरी कितनी थी ?
View Solutionदो-लेन वाली किसी सड़क पर कार A `36 km h^(-1)` की चाल से चल रही है | एक दूसरे की विपरीत दिशाओं में चलती दो कारें B व C जिनमें से प्रत्येक की चाल `54 km h^(-1)` है, कार A तक पहुंचना चाहती है | किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों 1 km है, कार का चालक यह निर्णय करता है कि कार C के कार A तक पहुंचने के पहले ही वह कार A से आगे निकल जाए | किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है ?
View Solutionदो नगर A व B नियमित बस सेवा द्वारा एक दूसरे से जुड़े हैं और प्रत्येक T मिनट के बाद दोनों तरफ से चलती है | कोई व्यक्ति साइकिल से `20 km h^(-1)`की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है | बस सेवाकाल T कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती है ?
View Solutionकोई खिलाड़ी एक गेंद को ऊपर की और आरम्भिक चाल `29 ms^(-1)` से फेंकता है,
(i) गेंद की ऊपर की और गति के दौरान त्वरण की दिशा क्या होगी ?
(ii) इसकी गति के उच्चतम बिन्दु पर गेंद के वेग व त्वरण क्या होंगे ?
(iii) गेंद के उच्चतम बिन्दु पर स्थान व समय `x=0` को `t=0` व चुनिए , ऊर्ध्वाधर नीचे की ओर की दिशा को अक्ष की धनात्मक दिशा मानिए । गेंद की तरफ की ऊपर व नीचे की ओर गति के दौरान स्थिति , वेग व त्वरण के चिन्ह बताइए ।
(iv) किस ऊँचाई तक गेंद ऊपर जाती है ओर कितनी देर के बाद गेंद खिलाड़ी के हाथो में आ जाती है ? [ `g = 9.8 ms^(-2)` तथा वायु का प्रतिरोध नगण्य है ।]
View Solutionनीचे दिए गए कथनों को ध्यान से पढ़िए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य है या असत्य, एकविमीय गति में किसी कण कि
(a) किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है |
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है |
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए |
(d) चाल अवश्य ही बढ़ती रहेगी, यदि उसका त्वरण धनात्मक हो |
View Solutionकिसी गेंद को 90 मीटर की ऊँचाई से फर्श पर गिराया जाता है फर्श के साथ प्रत्येक टक्कर में गेंद की चाल 1/10 कम हो जाती है इसकी गति का `t=0` से 12 सेकण्ड के बीच चाल - समय ग्राफ खींचिए ।
View Solutionउदाहरण सहित निम्नलिखित के बीच के अंतर को स्पष्ट कीजिए :
(a) किसी समय अंतराल में विस्थापन के परिमाण (जैसे कभी-कभी दूरी भी कहा जाता है) और किसी कण द्वारा उसी अंतराल के दौरान तय किए गए पथ की कुल लंबाई |
(b) किसी समय अंतराल में औसत वेग के परिमाण और उसी अंतराल में औसत चाल (किसी समय अंतराल में किसी कण की औसत चाल को समय अंतराल द्वारा विभाजित की गई कुल पथ-लंबाई के रूप में परिभाषित किया जाता है) प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि पहली से अधिक या उसके बराबर है | समता का चिन्ह कब सत्य होता है ? (सरलता के लिए केवल एकविमीय गति पर विचार कीजिए |)
View Solutionकोई व्यक्ति अपने घर से सीधी सड़क पर `5 km h^(-1)` की चाल से 2.5 km दूर बाजार तक पैदल चलता है |परंतु बाजार बंद देखकर वह उसी क्षण वापस मुड़ जाता है तथा `7.5 km h^(-1)` की चाल से घर लौट आता है | समय अंतराल (i) 0-30 मिनट, (ii) 0-50 मिनट, (iii) 0-40 मिनट की अवधि में उस व्यक्ति (a) के मध्य वेग का परिमाण, तथा (b) का मध्य चाल क्या है ? (नोट : आप इस उदाहरण के समय समझ सकेंगे की औसत चाल को औसत-वेग के परिमाण के रूप में परिभाषित करने की अपेक्षा समय द्वारा विभाजित कुल पथ-लंबाई के रूप में परिभाषित करना अधिक अच्छा क्यों है | आप थक कर घर लौट उस व्यक्ति को यह बताना नहीं चाहेंगे कि उसकी औसत चाल शून्य थी |)
View Solutionहमने अभ्यास 3.13 तथा 3.14 में औसत चाल व औसत वेग के परिमाण के बीच के अंतर को स्पष्ट किया है | यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का अंतर करना आवश्यक नहीं होता | तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है | क्यों ?
View Solutionचित्र 3.20 में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें कौन-सा ग्राफ एकविमीय गति को संभवत : नहीं दर्शा सकता |

View Solutionचित्र 3.21 में किसी कण की एकविमीय गति का x-t ग्राफ दिखाया गया है | ग्राफ से क्या यह कहना ठीक होगा कि यह कण `tlt0` के लिए किसी सरल रेखा में और `tgt0` के लिए किसी परवलीय पथ में गति करता है | यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक संदर्भ का सुझाव दीजिए |

View Solutionकिसी राजमार्ग पर पुलिस की कोई गाड़ी 30 km/h की चाल से चल रही है और यह उसी दिशा में 192 km/h की चाल से जा रही है किसी चोर की कार पर गोली चलाती है | यदि गोली की नाल मुखी चाल `150 m s^(-1)` है तो चोर की कार को गोली किस चाल के साथ अघात करेगी ? (नोट : उस चाल को ज्ञात कीजिए जो चोर की कार को हानि पहुंचाने में प्रासंगिक हो) |
View Solutionचित्र 3.22 में दिखाए गए प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए :

View Solutionचित्र 3.23 में किसी कण की एकविमीय सरल आवर्ती गति के लिए x-t ग्राफ दिखाया गया है | (इस गति के बारे में आप अध्याय 14 में पढ़ेंगे) समय t=0.3 s, -1.2 s पर कण के स्थिति, बेग व त्वरण के चिन्ह क्या होंगे ?

View Solutionचित्र 3.24 किसी कण की एकविमीय गति का x-t ग्राफ दर्शाता है | इसमें तीन सामान अंतराल दिखाया गए है | किस अंतराल में औसत चाल अधिकतम है और किसमें न्यूनतम है ? प्रत्येक अंतराल के लिए औसत वेग का चिन्ह बताइए |
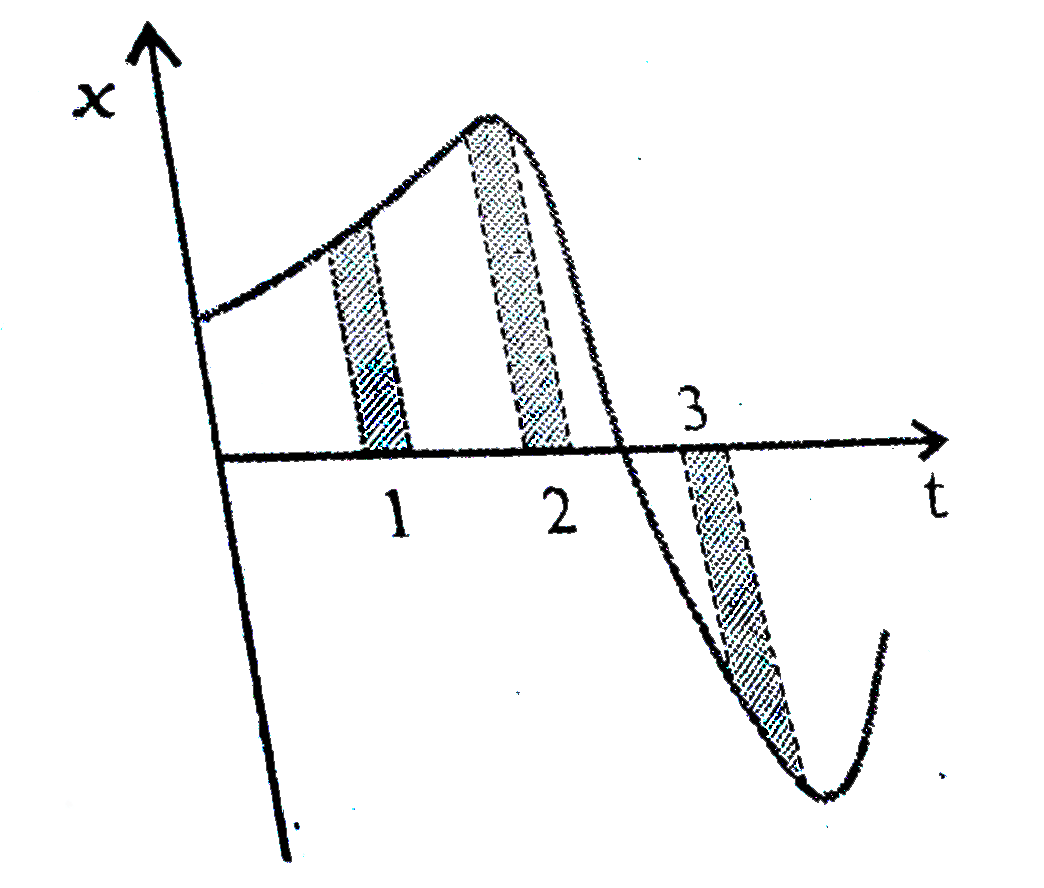
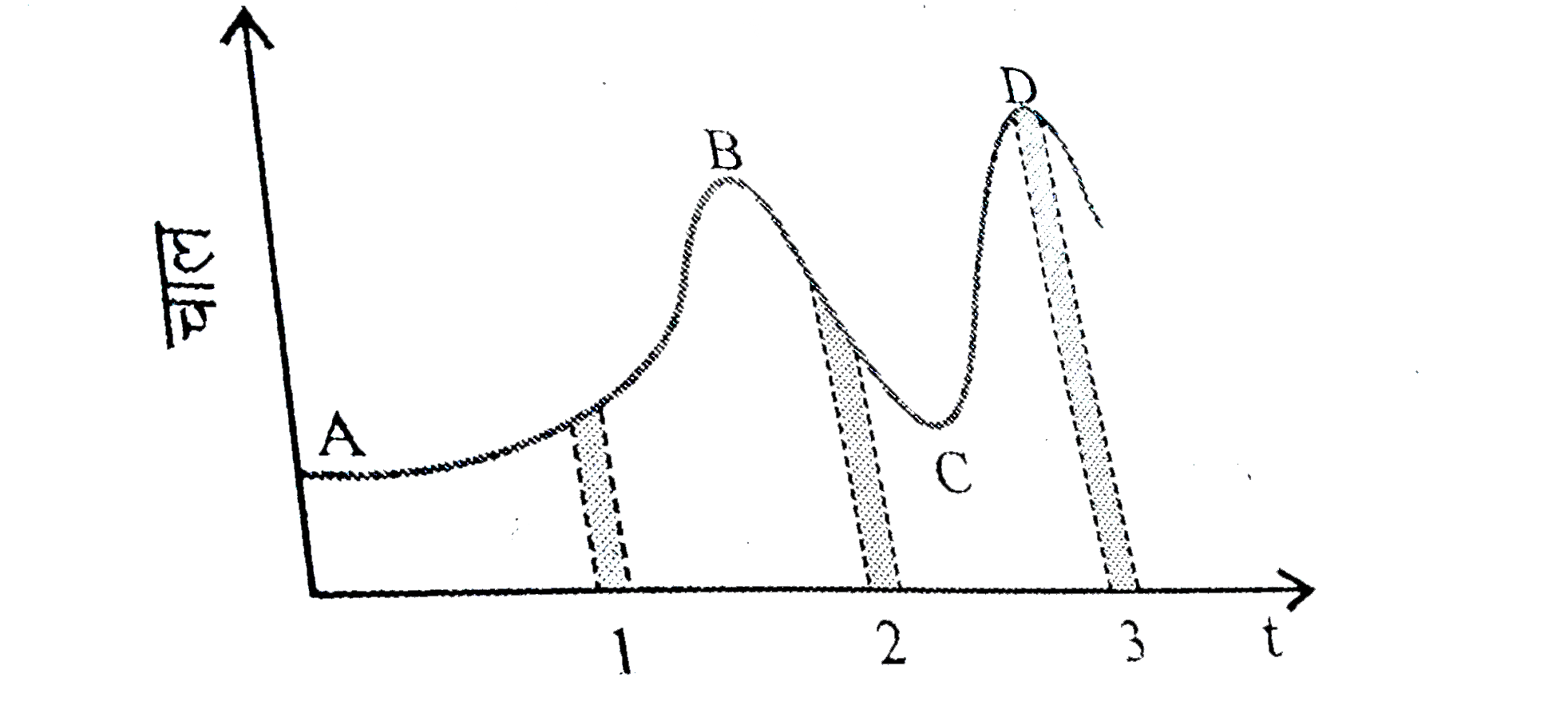
View Solutionचित्र 3.25 में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण का चाल-समय ग्राफ दिखाया गया है | इसमें तीन समान समय अंतराल दिखाए गए हैं | किस अंतराल में औसत त्वरण का परिमाण अधिकतम होगा ? किस अंतराल में औसत चाल अधिकतम होगी ? धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अंतरालों v में तथा a के चिन्ह बताइए | A, B, C, व D बिंदुओं पर त्वरण क्या होंगे ?
View Solutionकोई तीन पहिए वाली स्कूटर अपनी विरामावस्था से गति प्रारंभ करता है | फिर 10 s तक किसी सीधी सड़क पर `1 m s^(-2)` के एकसमान त्वरण से चलता है | इसके बाद वह एकसमान वेग से चलता है | स्कूटर द्वारा n वे सेकेंड `(n=1,2,3.......)` में तय की गई दूरी को n के सापेक्ष आलेखित कीजिए | आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा ?
View Solutionकिसी स्थिर लिफ्ट में (जो ऊपर से खुली है) कोई बालक खड़ा है | वह अपने पूरे जोर से एक गेंद ऊपर की ओर फेंकता है जिसका प्रारंभिक चाल `49 m s^(-1)` है | उसके हाथों में गेंद के वापिस आने में कितना समय लगेगा ? यदि लिफ्ट ऊपर की ओर `5 m s^(-1)` एकसमान चाल से गति पर करना प्रारंभ कर दें और वह बालक फिर गेंद को अपने पूरे जोर से फेकता तो कितनी देर में गेंद उसके हाथों में लौट आएगी ?
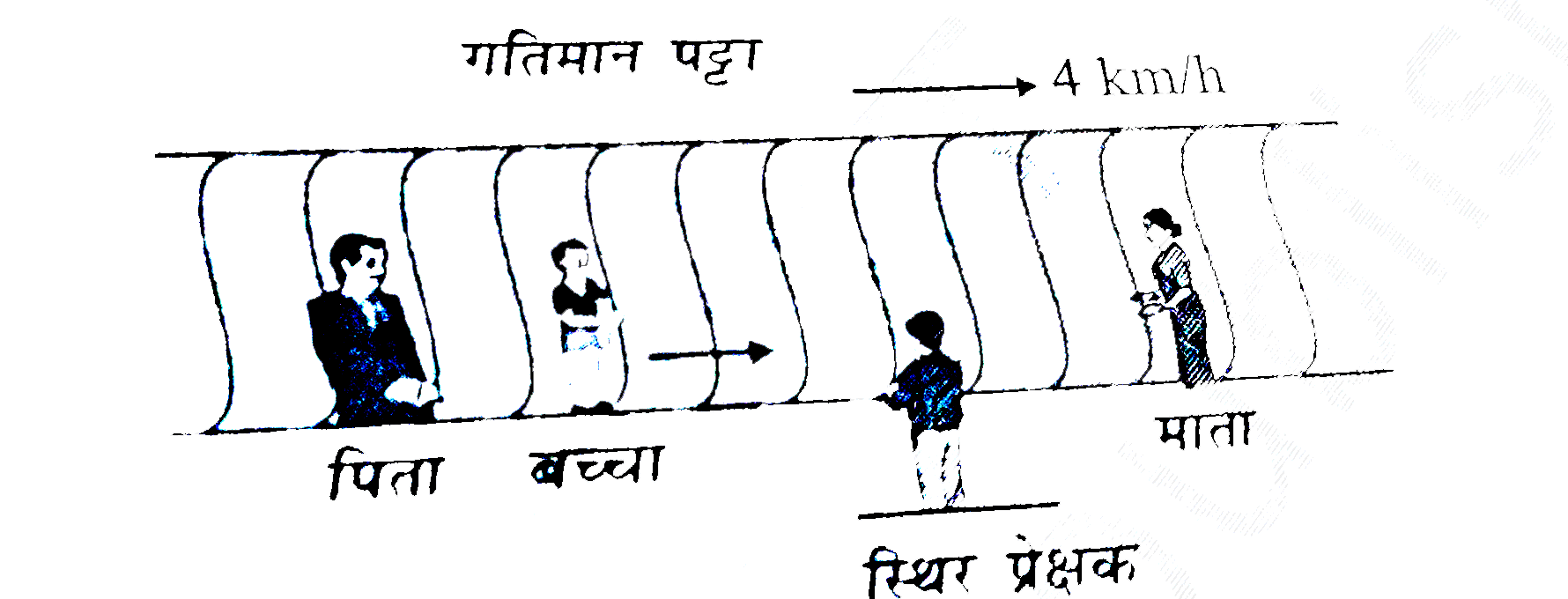
View Solutionक्षैतिज में गतिमान कोई लंबा पट्टा (चित्र 3.26) 4 km/h की चाल से चल रहा है | एक बालक इस पर (पट्टे के सापेक्ष) 9 km/h की चाल से कभी आगे कभी पीछे अपने माता-पिता के बीच दौड़ रहा है | माता व पिता के बीच 50 m की दूरी है | बाहर की किसी स्थिर प्लेटफार्म पर खड़े एक प्रेक्षक के लिए, निम्नलिखित का मान प्राप्त करिए |
(a) पट्टे की गति की दिशा में दौड़ रहे बालक की चाल,
(b) पट्टे की गति की दिशा में विपरीत दौड़ रहे बालक की चाल,
(c) बच्चे द्वारा (a) व (b) में लिया गया समय यदि बालक की गति का प्रेक्षण उसके माता या पिता करे तो कौन-सा उत्तर बदल जाएगा ?
View Solutionकिसी 200 m ऊंची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर `15 m s^(-1)` तथा `30 m s^(-1)` की प्रारंभिक चाल से फेंका जाता है | इसका सत्यापन कीजिए कि नीचे दिखाया गया ग्राफ (चित्र 3.27) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है | वायु के प्रतिरोध को नगण्य मानिए और यह मानीय की जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं | मान लीजिए `g=10 m s^(-2)` | ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए |
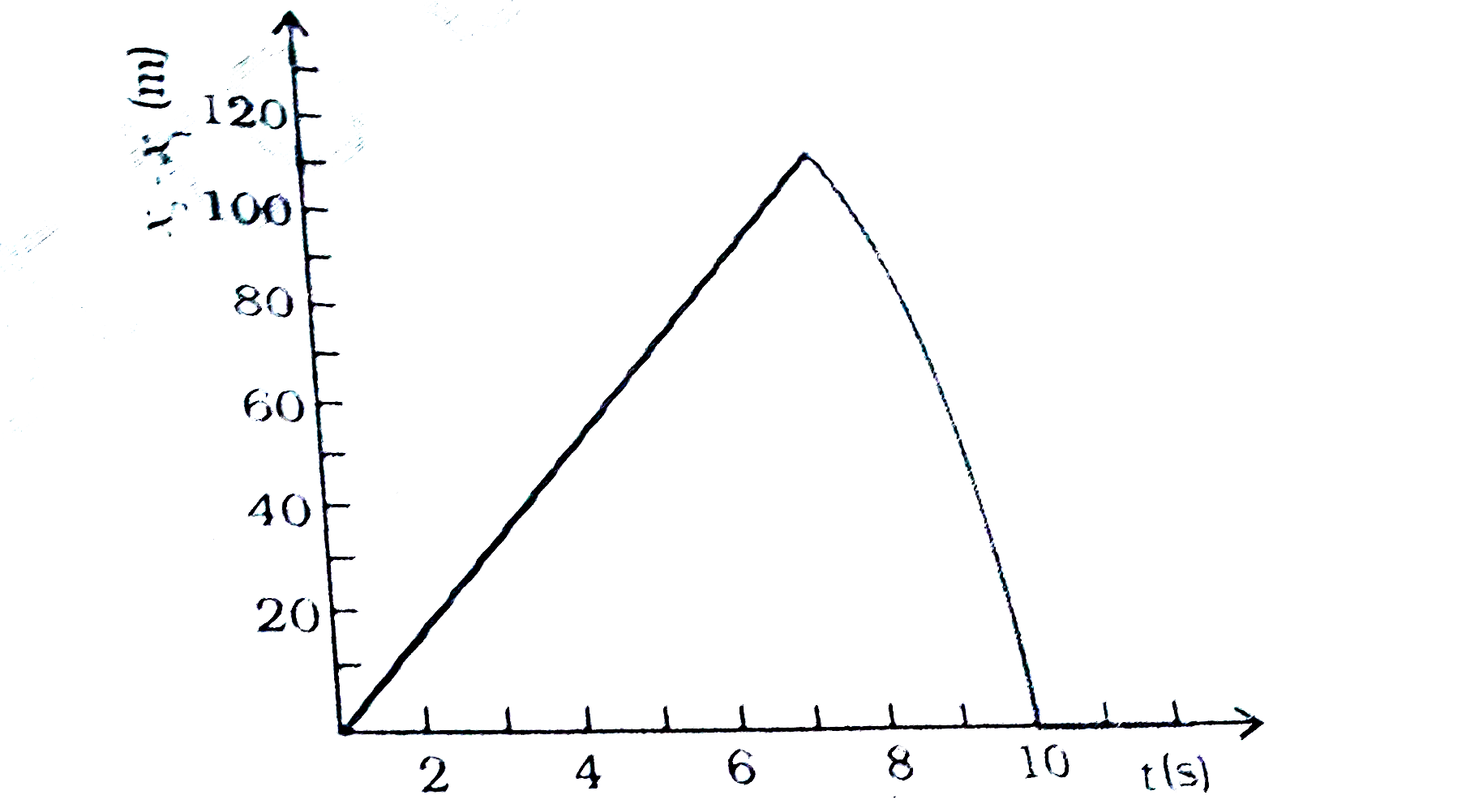
View Solutionकिसी निश्चित दिशा के अनुदिश चल रहे किसी कण का चाल-समय ग्राफ चित्र 3.28 में दिखाया गया है | कण द्वारा (a) t=0 s से t=10 s, (b) t=2 s से 6s के बीच तय की गई दूरी ज्ञात कीजिए |
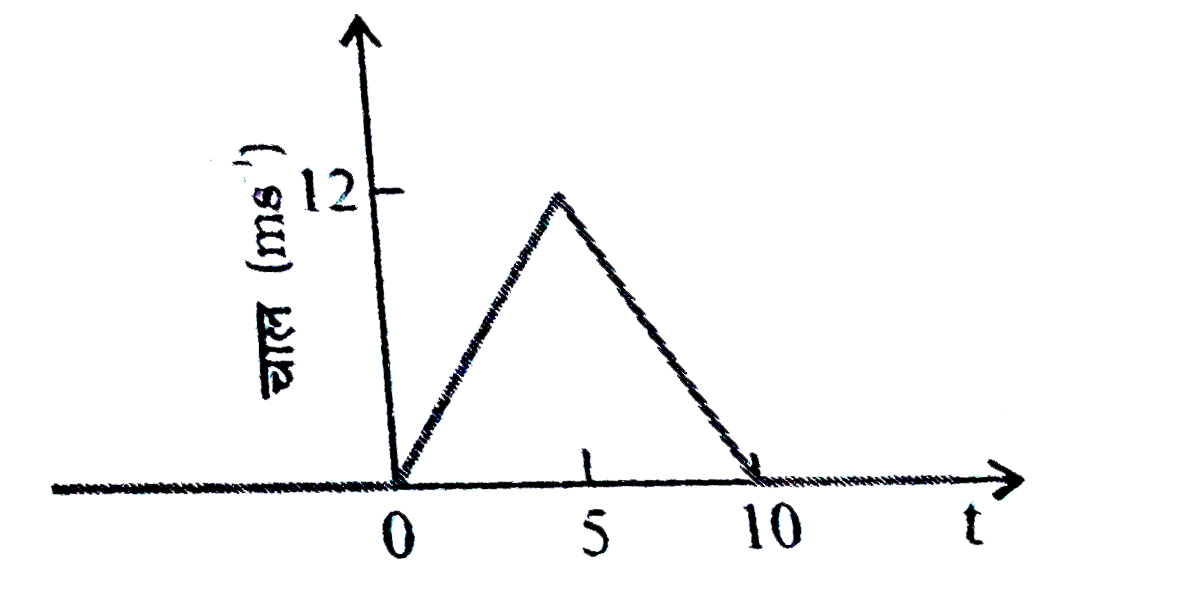
(a) तथा (b) में दिए गए अंतरालों की अवधि में कण की औसत चाल क्या है ?
View Solutionएकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र 3.29 में दिखाया गया है :

नीचे दिए सूत्रों में `t_(1)` से `t_(2)` तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-सा सूत्र सही है :
(i) `x(t_(2))=x(t_(1))+v(t_(1))(t_(2)-t_(1))+(1//2)a(t_(2)-t_(1))^(2)`
(ii) `v(t_(2))=v(t_(1))+a(t_(2)-t_(1))`
(iii) `v_("average")=[x(t_(2))-x(t_(1))]//(t_(2)-t_(1))`
(iv) `a_("average")=[v(t_(2))-v(t_(1))]//(t_(2)-t_(1))`
(v) `x(t_(2))=x(t_(1))+v_("average")(t_(2)-t_(1))+(1//2)a_("average")(t_(2)-t_(1))^(2)`
(vi) `x(t_(2))-x(t_(1))=t`-अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |
View Solution
अभ्यास questions and complete solutions for chapter सरल रेखा में गति of NCERT भौतिकी(HINDI) of Class 11