Complete Solutions to SOLVED EXAMPLES of chapter STRAIGHT LINES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | STRAIGHT LINES |
| Mathematics | SOLVED EXAMPLES |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Find the distance between the parallel lines `3x 4y + 7 = 0`and`3x 4y + 5 = 0`.
View SolutionFind the distance of the point `(3, - 5)`from the line `3x - 4y - 26 =0`.
View SolutionFind the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with the positive direction of x–axis is 15°.
View SolutionFind the equation of the line, which makes intercepts `3` and 2 on the x and y axes respectively.
View SolutionEquation of a line is `3x-4y+10=0`. Find its (i) slope, (ii) x and yintercepts.
View SolutionThe Fahrenheit temperature F and absolute temperature K satisfy a linear equation. Given that `K = 273`when `F = 32`and that `K = 373`when`F = 212`. Express K in terms of F and find the value of F, when `K = 0`.
View SolutionFind the angle between the lines `y-sqrt(3)x-5=0`and `sqrt(3)y-x+6=0`.
View SolutionReduce the equation `sqrt(3)x+y-8=0` into normal form. Find the values of p and `omega`.
View SolutionFind the equation of a line perpendicular to the line `x-2y+3=0`and passing through the point `(1, 2)`.
View SolutionShow that two lines `a_1x+b_1y+c_1=0`and `a_2x+b_2y+c_2=0`, where `b_1,b_2!=0`are :
(i) Parallel if `(a_1)/(b_1)=(a_2)/(b_2),`and (ii) perpendicular if `a_1a_2+b_1b_2=0`.
View SolutionIf the lines `2a + y 3 = 0`, `5x + k y 3 = 0`and `3x y 2 = 0`are concurrent, find the value of k.
View SolutionFind the distance of the line `4x y = 0` from the point `P(4, 1)` measured along the line making an angle of `135^0`with the positive x-axis.
View SolutionAssuming that straight lines work as the plane mirror for a point, find the image of the point (1, 2) in the line `x - 3y + 4 = 0`.
View SolutionShow that the area of the triangle formed by the lines `y=m_1x+c_1,y=m_2x+c_2`and `x=0` is `((c_2-c_1)^2)/(2|m_1-m_2|)`
View SolutionA line is such that its segment between the lines `5x-y + 4 = 0`and `3x + 4y -4 = 0` is bisected at the point (1, 5). Obtain its equation.
View SolutionShow that the path of a moving point such that its distances from two lines `3x -2y = 5`and `3x + 2y = 5`are equal is a straight line.
View SolutionWrite the equation of the line through the points `(1, 1)`and `(3, 5)`.
View SolutionWrite the equation of the line for which `tantheta=1/2,`where `theta`is the inclination of the line and
(i) yintercept is `-3/2`
(ii) xintercept is 4.
View SolutionFind the equations of the lines parallel to axes and passing through`(-2, 3)`.
View SolutionFind the equation of the line through `( 2, 3)`with slope ` 4`.
View SolutionThree points `P(h ,k),Q(x_1,y_1)`and `R(x_2,y_2)`lie on a line. Show that `(h-x_1)(y_2-y_1)=(k-y_1)(x_2-x_1)`.
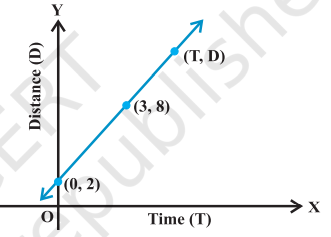
View SolutionIn Figure, time and distance graph of a linear motion is given. Two positions of time and distance are recorded as, when T = 0, D = 2 and when T = 3, D = 8. Using die concept of slope, find law of motion, i.e., how distance depends upon time.
View SolutionIf the angle between two lines is `pi/4`and slope of one of the lines is `1/2`, find the slope of the other line.
View SolutionLine through the points `(-2, 6)`and `(4, 8)`is perpendicular to the line through the points `(8, 12)`and `(x , 24)`. Find the value of x.
View SolutionFind the slope of the lines:
(a) Passing through the points `(3, -2)`and `( -1,4)`,
(b) Passing through the points `(3, -2)`and `(7, -2)`,
(c) Passing through the points `(3,-2)`and `(3,4)`,
(d) Making inclination of `60^@`with the positive direction of x-axis.
View SolutionFind the equation of line parallel to the y-axis and drawn through the point of intersection of `x \ 7y+\ 5\ =\ 0`and `3x+y \ 7\ =\ 0`.
View SolutionFind the new coordinates of point `(3,4)` if the origin is shifted to (1, 2) by a translation.
View SolutionFind the transformed equation of the straight line `2x - 3y+ 5= 0`, when the origin is shifted to the point `(3, -1)` after translation of axes.
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter STRAIGHT LINES of NCERT MATHEMATICS(HINGLISH) of Class 11