Complete Solutions to Exercise of chapter સંબંધ અને વિધેયો of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | સંબંધ અને વિધેયો |
| NCERT | Exercise |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
જો `(x/3 +1, y -2/3) = (5/3, 1/3)` તો `x` અને `y` શોધો.
View Solutionજો ગણ `A` માં `3` ઘટકો હોય અને ગણ `B = {3, 4, 5},` તો `(A xx B)` ના ઘટકોની સંખ્યા શોધો.
View Solutionજો `G = {7, 8}` અને `H = {5, 4, 2},` તો `G xx H` અને `H xx G` શોધો.
View Solutionનીચે આપેલાં વિધાનોમાંથી કયું વિધાન સત્ય છે અને કયું વિધાન અસત્ય છે તે જણાવો તથા અસત્ય વિધાન સત્ય બને તે રીતે ફરી લખો : જો `P = {m, n}` અને `Q = { n, m},` તો `P xx Q = {m, n),(n, m)}`.
View Solutionનીચે આપેલાં વિધાનોમાંથી કયું વિધાન સત્ય છે અને કયું વિધાન અસત્ય છે તે જણાવો તથા અસત્ય વિધાન સત્ય બને તે રીતે ફરી લખો : જો A અને B અરિક્ત ગણો હોય, તો જ્યાં `x ∈ A` તથા `y ∈ B` હોય તેવી તમામ ક્રમયુક્ત જોડો `(x, y)` થી બનતો અરિક્ત ગણ `A xx B` છે.
View Solutionનીચે આપેલાં વિધાનોમાંથી કયું વિધાન સત્ય છે અને કયું વિધાન અસત્ય છે તે જણાવો તથા અસત્ય વિધાન સત્ય બને તે રીતે ફરી લખો : જો `A = {1, 2}, B = {3, 4},` તો `A xx (B cap phi ) = phi`.
View Solutionજો `A = {-1, 1},` તો `A xx A xx A` મેળવો.
View Solutionજો `A xx B = {(a, x),(a , y), (b, x), (b, y)}`, તો `A` અને `B` શોધો.
View Solutionધારો કે `A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6}` અને `D = {5, 6, 7, 8},` તો નીચેનાં પરિણામો ચકાસો : `A xx (B cap C) = (A xx B) cap (A xx C)`
View Solutionધારો કે `A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6}` અને `D = {5, 6, 7, 8},` તો નીચેનાં પરિણામો ચકાસો : `A xx C` એ `B xx D` નો ઉપગણ છે.
View Solutionજો `A = {1, 2}` અને `B = {3, 4}` તો `A xx B` લખો. `A xx B` ને કેટલા ઉપગણો હશે ? તે તમામ ઉપગણોની યાદી બનાવો.
View Solutionજો `n(A) =3` અને `n(B) = 2` હોય તેવા બે ગણો `A` અને `B` હોય અને ભિન્ન ઘટકો `x, y` અને `z` માટે `(x, 1), (y, 2), (z, 1)` એ `A xx B` ના ઘટકો હોય તો `A` અને `B` શોધો.
View Solutionજો કાર્તેઝિય ગુણાકાર `A xx A` ના ઘટકોની સંખ્યા `9` હોય અને તેમાંના બે ઘટકો `(-1, 0)` અને `(0,1)` હોય, તો `A` શોધો તથા `A xx A` ના બાકીના ઘટકો લખો.
View Solution`A = {1, 2, 3,...,14). R= {(x, y) :` `3x -y = 0`, જ્યાં `x, y ∈ A}`. જો `R` એ `A` થી `A` નો સંબંધ હોય, તો `R` નો પ્રદેશ, સહપ્રદેશ અને વિસ્તાર મેળવો.
View Solution`A = {(x, y) : y = x + 5, x` એ `4` થી નાની પ્રાકૃતિક સંખ્યા છે, `x, y ∈ N`} થાય તે રીતે એક સંબંધ `N` પર વ્યાખ્યાયિત છે. `R` ને યાદીની રીતે લખો. `R` નો પ્રદેશ તેમજ વિસ્તાર મેળવો.
View Solution`A = {1, 2, 3, 5}` અને `B = {4, 6, 9}. R = {(x, y): x ` અને `y` નો તફાવત અયુગ્મ સંખ્યા છે, `x ∈ A`, `y ∈ B`} થાય તે રીતે સંબંધ `A` થી `B` પર વ્યાખ્યાયિત છે. `R` ને યાદીની રીતે લખો.
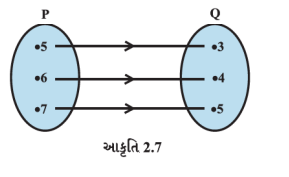
View Solutionઆકૃતિ 2.7 માં `P` થી `Q` નો સંબંધ દર્શાવેલ છે. આ સંબંધને ગુણધર્મની રીતે.
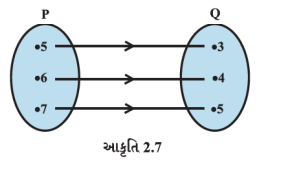
View Solutionઆકૃતિ 2.7 માં `P` થી `Q` નો સંબંધ દર્શાવેલ છે. આ સંબંધને યાદીની રીતે લખો. તેનો પ્રદેશ અને વિસ્તાર શું થશે ?
View Solutionજો `A = {1, 2, 3, 4, 6}.` `R={(a, b): a, b ∈ A, b` એ `a` વડે વિભાજ્ય છે.} થાય તે રીતે સંબંધ `R` એ `A` પર વ્યાખ્યાયિત છે, (i) `R` ને યાદીની રીતે લખો.
View Solutionજો `A = {1, 2, 3, 4, 6}.` `R={(a, b): a, b ∈ A, b` એ `a` વડે વિભાજ્ય છે.} થાય તે રીતે સંબંધ `R` એ `A` પર વ્યાખ્યાયિત છે, (ii) `R` નો પ્રદેશ મેળવો.
View Solutionજો `A = {1, 2, 3, 4, 6}.` `R={(a, b): a, b ∈ A, b` એ `a` વડે વિભાજ્ય છે.} થાય તે રીતે સંબંધ `R` એ `A` પર વ્યાખ્યાયિત છે, (iii) `R` નો વિસ્તાર મેળવો.
View Solution`R= {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}` થાય તે રીતે વ્યાખ્યાયિત સંબંધનો પ્રદેશ તેમજ વિસ્તાર મેળવો.
View Solutionસંબંધ `R = {(x, x^(3)) :x` એ `10` કરતાં નાની અવિભાજ્ય સંખ્યા છે} ને યાદીના સ્વરૂપમાં લખો.
View Solutionજો `A = {x, y, z}` અને `B = {1, 2}` તો `A` થી `B` ના સંબંધોની સંખ્યા શોધો.
View Solution`R` એ `Z` પર `R = {(a,b): a, b ∈ Z`, `a - b` એ પૂર્ણાક છે.} દ્વારા વ્યાખ્યાયિત છે. `R` નો પ્રદેશ અને વિસ્તાર મેળવો.
View Solutionનીચેના પૈકી કયો સંબંધ વિધેય છે? કારણ આપો. જો તે વિધેય હોય, તો તેનો પ્રદેશ અને વિસ્તાર શોધો. {(2,1), (5, 1), (81), (11,1), (141), (17,1)}
View Solutionનીચેના પૈકી કયો સંબંધ વિધેય છે? કારણ આપો. જો તે વિધેય હોય, તો તેનો પ્રદેશ અને વિસ્તાર શોધો. `{(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)} `
View Solutionનીચેના પૈકી કયો સંબંધ વિધેય છે? કારણ આપો. જો તે વિધેય હોય, તો તેનો પ્રદેશ અને વિસ્તાર શોધો. {(1,3), (1,5), (2,5)}
View Solutionનીચેના વાસ્તવિક વિધેયના પ્રદેશ અને વિસ્તાર શોધો : `f(x) = -|x|`
View Solutionનીચેના વાસ્તવિક વિધેયના પ્રદેશ અને વિસ્તાર શોધો : `f(x) = sqrt(9 - x^(2))`
View Solution`f(x)= 2x -5` થી વ્યાખ્યાયિત વિધેય માટે નીચેની કિંમતો શોધો : f (0)
View Solution`f(x)= 2x -5` થી વ્યાખ્યાયિત વિધેય માટે નીચેની કિંમતો શોધો : f(7)
View Solution`f(x)= 2x -5` થી વ્યાખ્યાયિત વિધેય માટે નીચેની કિંમતો શોધો : f(-3)
View Solutionવિધેય `t` એ સેલ્સિયસમાં ઉષ્ણતામાન અને ફેરનહીટમાં ઉષ્ણતામાન વચ્ચે રૂપાંતર કરતું સૂત્ર `t(C) = (9C)/5 + 32` દ્વારા વ્યાખ્યાયિત હોય, તો નીચેનાં મૂલ્યો શોધો : `t(0)`
View Solutionવિધેય `t` એ સેલ્સિયસમાં ઉષ્ણતામાન અને ફેરનહીટમાં ઉષ્ણતામાન વચ્ચે રૂપાંતર કરતું સૂત્ર `t(C) = (9C)/5 + 32` દ્વારા વ્યાખ્યાયિત હોય, તો નીચેનાં મૂલ્યો શોધો : `t(28)`
View Solutionવિધેય `t` એ સેલ્સિયસમાં ઉષ્ણતામાન અને ફેરનહીટમાં ઉષ્ણતામાન વચ્ચે રૂપાંતર કરતું સૂત્ર `t(C) = (9C)/5 + 32` દ્વારા વ્યાખ્યાયિત હોય, તો નીચેનાં મૂલ્યો શોધો : `t(-10)`
View Solutionવિધેય `t` એ સેલ્સિયસમાં ઉષ્ણતામાન અને ફેરનહીટમાં ઉષ્ણતામાન વચ્ચે રૂપાંતર કરતું સૂત્ર `t(C) = (9C)/5 + 32` દ્વારા વ્યાખ્યાયિત હોય, તો નીચેનાં મૂલ્યો શોધો : જો `t(C)= 212` હોય, તો C શોધો.
View Solutionનીચેના વિધેયોના વિસ્તાર શોધો : `f (x) = 2 -3x`, `x ∈ R`, `x gt 0`
View Solutionનીચેના વિધેયોના વિસ્તાર શોધો : `f (x) = x^(2) + 2, x` વાસ્તવિક સંખ્યા છે.
View Solutionનીચેના વિધેયોના વિસ્તાર શોધો : `f(x) = x, x` વાસ્તવિક સંખ્યા છે.
View Solutionજો `f (x) = x^(2)`, તો `(f(1.1) - f(1))/(1.1 -1)` શોધો
View Solutionવિધેય `f(x) = (x^(2)+x+1)/(x^(2) -8x+12)` નો પ્રદેશ શોધો.
View Solution`f (x) = sqrt(x-1)` થી વ્યાખ્યાયિત વાસ્તવિક વિધેય f નો પ્રદેશ અને વિસ્તાર શોધો.
View Solution`f (x) = |x-1|` થી વ્યાખ્યાયિત વાસ્તવિક વિધેય f નો પ્રદેશ અને વિસ્તાર શોધો.
View Solutionજો `f = {(x, x^(2)/(1+x^(2))) : x ∈ R}` એ R થી Rનું વિધેય હોય, તો તે વિધેય f નો વિસ્તાર શોધો.
View Solution`f, g : R rarr R, f(x) =x + 1,g(x) = 2x -3` થી વ્યાખ્યાયિત વિધેય છે, તો `f+g , f-g` અને `f/g` શોધો.
View Solutionજો `f = {(1, 1), (2, 3), (0,-1), (-1, -3)}` એ `f(x) = ax + b`, થી વ્યાખ્યાયિત સંબંધ હોય, તો `a` અને `b` શોધો.
View Solution`R` એ `N` થી નો સંબંધ છે. `R = {(a, b) : a, b ∈ N` અને `a = b^(2)`} થાય તે રીતે વ્યાખ્યાયિત છે, તો શું નીચેનાં વિધાનો સત્ય છે ? પ્રત્યેક `a ∈ N` માટે `(a, a) ∈ R`
View Solution`R` એ `N` થી નો સંબંધ છે. `R = {(a, b) : a, b ∈ N` અને `a = b^(2)`} થાય તે રીતે વ્યાખ્યાયિત છે, તો શું નીચેનાં વિધાનો સત્ય છે ? જો `(a, b) ∈ R`, તો `(b, a) ∈ R`
View Solution`R` એ `N` થી નો સંબંધ છે. `R = {(a, b) : a, b ∈ N` અને `a = b^(2)`} થાય તે રીતે વ્યાખ્યાયિત છે, તો શું નીચેનાં વિધાનો સત્ય છે ? જો `(a, b) ∈ R`, `(b, c) ∈ R` તો `(a, c) ∈ R` પ્રત્યેક વિધાનમાં તમારા જવાબની સત્યાર્થતા ચકાસો.
View Solution`A={1,2,3,4}, B = {1,5,9,11,15,16}` અને `f= {(1,5), (2,9), (3,1), (4,5), (2,11)}`, તો શું નીચેના વિધાનો સત્ય છે? `f` એ `A` થી `B` નો સંબંધ છે.
View Solution`A={1,2,3,4}, B = {1,5,9,11,15,16}` અને `f= {(1,5), (2,9), (3,1), (4,5), (2,11)}`, તો શું નીચેના વિધાનો સત્ય છે? `f` એ `A` થી `B` પરનું વિધેય છે. પ્રત્યેક વિકલ્પમાં તમારા જવાબની સત્યાર્થતા ચકાસો.
View Solution`f` એ `Z xx Z` નો ઉપગણ છે. જો `f= {(ab, a+ b): a, b ∈ Z}` થી વ્યાખ્યાયિત છે, તો શું `f` એ `Z` થી `Z` નું વિધેય છે? તમારા જવાબની સત્યાર્થતા ચકાસો.
View Solution`A = {9,10,11,12,13}` અને `f: A rarr N`, `f (n) = n` નો મહત્તમ અવિભાજ્ય અવયવ છે. `f` નો વિસ્તાર મેળવો.
View Solution
Exercise questions and complete solutions for chapter સંબંધ અને વિધેયો of NCERT Maths(Gujarati) of Class 11