Complete Solutions to EXAMPLES of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| NCERT TAMIL | EXAMPLES |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
Find the angle between force `F= (3hati+4hatj-5hatk)` unit and displacement `d= (5hati+4hatj+3hatk)` unit. Also find the projection of F and d.
View SolutionIt is well known that a rain drop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop, but is otherwise undetermined. Consider a drop of mass 1.0g falling from a height of 1.00km. It hits the ground with a speed of `50.0ms^(-1)` (a) What is the work done by the gravitational force ? (b) What is the work done by the unknown resistive force ?
View SolutionIt is well known that a rain drop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop, but is otherwise undetermined. Consider a drop of mass 1.0g falling from a height of 1.00km. It hits the ground with a speed of `50.0ms^(-1)` (a) What is the work done by the gravitational force ? (b) What is the work done by the unknown resistive force ?
View SolutionA car comes to a sliding stop in 5 m. During this process, the force on the car due to road is 100 N and is directed opposite to the motion.
(a) How much work done the road do on the car?
(b) How much work done the car do on the road?
View SolutionA cyclist comes to a skidding stop in `10m`. During this process, the force on the cycle due to the road is `200N` and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?
View SolutionIn some demonstration, a police officer fires a bullet of mass 50.0g with speed `200ms^(-1)` on soft plywood of thickness 2.00 cm. The bullet emerges with only 10% of its initial kinetic energy. What is the emergent speed of the bullet?
View SolutionA woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100N over a distance of 10m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50N. The total distance through which trunk has been moved is 20m. Plot the force applied by the woman and the frictional force, which is 50N against the distance. Calculat the work done by the two forces over 20m.
View SolutionA block of mass `m=1kg` moving on a horizontal surface with speed `v_(i)=2ms^(-1)` enters a rough patch ranging from `x0.10m to x=2.01m`. The retarding force `F_(r)` on the block in this range ins inversely proportional to x over this range
`F_(r)=-(k)/(x) fo r 0.1 lt xlt 2.01m`
`=0` for `lt 0.1m` and `x gt 2.01m` where `k=0.5J`. What is the final K.E. and speed `v_(f)` of the block as it crosses the patch?
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(0)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) `v_(0)` (ii) the speeds at points B and C, (ii) the ration of kinetic energies `(K_(B)//K_(C))` at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
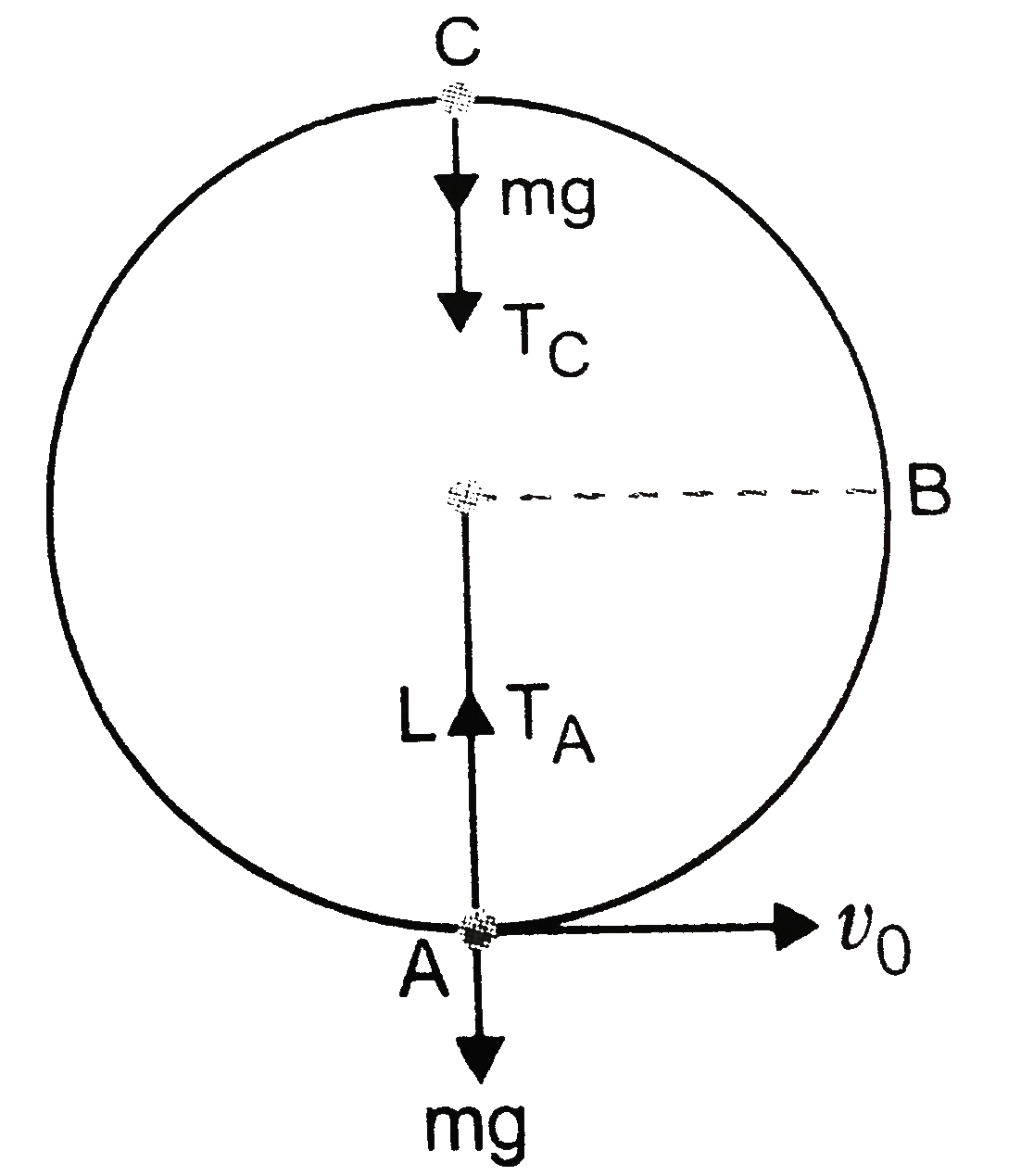
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(0)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) `v_(0)` (ii) the speeds at points B and C, (ii) the ration of kinetic energies `(K_(B)//K_(C))` at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.

View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(0)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) `v_(0)` (ii) the speeds at points B and C, (ii) the ration of kinetic energies `(K_(B)//K_(C))` at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.

View SolutionTo stimulat car accidents, the auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000kg moving with a speed of `18.0 km//h` on a smooth road and colliding with a horizontally mounted spring of spring constant `6.25xx10^(3)Nm^(-1)`. What is the maximum compression of the spring?
View SolutionConsider Example 6.8 taking the coefficient of friction, u, to be `0.5` and calculate the maximum compression of the spring.
View SolutionEnergy required to break one bond in DNA is approximately
View SolutionExpress (a) the energy required to break one bond in DNA `(10^(-10)J)` in eV.
(b) the kinetic energy of an air molecule `(10^(-21)J)` in eV.
(c) the daily intake of a human adult `(10^(7)J)` in kilocalories.
View SolutionExpress (a) the energy required to break one bond in DNA `(10^(-10)J)` in eV.
(b) the kinetic energy of an air molecule `(10^(-21)J)` in eV.
(c) the daily intake of a human adult `(10^(7)J)` in kilocalories.
View SolutionAn elevator can carry a maximum load of `1800 kg` (elevator + passengers) is moving up with a constant speed of `2 ms^(-1)`. The friction force opposite the motion is `4000 N`.What is minimum power delivered by the motor to the elevator?
View SolutionIn a nuclear reactor, a neutron of high speed `(~~10^(7)ms^(-1))` must be slowed down to `10^(3)ms^(-1)` so that it can have a high probality of interacting with isotipe `_92U^(235)` and causing it to fission. Show that a neutron can lose most of its K.E. in an elastic collision with a light nuclei like deuterium or carbon which has a mass of only a fewe times the neutron mass. The material making up the light nuclei usually heavy water `(D_(2)O)` or graphite is called modertaor.
View SolutionConsider the collision depicted in Figure, to be between two billiard balls with equal masses `m_(1)=m_(2)`. The first ball is called the cue and the second ball is called the target. The billiard player wants to sink the target ball in a corner pocket, which is at an angle `theta_(2)=phi=37^(@)`. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain `theta_(1)=theta` .
View Solution
EXAMPLES questions and complete solutions for chapter WORK, ENERGY AND POWER of FULL MARKS PHYSICS(TAMIL) of Class 11