Complete Solutions to EXAMPLE of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| TAMILNADU GOVT | EXAMPLE |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
A box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is `30^(@)`, find the work done by the force.

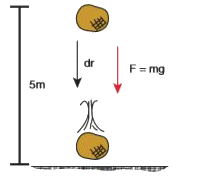
View SolutionAn object of mass 2 kg falls from a height of 5 m to the ground. What is the work done by the gravitational force on the object? (Neglect air resistance, Take g = 10 m `s^(-2)`)
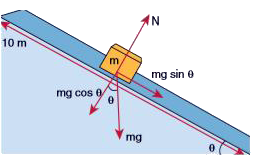
View SolutionAn object of mass m = 1 kg is sliding from top to bottom in the frictionles inclined plane of inclinationangle `theta=30^(@)` and the lengthh of inclined plane is 10 m as shown in the figure. Calculate the work done by gravtiational force and normal force on the object. Assume acceleration due to gravity, g = 10 m `s^(-2)`
View SolutionIf an object of mass 2 kg is thrown up from the ground reaches a height of 5 m and falls back to the Earth (neglect the air resistance). Calculate
The work done by gravity when the object reaches 5 m height
View SolutionIf an object of mass 2 kg is thrown up from the ground reaches a height of 5 m and falls back to the Earth (neglect the air resistance). Calculate
The work done by gravity when the object comes back to Earth
View SolutionIf an object of mass 2 kg is thrown up from the ground reaches a height of 5 m and falls back to the Earth (neglect the air resistance). Calculate
Total work done by gravity both in upward and downward motion and mention the physical significance of the result.
View SolutionA weight lifter lifts a mass of 250 kg with a force 5000 N to the height of 5 m.
What is the workdone by the weight lifter?
View SolutionA weight lifter lifts a mass of 250 kg with a force 5000 N to the height of 5 m.
What is the workdone by the gravity?
View SolutionA weight lifter lifts a mass of 250 kg with a force 5000 N to the height of 5 m.
What is the net workdone on the object?
View SolutionA variable force `F=kx^(2)` acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle form x = 0 m to x = 4 m.
(Assume the constant k = 1 N `m^(-2)`)
View SolutionTwo objects of masses 2 kg and 4 kg are moving with the same momentum of 20 kg `ms^(-1)`.
Will they have same kinetic energy?
View SolutionTwo objects of masses 2 kg and 4 kg are moving with the same momentum of 20 kg `ms^(-1)`.
Will they haved same speed?
View SolutionAn object of mass 2 kg is taken to a height 5 m from the ground (g = 10 m `s^(-2)`).
Calculate the potential energy stored in the object.
View SolutionAn object of mass 2 kg is taken to a height 5 m from the ground (g = 10 m `s^(-2)`).
Where does this potential energy come from?
View SolutionAn object of mass 2 kg is taken to a height 5 m from the ground (g = 10 m `s^(-2)`).
What external force must act to bring the mass to that height?
View SolutionAn object of mass 2 kg is taken to a height 5 m from the ground (g = 10 m `s^(-2)`).
What is the net force that acts on the object while the object is taken to the height 'h'?
View SolutionLet the two springs A and B be such that `k_(A) gt k_(B)`. On which spring will more work has to be done if they are stretched by the same force?
View SolutionA body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.
Calculate the potential energy stored in the spring-mass system?
View SolutionA body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.
What is the work done by the spring force in this elongation?
View SolutionA body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.
Suppose the spring is compressed to the same 25 cm, calculate the potential energy stored and also the work done by the spring force during compression. (The spring constant, k = 0.1 N `m^(-1)`).
View SolutionCompute the work done by the gravitational force for the following cases.
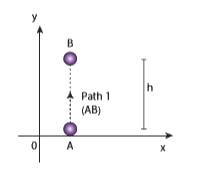
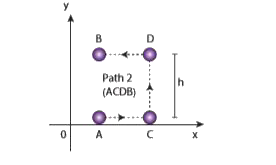
View SolutionConsider an object of mass 2 kg moved by an external force 20 N in a surface having coefficient of kinetic friction 0.9 to a distance 10 m. What is the work done by the external force and kinetic friction ? Comment on the result. (Assume g = 10 `ms^(-2)`)
View SolutionAn object of mass 1 kg is falling from the height h = 10 m. Calculate
The total energy of an object at h = 10 m
(Assume g = 10 `ms^(-2)`)
View SolutionAn object of mass 1 kg is falling from the height h = 10 m. Calculate
Potential energy of the object when it is at h = 4 m
(Assume g = 10 `ms^(-2)`)
View SolutionAn object of mass 1 kg is falling from the height h = 10 m. Calculate
Kinetic energy of the object when it is at h = 4 m
(Assume g = 10 `ms^(-2)`)
View SolutionAn object of mass 1 kg is falling from the height h = 10 m. Calculate
What will be the speed of the object when it hits the ground?
(Assume g = 10 `ms^(-2)`)
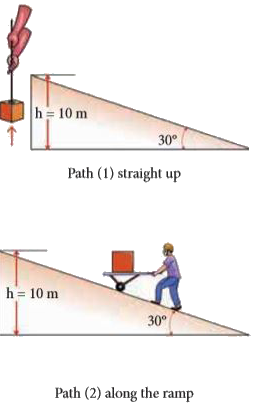
View SolutionA body of mass 100 kg is lifted to a height 10 m from the ground in two different ways as shown in the figure. What is the work done by the gravity in both the cases? Why is it easier to take the object through a ramp?
View SolutionAn object of mass m is projected from the ground with initial speed `v_(0)`
`" "`Find the speed at height h.
View SolutionAn object of mass 2 kg attached to a spring is moved to a distance x = 10 m from its equilibrium position. The spring constant k = 1 N `m^(-1)` and assume that the surface is frictionless.
When the mass crosses the equilibrium position, what is the speed of the mass?
View SolutionAn object of mass 2 kg attached to a spring is moved to a distance x = 10 m from its equilibrium position. The spring constant k = 1 N `m^(-1)` and assume that the surface is frictionless.
What is the force that acts on the object when the mass crosses the equilibrium position and extremum position `x=pm10m`.
View SolutionWater in a bucket tied with rope is whirled around in a vertical circle of radius 0.5 m. Calculate the minimum velocity at the lowest point so that the water does not spill from it in the course of motion.
`(g=10ms^(-2))`
View SolutionCalculate the energy consumed in electrical units when a 75 W fan is used for 8 hours daily for one month (30 days).
View SolutionA vehicle of mass 1250 kg is driven with an acceleration 0.2 `ms^(-2)` along a straight level road against an external resistive force 500 N. Calculate the power delivered by the vehicle's engine if the velocity of the vehicle is 30 `ms^(-1)`.
View SolutionA lighter particle moving with a speed of 10 m `s^(-1)` collides with an object of double its mass moving in the same direction with half its speed. Assume that the collision is a one dimensional elastic collision. What will be the speed of both particles after the collision?
View SolutionA bullet of mass 50 g is fired from below into a suspended object of mass 450 g. The object rises through a height of 1.8 m with bullet remaining inside the object. Find the speed of the bullet. Take `g=10ms^(-2)`.
View SolutionShow that the ratio of velocities of equal masses in an inelastic collision when one of the masses is stationary is `v_(1)/v_(2)=(1-e)/(1+e)`.
View Solution
EXAMPLE questions and complete solutions for chapter WORK, ENERGY AND POWER of FULL MARKS PHYSICS(TAMIL) of Class 11