Complete Solutions to EXAMPLES of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NCERT TAMIL | EXAMPLES |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
On an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
View SolutionWhich of the following functions of time represent periodic and non-periodic motion?
(a) `sin omegat+cos omegat` (b) `e- omegat`
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic? Give the period for each case.
(1) `sinomegat-cosomegat`
(2) `sin^(2)omegat`
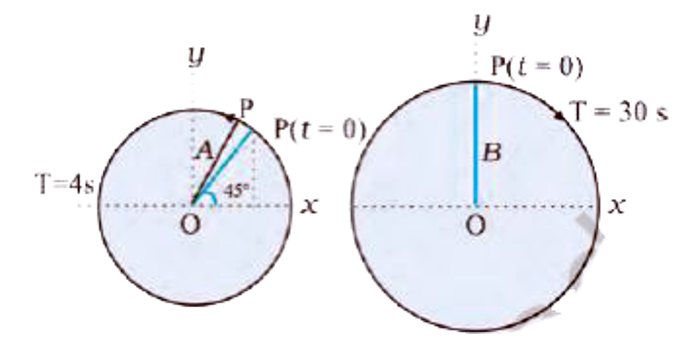
View SolutionThe figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated in the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionA body oscillates with SHM according to the equation (in SI units),
`x = 5 cos [2pi t + pi//4]`.
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.
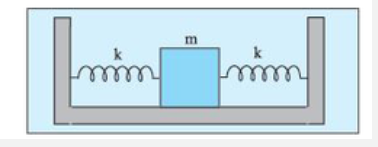
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of `50 N m^(-1)`. The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N `m^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
View SolutionWhat is the length of a simple pendulum, which ticks seconds ?
View SolutionFor the damped oscillator shown in Fig. 14.19, the mass m of the block is 200 g, k = 90 N `m^(-1)` and the damping constant b is 40 g `s^(-1)`. Calculate (a) the period of oscillation, (b) time taken for its amplitude of vibrations to drop to half of its initial value, and (c) the time taken for its mechanical energy to drop to half its initial value.
View Solution
EXAMPLES questions and complete solutions for chapter OSCILLATIONS of FULL MARKS PHYSICS(TAMIL) of Class 11