Complete Solutions to examples of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| NN GHOSH | examples |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
A particle executes simple harmonic motion of period `16 s`. Two seconds later after it passes through the center of oscillation its velocity is found to be `2 m//s`. Find the amplitude.
View SolutionA body executing SHM has an amplititude of 10 cm and its time period is 1.5s. Calcualte the time taken by the body to travel a distance of `5sqrt(3)` cm from its rest position.
View SolutionWrite the equation for a particle in simple harmonic motion with amplitude a and angular frequency `epsilon` considering all distance from one extreme position and time when its is at the other extreme position.
View SolutionFind the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
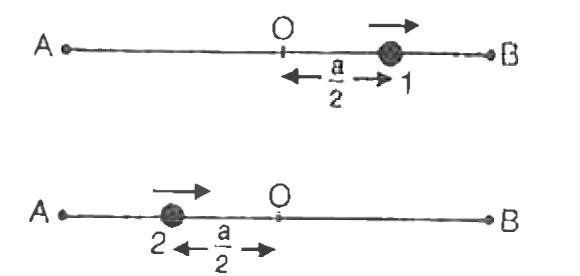
View SolutionA spring of force constant k and negligible mass is attached to a rigid mass m at one end and clamped to a strong support at the other. The mass is displaced a little and then released. Show that the body executes simple harmonic motion and calculate its time period. If the spring is cut into three equal pieces and the same body is supported by one such piece in a smaller way, by how much will the time period be increased or decreased?
View SolutionA uniform U-tube contains a very slightly mobile liquid to a height of 50 cm in each limb. If the liquid in one lime is depressed and then released, find the period of oscialltion of the liquid in the tube.
View SolutionTwo cubes of mass `m_(1)` and `m_(2)` are interconnected by a weightless spring of stiffness k and placed on a smooth horizontal table. Then the cubes are drawn closer to each other and released. Find the frequency of oscillation.

View SolutionA smooth horizontal disc rotates about the vertical axis `O` (figure) with a constant angular velocity `omega`. A thin uniform rod `AB` of length `l` performs small oscillation about the vertical axis `A` fixed to the disc at a distance `a` from the axis of the disc. Find the frequency `omega_(0)` of these oscillations.

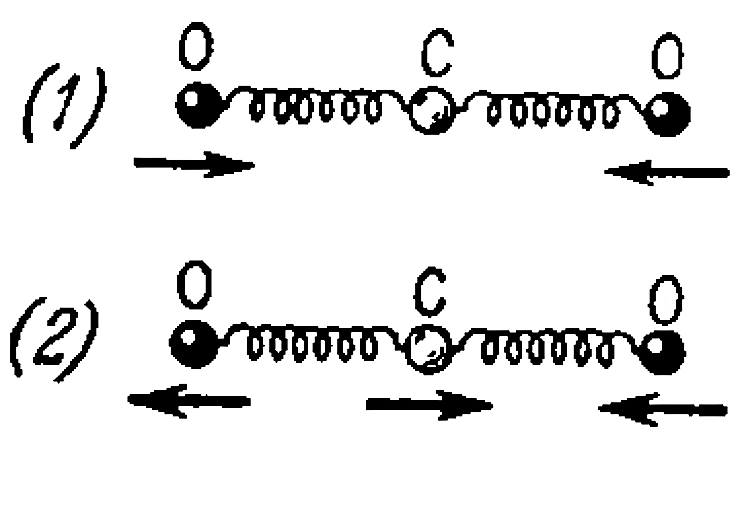
View SolutionA mock`-` up of a `CO_(2)` molecule consists of three balls interconnected by identical light springs and placed along a straight line in the state of equilibrium. Such a system can freely perform oscillation of two types, as shown by the arrows in figure. Knowing the masses of the atomes, find the ration of frequencies of these oscillations
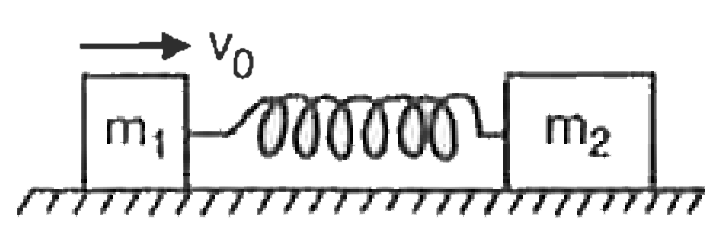
View SolutionTwo bodies with masses `m_(1)` = 1kg and `m_(2)`= 2kg are connected by a spring of force constant `k=24Nm^(-1)`. The left ball is imparted an initial velocity `v_(0)`=12 cm/s. Find (a) the frequency of the oscillations (b) the energy and the amplitude of the osciallations.
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form u(x) = `a/x^(2)-b/x)`, where a and b are positive constants. Find the period of small oscillations of the particle.
View SolutionFind the period of small osciallations in a vertical plane performed by a small ball of mass m=50g fixed at the middle of a thin horizontal string of length l=1m and tensioned with a constant force T = 100N
View Solution
examples questions and complete solutions for chapter SIMPLE HARMONIC MOTION of BHARATI BHAWAN PHYSICS (HINGLISH) of Class 11