Complete Solutions to प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.2) of chapter सम्बन्ध एवं फलन of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | सम्बन्ध एवं फलन |
| MADHUR GUPTA | प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.2) |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
माना लीजिए कि A = {1, 2, 3, …,14} R ={x, y : 3x - y = 0, जहाँ `x, y in A`} द्वारा A से A का एक सम्बन्ध R लिखिए । इसके प्रान्त, सह-प्रान्त और परिसर लिखिए ।
View Solutionप्राकृत संख्याओं के समुच्चय पर R = (x, y): y = x+ 5, x संख्या 4 से कम, एक प्राकृत संख्या है, `x, y in N`} द्वारा एक सम्बन्ध R परिभाषित कीजिए । इस सम्बन्धों को रोस्टर रूप में तथा इसके प्रान्त और परिसर लिखिए ।
View SolutionA = {1, 2, 3, 5} और B = {4, 6, 9}| A से B में एक सम्बन्ध R = {(x, y): x और y का अन्तर विषम है, `x in A, y in B}` द्वारा परिभाषित कीजिए । R को रोस्टर रूप में लिखिए ।
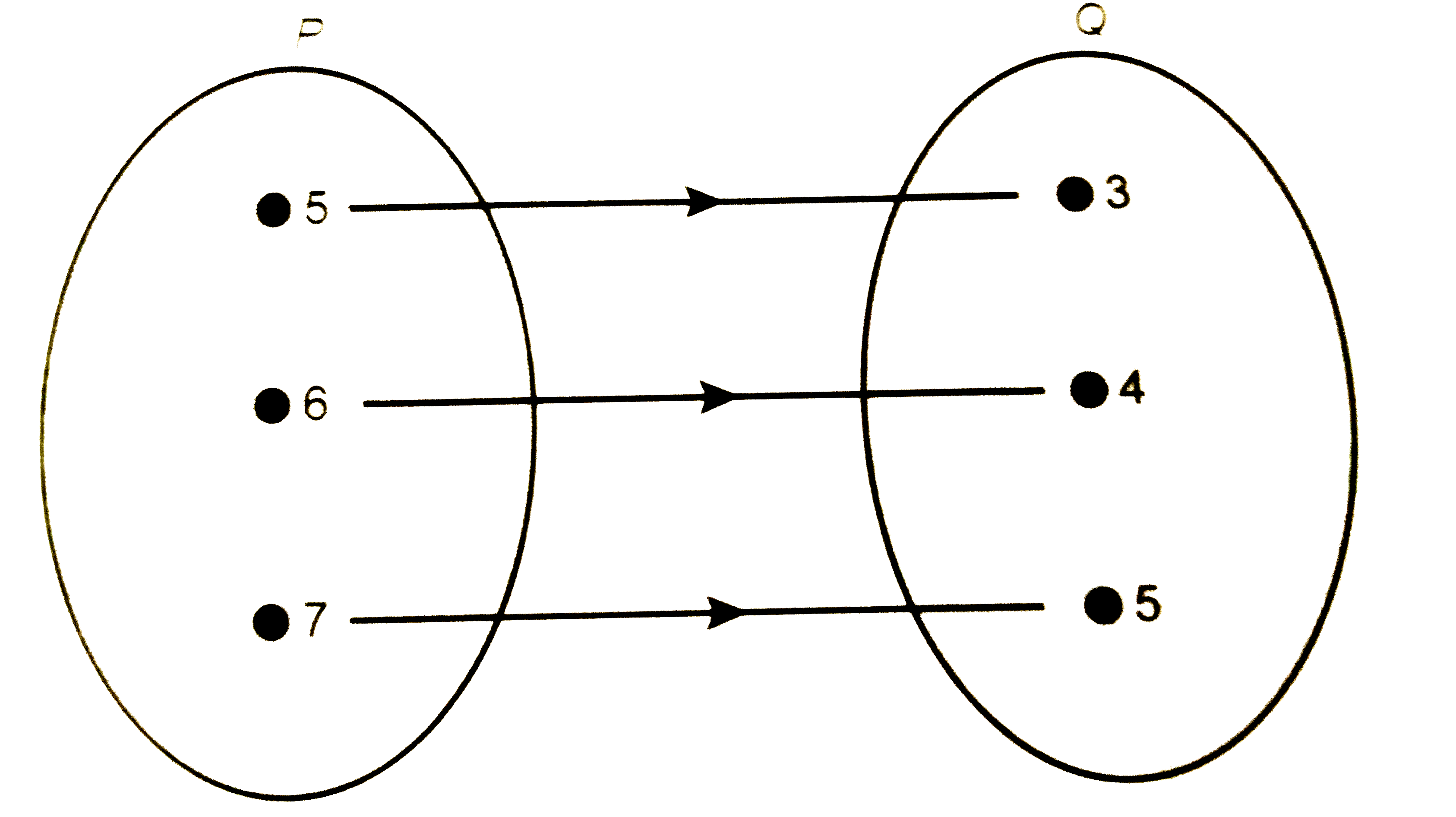
View Solutionआकृति समुच्चय P से Q का एक सम्बन्ध दर्शाती इस सम्बन्ध को
(i) समुच्चय निर्माण रूप
(ii) रोस्टर रूप में लिखिए । इसके प्रान्त तथा परिसर क्या हैं?
View Solutionमान लीजिए कि A = {1, 2, 3, 4, 6} । मान लीजिए कि R, A पर `{(a, b) : a, b in A` संख्या a संख्या b को यथावत विभाजित करती है} द्वारा परिभाषित एक सम्बन्ध है ।
(i) R को रोस्टर प्रान्त में लिखिए
(ii) R का प्रान्त ज्ञात कीजिए
(iii) R का परिसर ज्ञात कीजिए ।
View Solution`R = {(x, x +5) : x in {0, 1, 2, 3, 4, 5} ` द्वारा परिभाषित सम्बन्ध R के प्रान्त और परिसर ज्ञात कीजिए ।
View Solutionसम्बन्ध `R = {(x, x^(3)) :x` संख्या 10 से कम एक अभाज्य संख्या है} को रोस्टर रूप में लिखिए ।
View Solutionमान लीजिए कि A = {x,y, z} और B = {1, 2}, A से B के सम्बन्धों कि संख्या ज्ञात कीजिए ।
View Solutionमान लीजिए कि R, Z पर R = {(a, b) : a, b `in ` Z, a-b एक पूर्णांक है} द्वारा परिभाषित एक सम्बन्ध है । R के प्रान्त तथा परिसर ज्ञात कीजिए ।
View Solution
प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.2) questions and complete solutions for chapter सम्बन्ध एवं फलन of NAGEEN MATHS (HINDI) of Class 11
All Exercises from MADHUR GUPTA Class 11 MATHS सम्बन्ध एवं फलन
- प्रश्नावली ( विविध प्रश्नावली )
- प्रश्नावली 2A
- प्रश्नावली 2B
- प्रश्नावली 2C
- प्रश्नावली 2D (निम्नलिखित फलनों के प्रान्त ज्ञात कीजिए -)
- प्रश्नावली 2D(निम्नलिखित फलनों के प्रान्त और परिसर ज्ञात कीजिए -)
- प्रश्नावली 2E
- प्रश्नावली 2F (बहुविकल्पीय प्रश्न )
- प्रश्नावली 2G (प्रतियोगी परीक्षाओं हेतु प्रश्न )
- प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.1)
- प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.2)
- प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.3)
- साधित उदाहरण