Complete Solutions to साधित उदाहरण of chapter सम्बन्ध एवं फलन of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | सम्बन्ध एवं फलन |
| MADHUR GUPTA | साधित उदाहरण |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
यदि A = {1, 2, 3} और B = {x, y}, तो `A xx B` को तीर आरेख द्वारा निरूपित कीजिए ।
View Solutionयदि (2x + 3, y - 1) = (3, 5), तो x और y के मान ज्ञात कीजिए ।
View Solutionयदि A = {3, 4} तथा B = {2, 3, 4}, तो `A xx B` का मान ज्ञात कीजिए ।
View Solutionयदि A = {1, 2} तथा B = {2, 3}, तो दिखाइए कि-
`A xx B ne B xx A`
View Solutionयदि `A xx B = {a, x), (a, y), (b, x), (b, y)}, तो A और B ज्ञात कीजिए ।
View Solutionयदि A और B दो समुच्च हैं तथा n`(A xx B) = 6` हैं । यदि `A xx B` के तीन अवयव (1, 2), (2, 3), (3, 3) हैं, तो `A xx B` और `B xx A` ज्ञात कीजिए ।
View Solutionयदि A = {a, b}, B = {2, 3} और C = {3, 4}, तो -
(i) `A xx (B nn C)`
(ii) `A xx (B uu C)` ज्ञात कीजिए ।
View Solutionयदि `A sube B` और C कोई समुच्च है, तो सिद्ध कीजिए कि-
`A xx C sube B xx C`
View Solutionयदि `A sube B` और `C sube D`, तो सिद्ध कीजिए कि-
`A xx C sube B xx D`
View Solutionकिन्ही चार समुच्चयों A, B, C और D के लिये सिद्ध कीजिए कि-
`(A xx B) nn (C xx D) = (A nn C) xx (B nn D)`
View Solutionयदि समुच्चयों A और B में `n` अवयव सर्वनिष्ठ है, तो सिद्ध कीजिए `A xx B` और `B xx A` में `n^(2)` अवयव सर्वनिष्ठ होंगे ।
View Solutionप्राकृतिक संख्याओं के समुच्च N से N में निम्नलिखित सम्बन्ध व्यक्त किये गये हैं-
`(a) R_(1)` = {(1, 1), (4, 2), (9, 3), (16, 4), … }
(b) `R_(2)` = {(3, 1), (4, 2), (5, 3), (6, 4),…}
उक्त प्रत्येक सम्बन्ध को निर्माण रूप में व्यक्त कीजिए ।
View Solutionनिम्नांकित आकृति में समुच्चय P से Q में एक सम्बन्ध R दर्शाया गया है-
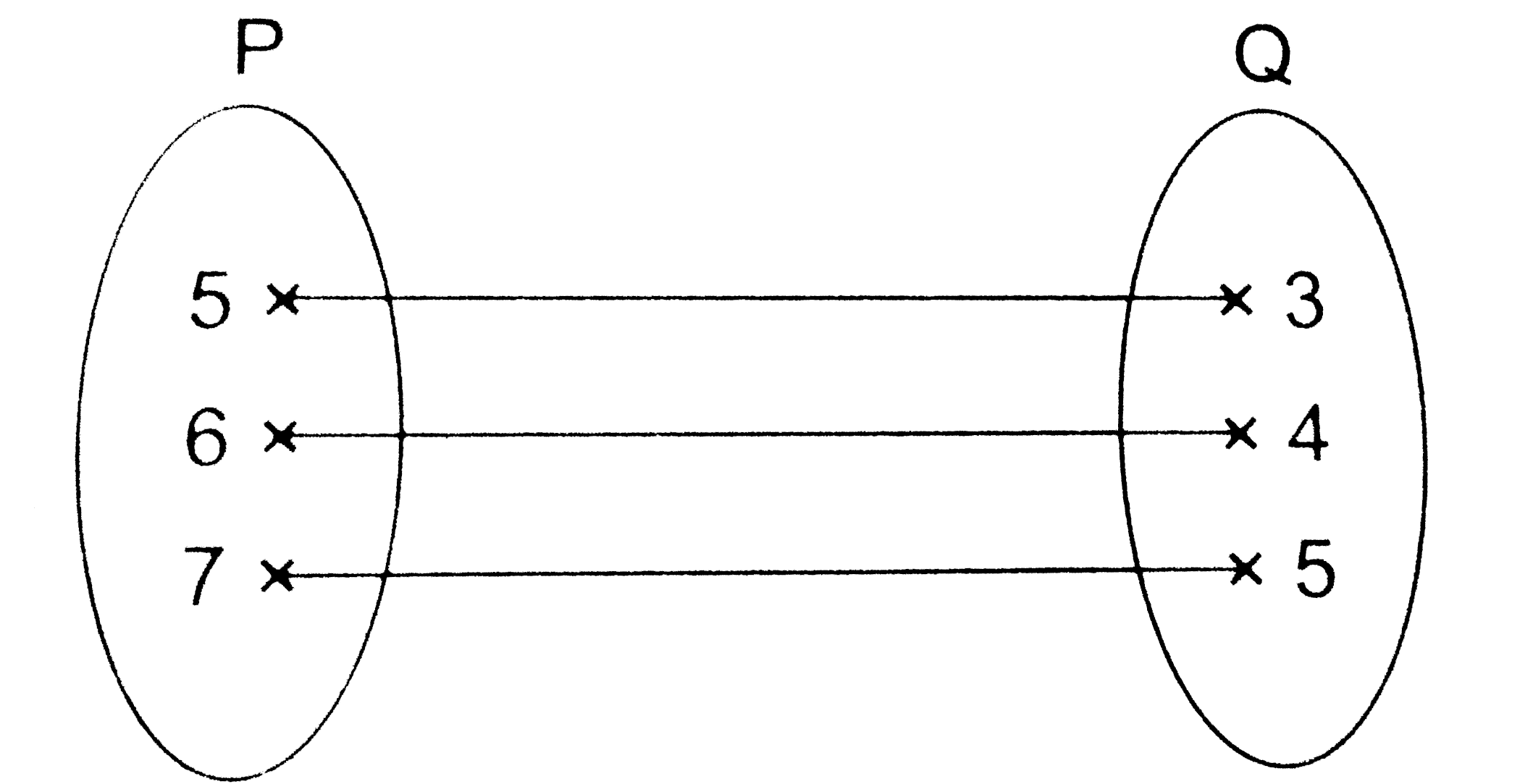
उक्त सम्बन्ध को रोस्टर रूप तथा समुच्चय निर्माण रूप में लिखिए। सम्बन्ध के प्रान्त और परिसर ज्ञात कीजिए ।
View Solutionयदि A = {1,2, 3} और B = {4, 5, 6}, तो निम्नलिखित में कौन समुच्चय A से B में एक सम्बन्ध है? कारण सहित बताइए-
(a) `R_(1)` = {(1, 5), (2, 4), (3, 5)}
(b) `R_(2)` = {(4, 1), (2, 6), (5, 1), (2, 4)}
(c) `R_(3)` = {(1, 4), (2, 5), (3, 4), (2, 6), (3, 6)}
(d) `A xx B`
View Solutionमाना R समुच्चय Q से Q में एक सम्बन्ध निम्न प्रकार परिभाषित है-
R = {(a, b) : a, b, `in ` Q, और a-b `in` Z}
सिद्ध कीजिए कि-
(i) प्रत्येक `a in Q` के लिये (a, a) `in ` R
(ii) (a, b) `in R rArr (b, a) in R` जबकि `a, b in Q`
(iii) `(a, b) in R, (b, c) in R rArr (a, c) in R` जबकि `a, b, c in Q`
View Solutionनिम्नलिखित संबंधों में से प्रत्येक का निरीक्षण करके कारण सहित बताइए कि वह एक फलन है अथवा नहीं-
(i) `R_(1)` = {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
`(ii) `R_(2)` = {(2,1), (4, 2), (6, 3), (8, 4) (10, 5), (12, 6), (14, 7)}
(iii) `R_(3)` = {(1, 3), (1, 5), (2, 5)}
View Solutionयदि A = {1, 2, 3} और B = {2, 3, 4}, तो ज्ञात कीजिए कि निम्नलिखित में से कौन-कौन A से B में फलन हैं?
(i) f = {(1, 2), (2, 3), (3, 4)}
(ii) g = {(1, 2), (1, 3), (2, 3), (3, 4)}
(iii) h = {(1, 3), (2, 4)}
View Solutionमाना R, प्राकृतिक संख्याओं के समुच्चय N पर परिभाषित एक सम्बन्ध एक प्रकार है कि-
`R = {(x, y) : y = 2x, x, y in N`}
क्या R, N से N में एक फलन है? यदि हाँ तो R का प्रान्त, सह-प्रान्त और परिसर ज्ञात कीजिए ।
View Solutionयदि f= {(1, 1), (2, 3), (3, 5), (4, 7)}, Z से Z में एक रैखिक फलन है, तो f(x) ज्ञात कीजिए ।
View Solutionमाना A दो धन पूर्णांकों का समुच्चय है तथा फलन `f:A to Z^(+)` निम्नवत परिभाषित है -
`f(n) =p` जहाँ `p, n` का महत्तम अभाज्य गुणनखण्ड है ।
यदि `f` का परिसर `{3}` है, तो `A` ज्ञात कीजिए । क्या `A` अद्वितीय रूप से निर्धारित किया जा सकता है?
View Solutionयदि f(x) = x^(2)+ 5x-3, तो f(4) का मान ज्ञात कीजिए ।
View Solutionयदि `f(x) = 2 (1 + "sin"x)`, तो `f((pi)/(2))` का मान ज्ञात कीजिए ।
View Solutionयदि `f : R to R` निम्न प्रकार परिभाषित हैं
`f(x) = {(2x + 5","x gt 9), (x^(2)-1","-9 lt x lt 9), (x-4"," x lt -9):}`
तो (i) f (2), (ii) f(10), (iii) f(-12) और (iv) f[f(3)] के मान ज्ञात कीजिए ।
View Solutionयदि `f(x) = x^(3) - (1)/(x^(3))`, तो `f(x) + f(-x)` का मान ज्ञात कीजिए ।
View Solutionमाना f एक वास्तविक फलन है, जो `f(x) = (x -1)/(x + 1)` से परिभाषित है । सिद्ध कीजिए की `f(2x) = (3f(x)+1)/(f(x) + 3)`
View Solutionयदि `y = f(x) = (x+2)/(x-1), x ne 1`, तो दर्शाइए कि x = f(y).
View Solutionयदि `x ne 0` के लिए
`af (x) + bf (1/x) = (1)/(x) - 5,`
` a ne b`, तो f(x) ज्ञात कीजिए ।
View Solutionयदि f(x) = cotx, तो सिद्ध कीजिए कि f(-x) = -f(x)
View Solutionयदि f(x) = log`(1-x)/(1+x)`, तो दर्शाइए कि `f(a) + f(b) = f((a+b)/(1+ab))`
View Solutionयदि `f(x) = (x-1)/(x+1)`, तो सिद्ध कीजिए कि f{f(x)} = `-(1)/(x)`
View Solutionयदि `f(x) = x^(2)` और g(x) = 2x + 1 दो वास्तविक फलन हैं, तो निम्नलिखित को ज्ञात कीजिए-
`(f+g)(x), (f-g)(x), (f g)(x), ((f)/(g))(x)`
View Solutionफलन `f(x) = (x-3)/(4-x)` का प्रान्त और परिसर ज्ञात कीजिए ।
View Solutionफलन `f(x) = (1)/(sqrt(x-2))` का प्रान्त और परिसर ज्ञात कीजिए ।
View Solutionफलन `f(x) = (x)/(1+x^(2))` का प्रान्त और परिसर ज्ञात कीजिए ।
View Solutionफलन `f(x) = (x^(2)-9)/(x-3)` का प्रान्त और परिसर ज्ञात कीजिए ।
View Solutionफलन `f(x) = (1)/(2-"sin"3x)` का प्रान्त और परिसर ज्ञात कीजिए ।
View Solution
साधित उदाहरण questions and complete solutions for chapter सम्बन्ध एवं फलन of NAGEEN MATHS (HINDI) of Class 11
All Exercises from MADHUR GUPTA Class 11 MATHS सम्बन्ध एवं फलन
- प्रश्नावली ( विविध प्रश्नावली )
- प्रश्नावली 2A
- प्रश्नावली 2B
- प्रश्नावली 2C
- प्रश्नावली 2D (निम्नलिखित फलनों के प्रान्त ज्ञात कीजिए -)
- प्रश्नावली 2D(निम्नलिखित फलनों के प्रान्त और परिसर ज्ञात कीजिए -)
- प्रश्नावली 2E
- प्रश्नावली 2F (बहुविकल्पीय प्रश्न )
- प्रश्नावली 2G (प्रतियोगी परीक्षाओं हेतु प्रश्न )
- प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.1)
- प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.2)
- प्रश्नावली एन सी ई आर टी प्रश्न (प्रश्नवाली 2.3)
- साधित उदाहरण