Complete Solutions to Numberical MCQ single of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| PHYSICS GALAXY | Numberical MCQ single |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA cubical block of copper of side `10cm` is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(`rho_(Hg) = 13.6 g//c c , rho_(Cu) = 7.3 g//c c , rho_(water) = 1gm//c c)`
View SolutionA block of silver of mass `4 kg` hanging from a string is immersed in a liquid of relative density `0.72`. If relative density of silver is `10`, then tension in the string will be
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density `rho` and its end `B` is closed. Then the force exerted by the fluid on the tube at end `B` will be : [Neglect atmospheric pressure and assume the radius of the tube to be negligible in comparison to `l`]

View SolutionFigure shows water filled in a symmetrical container. Four pistons of equal area `A` are used at the four openings to keep the water in equilibrium. Now an additional force `F` is applied at each piston. The increase in the pressure at the centre of the container due to this addition is

View SolutionA block of iron is kept at the bottom of a bucket full of water at `2^@C`. The water exerts bouyant force on the block. If the temperature of water is increased by `1^@C` the temperature of iron block also increases by `1^@C`. The bouyant force on the block by water
View SolutionA `U`-tube of base length `l` filled with the same volume of two liquids of densities `rho` and `2rho` is moving with an acceleration `'a'` on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero, then the height `h` is given by

View SolutionThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities `2rho` and `rho` as shown in the figure is

View SolutionA non uniform cylinder of mass `m`, length `l` and radius `r` having its C.O.M at a distance `(l)/(4)` from centre and lying on axis of cylinder . The cylinder is kept in a liquid of uniform density `rho`. The moment of inertia of the rod about C.O.M is I. The angular acceleration of point A relative to point B just after the rod is released from position shown in figure is .

View SolutionAn incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

View SolutionAn unsymmetrical sprinkler the top view of the setup has frictionless shaft and equal fluid flows through each nozzle with a velocity of 10 m/sec relative to nozzle. If the shaft is rotating at constant angular speed then its angular speed of rotation is :
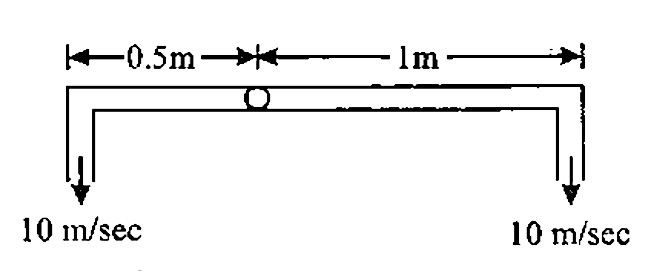
View SolutionThe centre of buoyancy of a floating object is :
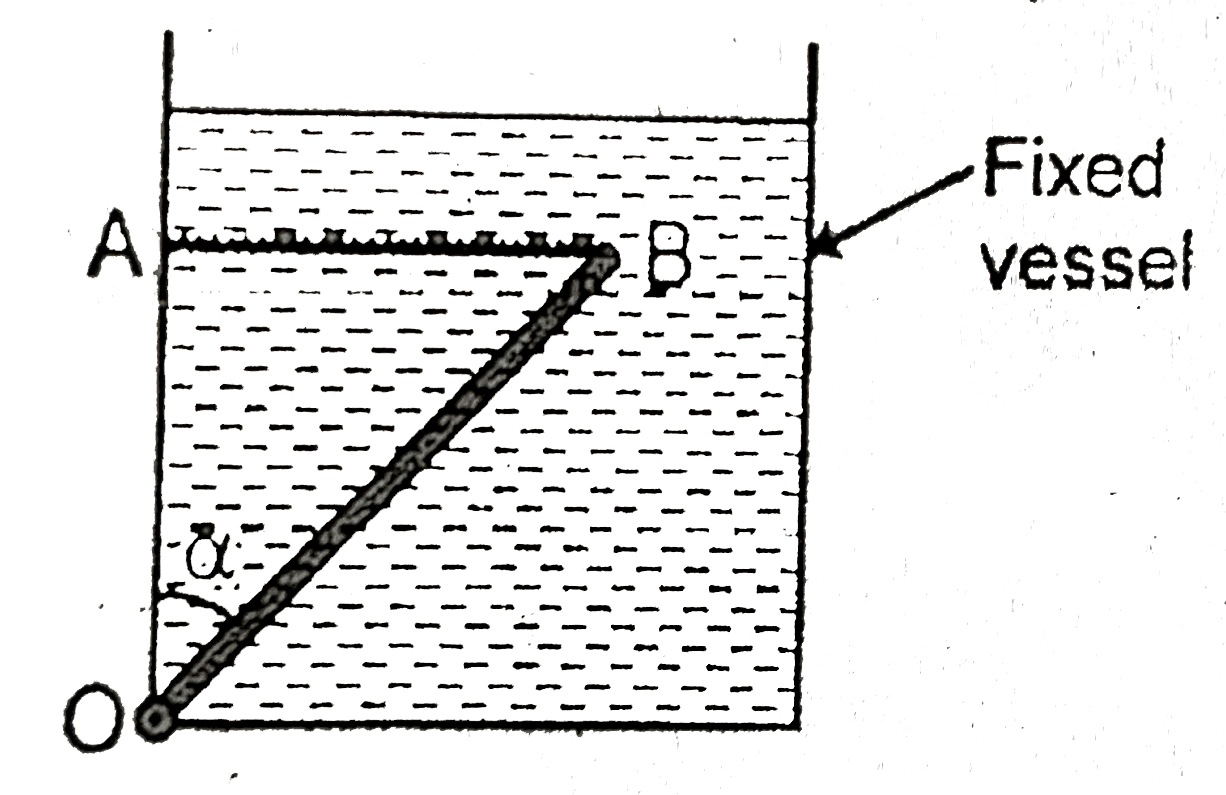
View SolutionA uniform rod `OB` of length `1m`, cross-sectional areal `0.012 m^(2)` and relative density `2.0` is free to rotate about smooth hinge `O` in vertical plane. The rod is held with a horizontal string `AB` which can withstand a maximum tension of `45N`. The rod and string system is kept in water as shown in figure. The maximum value of angle `alpha` which the rod can make with vertical without breaking the string is
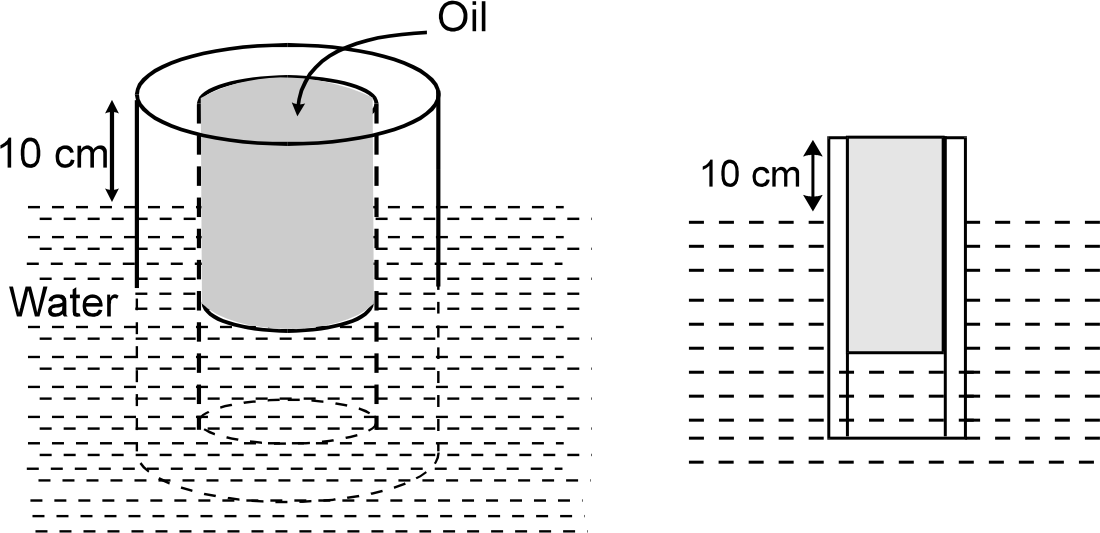
View SolutionA tube with both ends open floats vertically in water. Oil with a density 800 kg/`m^3` is poured into the tube. The tube is filled with oil upto the top end while in equilibrium. The portion out of the water is of length 10 cm. The length of oil in the tube is `10 alpha cm`. Find `alpha` (assume effect of surface tension is neglible):
View SolutionFollowing are some statements about buoyant force : (Liquid is of uniform density)
(i)Buoyant force depends upon orientation of the concerned body inside the liquid.
(ii)Buoyant force depends upon the density of the body immersed.
(iii)Buoyant force depends on the fact whether the system is on moon or on the earth.
(iv)Buoyant force depends upon the depth at which the body (fully immersed in the liquid) is placed inside the liquid. Of these statements :
View SolutionAn ideal fluid is flowing through the given tubes which is placed on a horizontal surface. If the liquid has velocities `V_(A)` and `V_(B)` and pressure `P_(A)` and `P_(B)` at point `A` and `B` respectively, then the correct relation is (`A` and `B` are at same height from ground level. the figure shown is as in the system is seen from the top):
View SolutionThere is a small hole in the bottom of a fixed container containing a liquid upto height `'h'`. The top of the liquid as well as the hole at the bottom are exposed to atmosphere. As the liquid come out of the hole. (Area of the hole is `'a'` and that of the top surface is `'A'`) :
View SolutionA fixed container of height `H` with large cross-sectional area `A` is completely filled with water. Two small orifice of cross-sectional area `a` are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View Solution_S01_019_Q01.png)
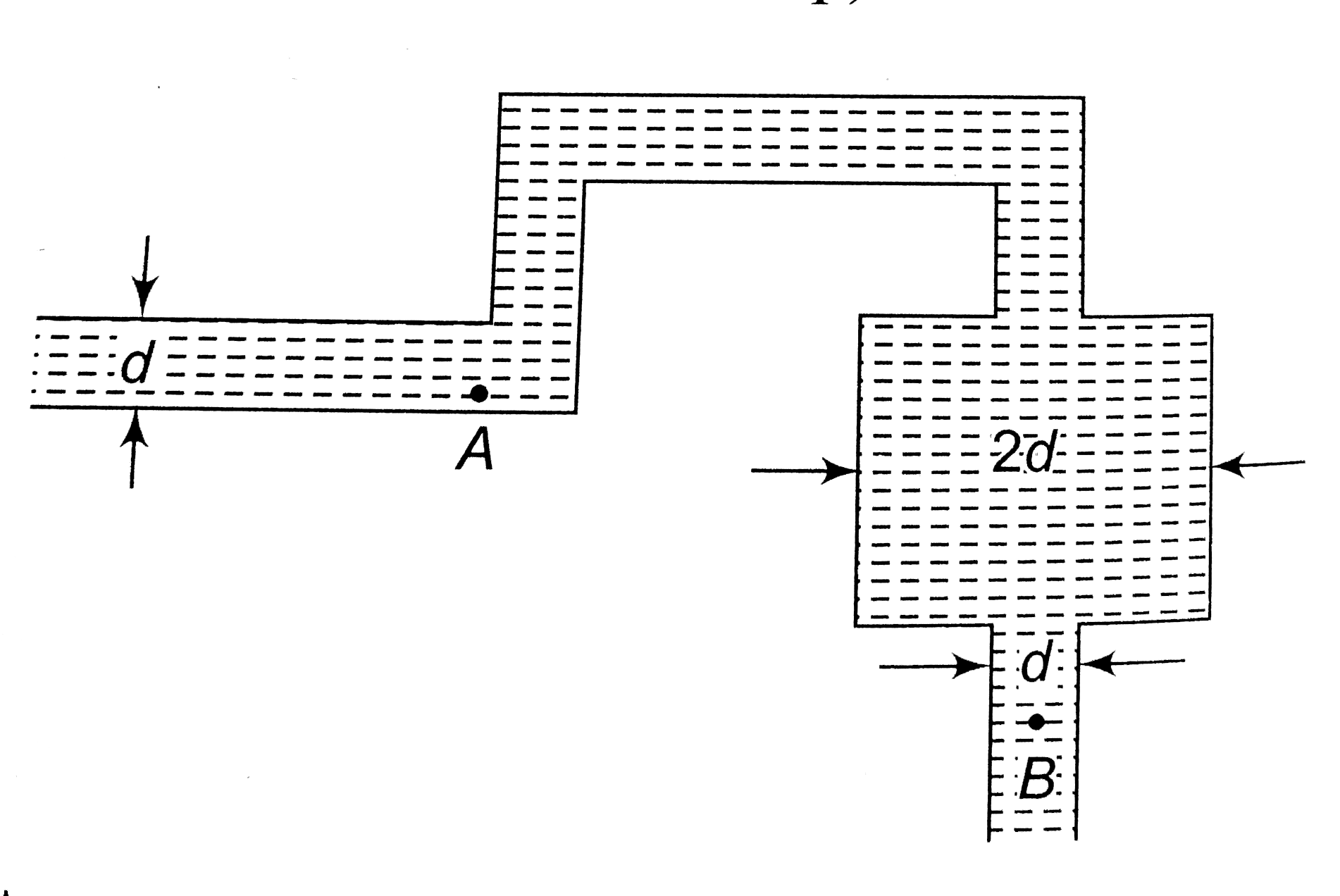
The manometer shown below is used to measure the difference in water level between the two tanks. Calculate this difference for the conditions indicated.
View SolutionA cylinderical vessel filled with water is released on a fixed inclined surface of angle `theta` as shown in figure. The friction coefficient of surface with vessel in `mu(lt tan theta)`. Then the constant with the incline will be (Neglect the viscosity of liquid)

View SolutionA copper piece of mass 10 g is suspended by a vertical spring. The sprig elongates 1 cm over its natural length to keep the piece in equilibrium. A beaker containing water is now placed below the piece so as to immerse the piece completely in water. Find the elongation of the spring. Density of copper =9000 kgm^-3. `Take g=10ms^-2`
View SolutionA vessel contains oil (density `=0.8gm//cm^3`) over mercury (density `=13.6gm cm^3`). A homogeneous sphere floats with half its volume immersed in mercury and the other half in oil. The density of the material of the sphere in `gm//cm^3` is
View SolutionA block is partially immeresed in a liquid and the vessel is accelerating upwards with an acceleration 'a'. The block is observed by two observers `O_1` and `O_2`, one at rest and the other accelerating with an acceleration 'a' upward. The total buoyant force on the block is :
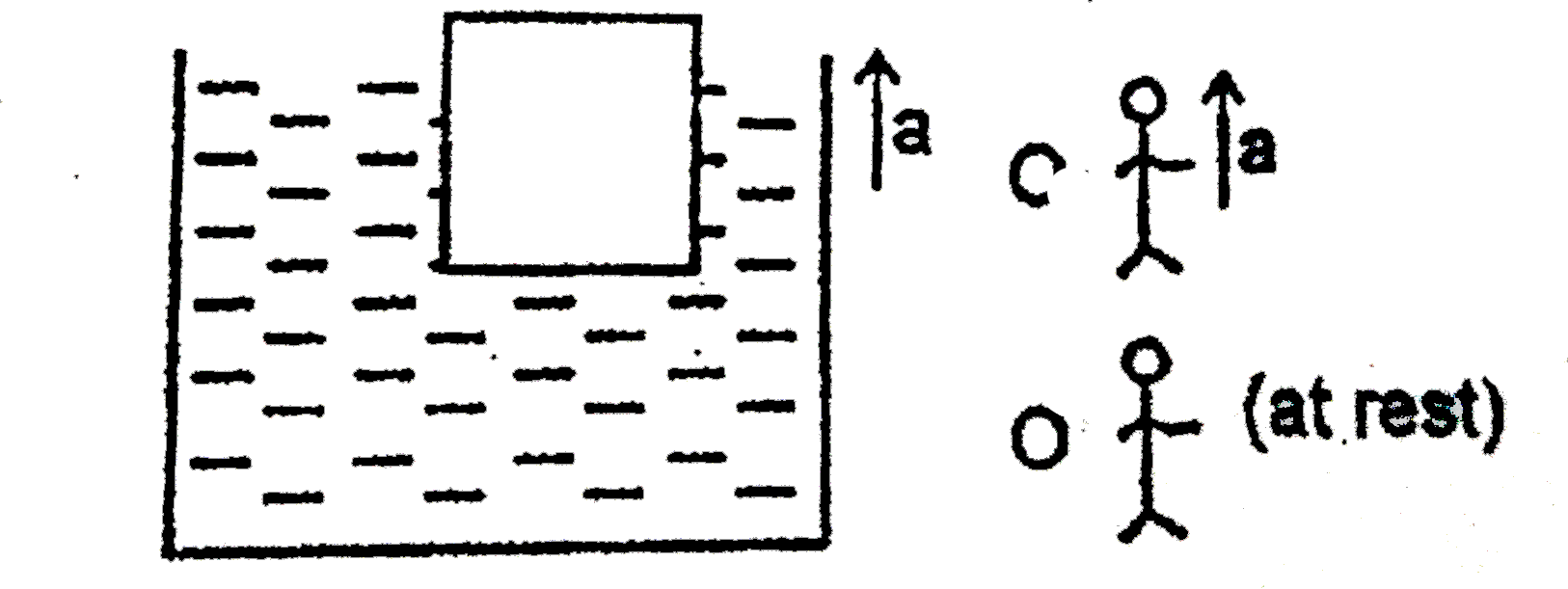
View Solution_S01_025_Q01.png)
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood `=800kg//m^(3)` and spring constant of the spring `=50N//m`. Take `g=10m//s^(2)`
View SolutionA large block of ice cuboid of edge length 'l' and density `rho_(ice) -0.9 rho_(w)`, has a larger vertical hole along its axis. This block is floating in a lake. Find out length of the rope required to raise a bucket of water through the hole.
View SolutionFor a fluid which is flowing steadily, the level in the vertical tubes is best represented by
View SolutionA cylindrical wooden float whose base area S and the height H drift on the water surface. Density of wood d and density of water is `rho`. What minimum work must be performed to take the float out of the water ?
View SolutionA circular cylinder of height `h_(0)=10 cm ` and radius `r_(0)`=2 cm is opened at the top and filled with liquid. It is rotated about its vertical axis. Determine the speed of rotation so that half the area of the bottom gets exposed (`g=10 m//s^(2)`):
View SolutionWater flows ina horizontla tube as shown in figure. The pressure of water changes by 600 N m^-2 between A and B whre the areas of cross section asre `30cm^2 and 15cm^2 respectively. Find the rate of flow of water through the tube.
 ,
,
View SolutionThe cubical container ABCDEFGH which is completely filled with an ideal (nonviscous and incompressible) fluid, moves in a gravity free space with a acceleration of `a=a_0 (hat i -hatj +hat k)` where `a_0` is a positive constant. Then the minimum pressure at the point will be
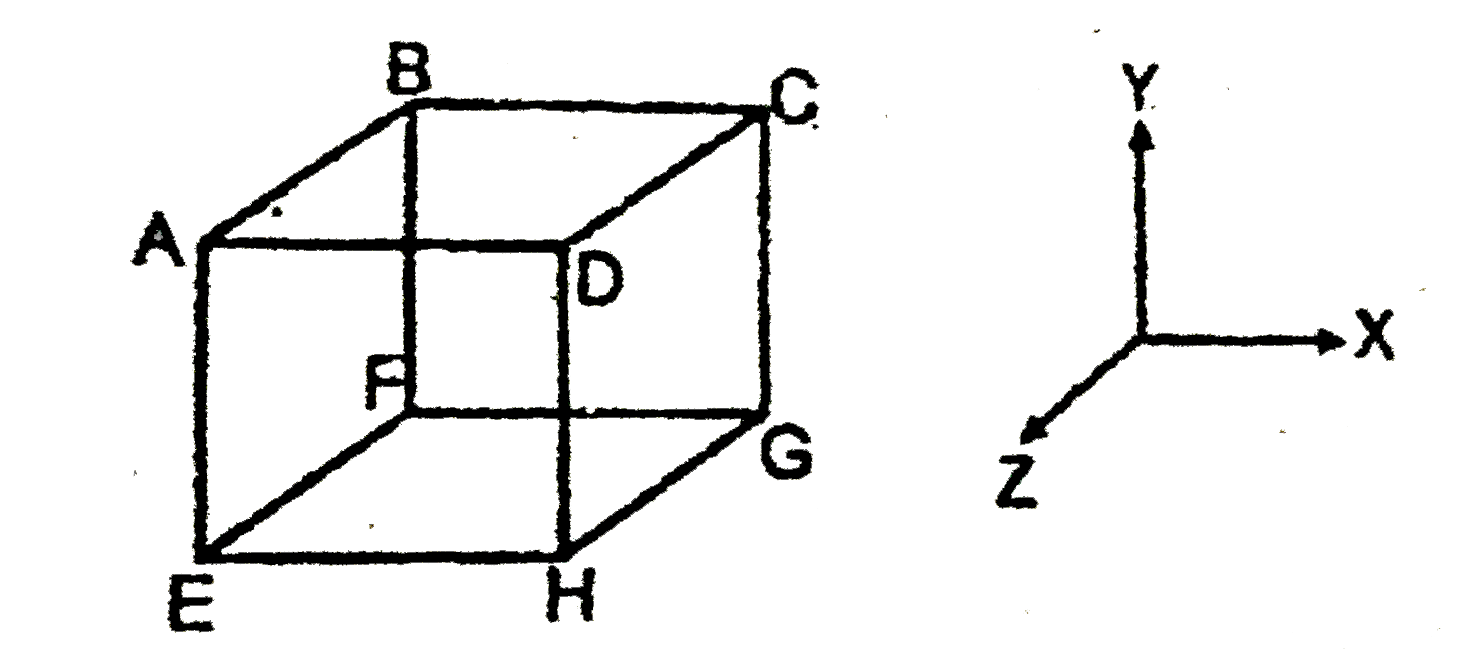
View SolutionTo measure the atmospheric pressure, four different tubes of length 1m, 2m , 3m and 4m are used. If the height of the mercury column in the tubes is `h_(1),h_(2),h_(3),h_(4)` respectively in the four cases, then `h_(1):h_(2):h_(3):h_(4)`
View SolutionAn open tank `10 m` long and `2 m` deep is filled up to `1.5 m` height of oil of specific gravity `0.82`. The tank is uniformly accelerated along its length from rest to a speed of `20 m//s` horizontally. The shortest time in which the speed may be attained without spilling any oil is
View Solution_S01_083_Q01.png)
Water (density `rho`) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at `3.27m//s^(2)` in the direction of its length determine the depth of water at each end of tank.
View Solution_S01_020_Q01.png)
In a given U-tube (open at one-end) find out relation between p and `p_(a)`
Given `d_(2)=2xx13.6gm//cm^(3),d_(1)=13.6gm//cm^(3)`
View SolutionOne end of a long iron chain of linear mass density `lambda` is fixed to a sphere of mass m and specific density 1/3 while the other end is free. The sphere along with the chain is immersed in a deep lake. If specific density of iron is 7 , the height h above the bed of the lake at which the sphere will float in equilibrium is (assume that the part of the chain lying on the bottom of the lake exerts negligible force on the upper part of the the chain)

View Solution
Numberical MCQ single questions and complete solutions for chapter FLUID MECHANICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11