Complete Solutions to Unsolved Numerical Problems of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| PHYSICS GALAXY | Unsolved Numerical Problems |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
A block of wood floats in water two-thirds of its volume submerged. In oil the block of floats with 0.90 of its volume submerged. Find the density of (a) wood and (b) oil, if density of water I `10^(3) kg//m^(3)`.
View SolutionA balloon filled with hydrogen has a volume of `1m^(3)` and its mass is `1kg`. What would be the volume of the block of a very light material which it can just lift ?
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is `10cm^2`, the water velocity is `1ms^-1` and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is `5cm^2`, is........Pa. (Density of water `=10^3kg.m^-3`)
View SolutionA glass tube of radius `0.8 cm` floats vertical in water, as shown in figure. What mass of lead pellets would cause the tube to sink a further`3 cm`?
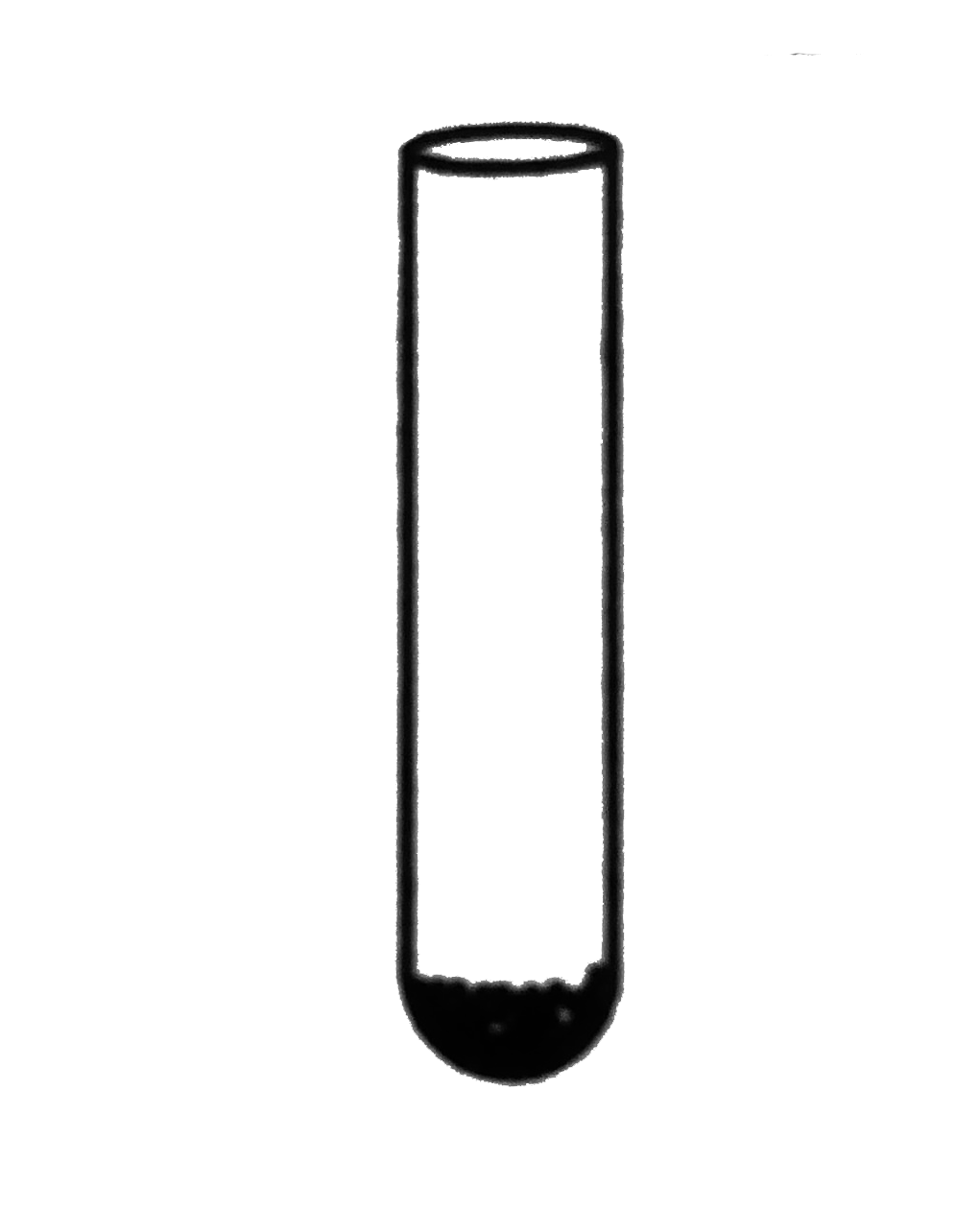
View SolutionWhen equal volumes of two substances are mixed together, the specific gravity of the mixture is 5. But when equal weights of the same substance are mixed together, the specific gravity of the two is 3. Find the specific gravity of two substances.
View SolutionWater from a tap emerges vertically downwards with an initial spped of `1.0ms^-1`. The cross-sectional area of the tap is `10^-4m^2`. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The cross-sectional area of the stream 0.15 m below the tap is
View SolutionA piece of metal floats on mercury. The coefficient of volume expansion of metal and mercury are `gamma_1 and gamma_2`, respectively. if the temperature of both mercury and metal are increased by an amount `Delta T`, by what factor does the fraction of the volume of the metal submerged in mercury changes ?
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density `0.85 g//cm^3` The pressure at the bottom of the tank, due to these liquids is
View SolutionA stone of density `2.5 g//cm^(3)` completely immersed in sea water is allowed to sink from rest. Calculate the depth to which the stone would sink in two seconds. Neglect the effect of friction. Specific gravity of sea water is 1.025 and acceleration due to gravity is `9.8 m//s^(2)`.
View SolutionA cube of wood supporting 200gm mass just floats in water. When the mass is removed, the cube ruses by 2cm. What is the size of the cube?
View SolutionWater is flowing continuously from a tap having an internal diameter `8xx10^(-3)`m. The water velocity as it leves the tap is `0.4 ms^(-1)`. The diameter of the water stream at a distance `2xx10^(-1)`m below the tap is close to `(g=10m//s^(2))`
View SolutionA certain block weighs 15 N in air. But is weighs only 12 N when completely immersed in water. When immersed completely in another liquid, it weighs 13 N. Calculate the relative density of (i) the block and (ii) the liquid.
View SolutionA cylindrical tank `1 m` in radius rests on a platform `5 m` high. Initially the tank is filled with water to a height of `5 m`. A plug whose area is `10 ^-4 m^2`, is removed from an orifice on the side of the tank at the bottom. Calculate the following :
(a) Initial speed with which the water flows from the orifice.
(b) Initial speed with which the water strikes the ground,
( c) Time taken to empty the tank to half its original value.
View Solution`A` vertical uniform `U` tube open at both ends contains mercury. Water is poured in one limb until the level of mercury is depressed `2cm` in that limb. What is the length of water column when this happens.
View SolutionA piece of copper having an internal cavity weights 264 g in air and 221 g in water. Find the volume of the cavity. Density of copper is `8.8 g//cm^(3)`
View SolutionA beaker of mass 1 kg contains 2 kg of water and rests on a scale. A 2kg block of aluminum (specific gravity 2.70) suspended from a spring scale is suspended from a spring scale is submerged in water, as shown in figure. Find the readings of both scales.
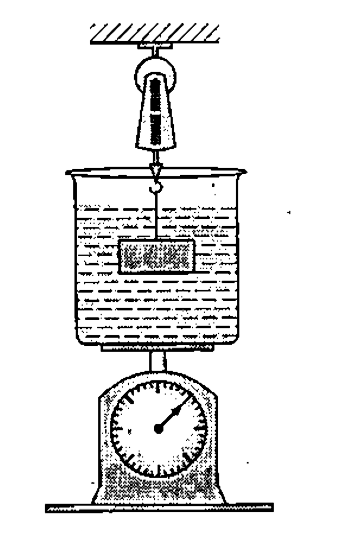
View SolutionA Piece of brass (alloy of zinc and copper) weighs 12.9 g in air. When completely immersed in water it weighs 11.3 g . What is the mass of copper contained in the alloy ? Specific gravity of zinc and copper are 7.1 and 8.9 respectively.
View SolutionShows a hydraulic press with the larger piston of diameter `35cm` at a height of `1.5 m` relative to the smaller piston of diameter `10cm.` The mass on the smaller piston is `20gk.` What is the force exerted on the load by the lerger piston ? The density of oil in the press is `750 "kgm"^(-3).`
View SolutionTwo identical cyclindrical vessels (area of cross section `3.5 xx 10^(-3) m^(2)`) with their bases at the same level contain liquid of density `800 kg//m^(3)`. The height of liquid in one vessel is 0.3 m and in the other it is `0.1 m`. Assuming `g = 10 m//s^(2)`, find the workdone by gravity in equalising levels when the vessels are interconnected at bottom.
View SolutionAn open cubical tank completely filled with water is kept on a horizontal surface. Its acceleration is then slowly increasesd to `2m//s^(2)` as shown in the figure. The side of the tank is 1m. Find the mass of water that would spill out of the tank.

View SolutionA vertical U-tube of uniform inner cross-section contains mercury in both of its arms. A glycerine `("density" 1.3 "gcm"^(-3))` column of length `10 cm `is introduced into one of the arms Oil of density `0.8 "gcm"^(-3)` is poured in the other arm until the upper surface of the oil and glycerine are in the same horizontal level. Find the length of the oil column.
View SolutionWater flows through the tubes shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are `5 cm^(2)` and `2 cm^(2)` respectively. The rate of flow of water through the tube is `500 cm^(3)//s`. Find the difference of mercury levels in the U-tube.
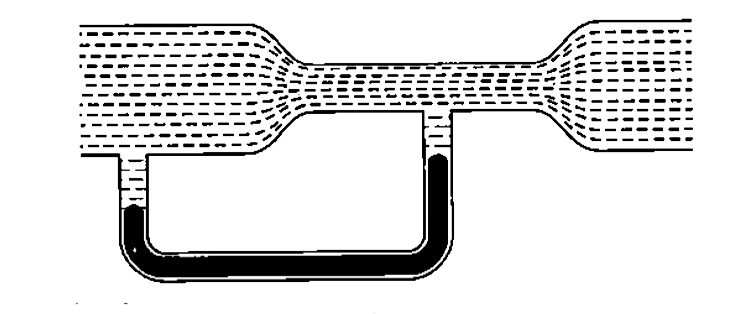
View SolutionA person can change the volume of his body by taking air into his lungs. The amount of change can be determined by weighing the person under water. Suppose that under water a person weighs 20.0 N with partially full lungs and 40.0 N with empty lungs. Find the change in body volume.
View SolutionA vessel contains oil (density `=13.6 gm//cm^3`). A uniform sphere floats with half its volume immersed in mercury and the other half in oil. The density of the material of sphere in `gm//cm^3` is:
View SolutionThe tension in a string holding a solid block below the surface of a liquid (of density greater than that of solid) as shown in figure is `T_(0)` when the system is at rest. What will be the tension in the string if the system has an upward acceleration a?
 .
.
View SolutionA J-tube, shown in figure, contains a volume V of dry air trapped in arm A of the tube. The atmoshpere pressure is H cm of mercury. When more mercury is poured in arm B, the volume of the enclosed air and its pressure changes. What should be the difference in mercury levels in the two arms so as to reduce the volume of air 1/2.
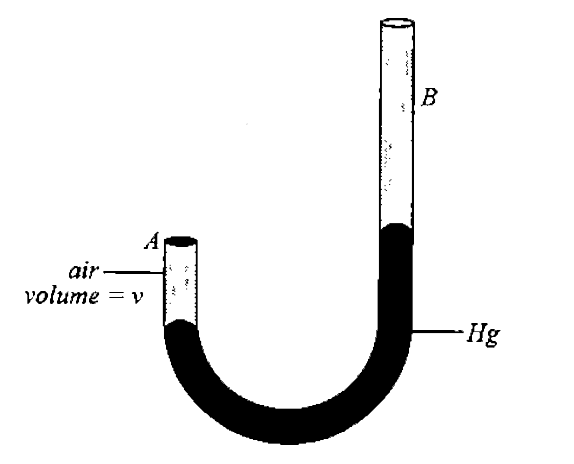
View SolutionA block of ice with an area A and a height h floats in water of density `rho_(0)`. What work should be performed to submerge the ice block completely into water if density of ice is `rho_(1)` ?
View SolutionA solid ball of density half that of water falls freely under gravity from a height of 19.6 m and then enters water. Upto what depth will the ball go? How much time will take to come again to the water surface? Neglect air resistance and viscosity effects in water `(g = 9.8 m//s^(2))`
View SolutionA U-tube containing a liquid is accelerated horizontally with a constant acceleration `a_0`. If the separation between the vertical limbs is l find the difference in the heights of the liquid in the two arms.
View SolutionThe tank in figure discharges water at constant rate for all water levels above the air inlet R. Find the height above datum to which water would rise in the manometer tubes M and N.

View SolutionThe time period of a sample pendulum is T. Now the bob is immersed in a liquid of density `sigma`. If density of material of bob is `rho`, what will be the time period of the pendulum.
View SolutionA rubber ball of mass m and radius r is submerged in water to a depth h and released. What height will the ball jump up to above the surface of the water? Neglect ther resistance of water and air. Take water density `rho`.
View SolutionA cubical vessel of height `1` m is full of water. What is the workdone in pumping water out of the vessel?
View SolutionA tank is filled with water to a height H. A hole is punched in the wall at a depth h below the water surface. Find the distance x from the wall at which the stream strikes the floor. Could a hole be punched at another depth so that this second stream would have the same range? If so at what depth? For what value of h is range maximum?
View SolutionA large block of ice `5 m` thick has a vertical hole drilled through it and is floating in the middle of a lake. What is the minimum length of a rope required to scoop up a bucket full of water through the hole? Relative density of ice `=0.9`.

View SolutionA rectangular container of water undergoes constant acceleration down an incline as shown in figure. Determine the slope `tan theta` of the free surface using the coordinate system shown. Take `g = 10m//s^(2)`

View SolutionAn iron casting containing a number of cavities weight `6000N` in air and `4000N` in water. What is the volume of the cavities in the casting? Density of iron is `7.87g//cm^(3)`. Take `g = 9.8 m//s^(2)` and density of water `= 10^(3) kg//m^(3)`.
View SolutionA uniform rod of length b capable of tuning about its end which is out of water, rests inclined to the vertical. If its specific gravity is 5/9, find the length immersed in water.
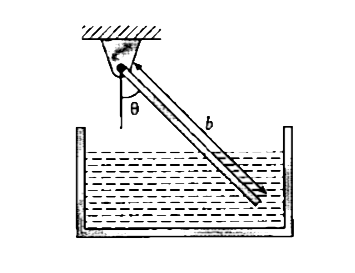
View Solution_S01_025_Q01.png)
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood `=800kg//m^(3)` and spring constant of the spring `=50N//m`. Take `g=10m//s^(2)`
View SolutionA tank is filled with a liquid upto a height H, A small hole is made at the bottom of this tank Let `t_(1)` be the time taken to empty first half of the tank and `t_(2)` time taken to empty rest half of the tank then find `(t_(1))/(t_(2))`
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height `H//2`. The lower density liquid is open to the atmoshpere having pressure `P_(0)`. A homogeneous solid cylinder of length `L(L lt H//2)` corss-sectional area `A//5` is immersed such that it floats with its axis vertical at the liquid interface with the length `L//4` in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
View SolutionIn the arrangement shown in figure a viscous liquid whose density is `1gm//cm^(3)` flows along a tube out of a wide tank A. Find the velocity of the liquid flow if `h_(1) = 10 cm, h_(2) = 20 cm, h_(3) = 35 cm`. All the distances l are equal.

View SolutionA block of wood weighs 12 kg and has a relative density 0.6. It is to be in water with 0.9 of its volume immersed. What weight of a metal is needed (a) if the metal is on the top of wood, (b) if the metal is attached below the wood? [RD of metal =14]
View SolutionA level controller is shown in the figure it contains of a thin circular plug of diameter 10 cm and a cyclindrical plug of diameter 20 cm tied together with a light rigid rod of length 10 cm. The plug fits in smoothly in a dram hole at the bottom of the tank which opens into atmosphere. As water fills up and the level reaches height h, the plug opens. Find h. Determine the level of water in the tank when the plug closes again. The float has a mass 3kg and the plug may be assumed as massless.

View SolutionTwo communicating cylindrical tubes contain mercury. The diametr of one vessel is four times large than the diameter of the outer. A column of water of heigt `70 cm` is poured into the narrow vessel. How much wil the mercury level rise in the other vessel and how much will it sink in the narow one? How much will the mercury level rise in the narrow vessel, if a column of water of the same height is pured into the broad vessel?

View SolutionThe U-tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend. Given atmospheric pressure `=1.01xx 10^(5)N//m^(2),g=9.8 m//s^(2)` and density of water `=10^(3)kg//m^(3)`
 .
.
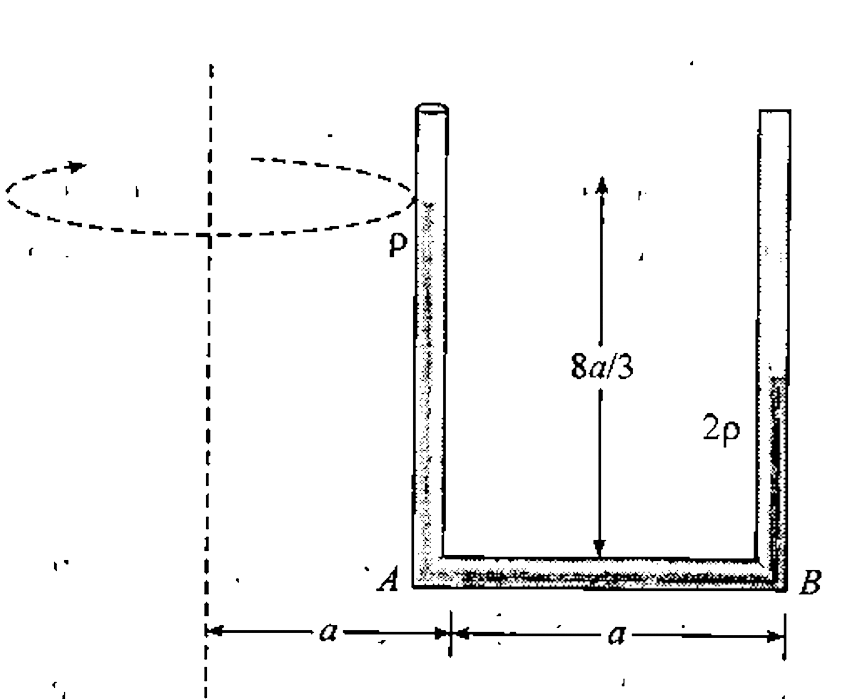
View SolutionThe interface of two liauids of densities `rho` and `2rho` respectively lies at the point A in a U tube at rest. The height of liquid columb above A is `8a//3` where AB = a. The cross-sectional area of the tube is S. With what angular velocity the tube must be whirled about a vertical axis at a distance 'a' such that the interface of the liquids shifts towards B by `2a//3`.
View SolutionA wooden stick of length `L`, radius `R` and density `rho` has a small metal piece of mass `m` ( of negligible volume) attached to its one end. Find the minimum value for the mass `m` (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density `sigma(gtrho)`.
View SolutionA container of large uniform cross sectional area `A`, resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density `d` and `2d`, each of height `H/2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`. A tiny hole of area `(s(sltltA)` is punched on the vertical side of the container at a height `h(hltH/2)`. Determine

a.the initial speed of efflux of the liquid at the hole
b. the horizontal disance `x` travelled by the liquid initially
c. the height `h_m` at which at the hole should be punched so that the liquid travels the maximum distance `x_(m)` initially. also calculate `x_(m)` (neglect air resistance in calculations).
View SolutionA small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities are`rho` and `sigma(rhogtsigma)` fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
View SolutionA rectangular air mattress has a length 2.0 m, a width 0.50 m and thickness can float on water if the mass of the mattress is 2.0 kg. what is the density of the mattress ?
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end of the bottom of tank as shown in figure. The tank is filled with water upto a height of `0.5 m`. Find the angle `theta` that the plank makes with the vertical in the equilibrium position. [Exclude the case `thea = 0`]

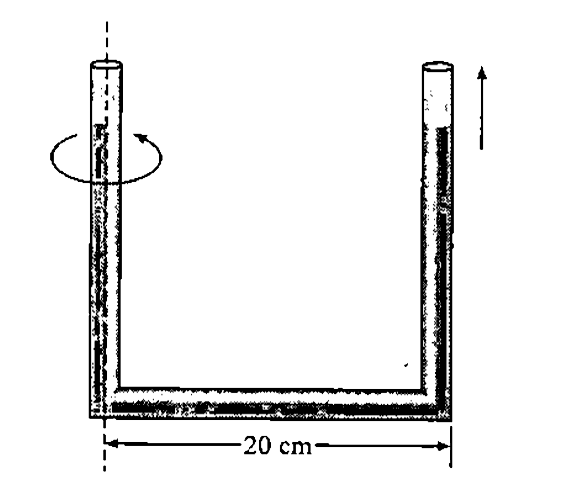
View SolutionThe cross-sectional area of the U-tube shown in the figure is everywhere uniform and of value `1.25 xx 10^(-3)m^(2)`. The horizontal section of the tube is of length 20 cm. When at rest, the limbs of the tube contain a liquid of density 2.5 up to equal heights. If the tube is rotated with angular velocity of `8.4 rad//s` about one limb, calculate the volume of liquid that flows from one limb to the other.
View SolutionCalculate the rate of flow of glycerine of density `1.25 xx 10^(3) kg//m^(3)` through the conical section of a pipe if the radii of its ends are 0.1m and 0.04 m and the pressure drop across its lengths is `10N//m^(2)`.
View SolutionAn ice cube of edge a is placed in an empty cylindrical vessel of radius 2a. Find the edge (in cm) of ice cube when it just leaves the contact with the bottom assuming that ice melts uniformly maintaining its cubical shape. Take a = 12 `pi` cm (Ice is lighter than water)
View SolutionA cylindrical tank having cross-sectional area `A = 0.5 m^(2)` is filled with two liquids of density `rho_(1)=900 kg m^(-3)` and `rho_(2)=600 kgm^(-3)`, to a height `h=60cm` each as shown in the figure. A small hole having area `a=5cm^(2)` is made in right vertical wall at a height `y = 20 cm` from the bottom. A horizontal force `F` is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (`ake `g = 10 ms^(-2)`).
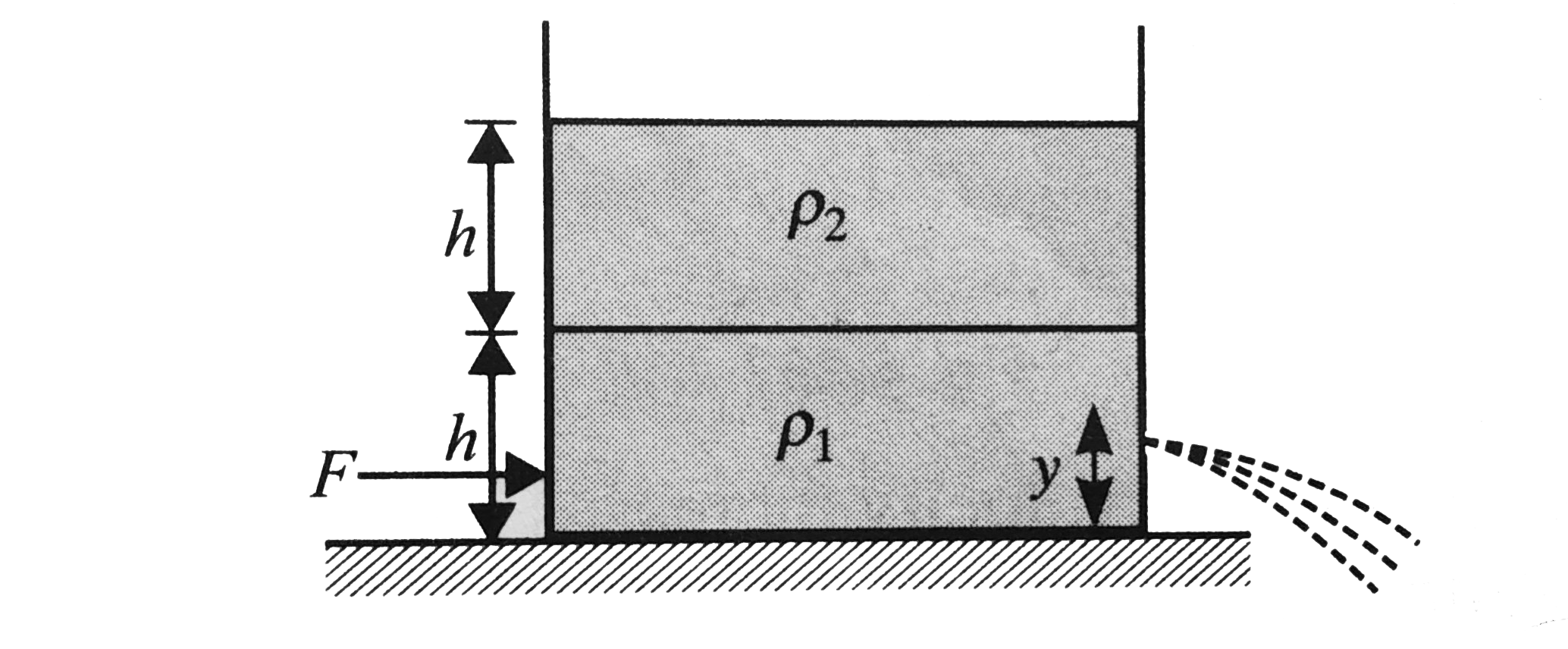
The horizontal force required to keep the cylinder in static equilibrium, on a smooth horizontal plane is
View SolutionA conical vessel wihout a bottom stands on a table. A liquid is poured with the vessel & as soon as the level reaches h, the pressure of the liquid raises the vessel. The radius of the base of the vessel is R and half angle of the cone `alpha` and the weight of the vessel is W. What is the density of the liquid ?

View SolutionWater flows in a horizontal pipe whose one end is closed with a value and the pressure gauge falls to `1 xx 10^(5)N//m^(2)` when the value is opend. Calculate the speed of water flowing in the pipe.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is ` 0.05 m` and the speed of rotation is `2 rev//s`, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA cylinder tank of base area A has a small hole of areal a at the bottom. At time `t=0`, a tap starts to supply water into the tank at a constant rate `alpha m^(3)//s`.
(a) What is the maximum level of water `h_(max)`in the tank?
(b) find the time when level of water becomes `h(lt h_(max))`.
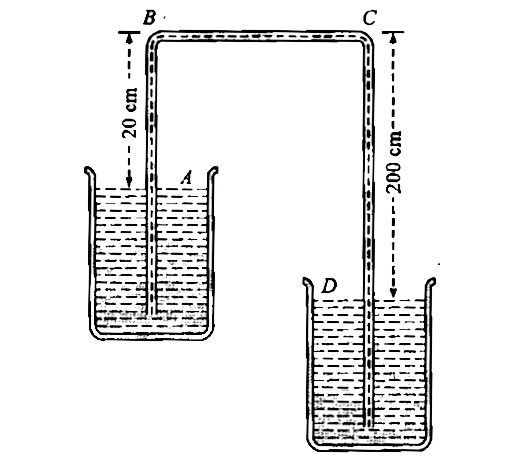
View SolutionThe figure shows a siphon in action. The liquid flowing through the siphon has a density of `1.5 gm//cm^(3)`. Calculate the pressure difference between
(a) Points A and D,
(b) Points B and C
View SolutionA water clock used in ancient Greek is designed as a closed vessel with a small orifice O. The time is determined accrding to the level of the water in the vessel. What should be the shape of the vessel be for the time scale to be uniform. Find mathemtical equation governing curve AOB.
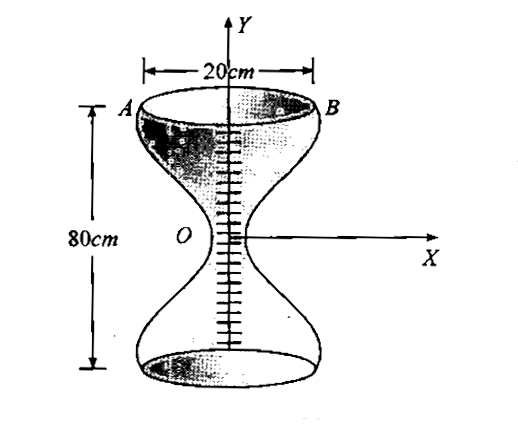
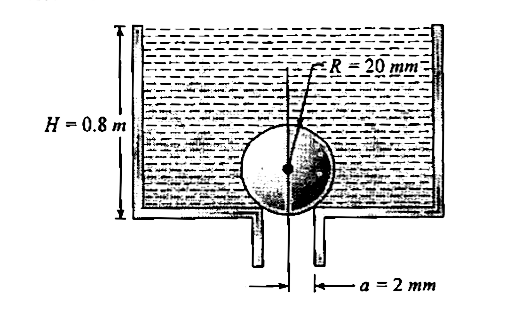
View SolutionA sphere of radius R, made from material of specific gravity SG, is submerged in a tank of water. The sphere is placed over a hole, of radius a, in the tank bottom. For the dimensions given, determine the minimum SG required for the sphere to remain in the position shown.
View SolutionTwo identical container are open at the top and are connected at the bottom via a tube of negligible volume and a valve which is closed. Bith containers are filled initially to the same height 1.00m, one with water the other with mercury, as the drawing indicates. The valve is then opened. Water and mercury are immiscible. Determine the fluid level in the left container when equilibrium is re-established.

View SolutionA thin rod of length (L) and area of cross - section (S) is pivoted at its lowest point (P) inside a stationary, homegeneous and non - viscous liquid. The rod is free to ratate in a vertical plane about a horizontal axis passing through (P). The density (d_1) of the material of the rod is smaller than the density (d_2) of the liquid. The rod is displaced by a small angle (theta) from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
 .
.
View SolutionConsider a horizontally oriented syringe containing water locate at a height of `1.25 m` above the ground. The diameter of the plunger is `8 mm` and the diameter of the nozzle is `2 mm`. The plunger is pushed with a constant speed of `0.25m//s.` Find the horizontal range of water stream on the grond. Take `g=10 m//s^(2)`

View SolutionA water pipe with interna diameter of 2m carries water at the floor of a house with velocity 2 m/s and at pressure `2 xx 10^(5) N//m^(2)`. Another pipe of internal diameter 1 cm is connected to it and takes water to 1 st floor, 5m above ground. What is the velocity and water pressure at 1st floor ? (Take `g = 10 m//s^(2)`).
View SolutionWater and oil are poured into the two limbs of a U-tube containig mercury. The interface of the mercury and the liquids are at the same height in both limbs.
Determine the height of the water column`h_(1)` if that of the oil `h_(2)=20cm`. The density of the oil is `0.9`.
 .
.
View SolutionPure water is added drop by drop to a vessel of volume V filled with a salt solution of specific gravity `gamma` which is allowed to overflow. Find the specific gravity of the solution when a volume U of water hs been poured.
View SolutionWater flows out of a big tank along a tube bent at right angles, the inside of the tube is of radius `r`. The length of the horizontal portion is `l`. The rate of water flow is `Q`. Find the moment of reaction forces of flowing water, acting on the tube walls relative to point `O`.
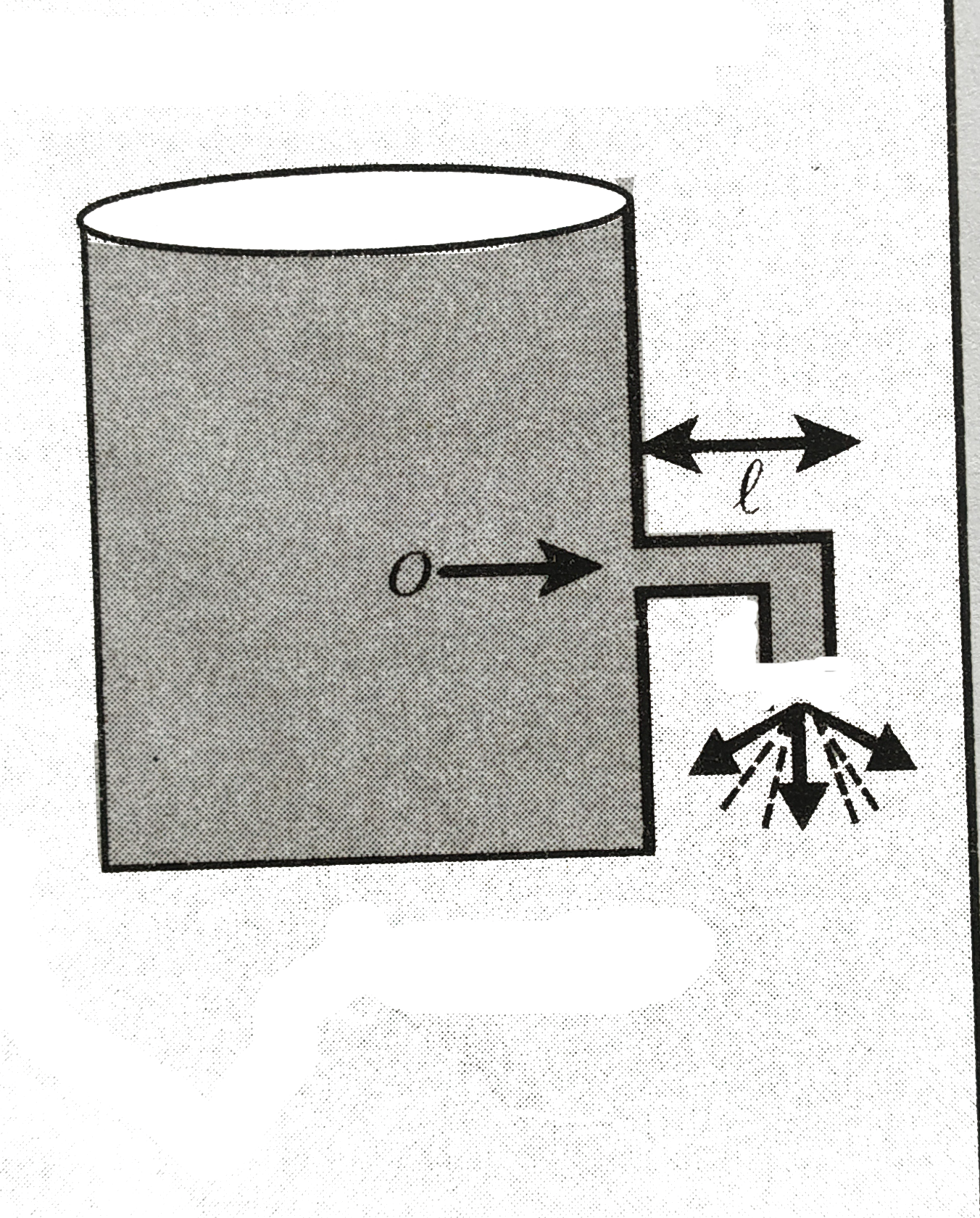
View SolutionA cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is `(1//400)` that of the vessel.
(a) What is the tiome required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
View SolutionAn open reactangular tank with tank with dimensions `5xx4mxx3m` contains water upto a height of 2m is accelerated horizontally along the longer life.
(a) Determine the maximum acceleration that can be given without spilling the water.
(b) If this acceleration is inscreased by `20%`. Calculate the percentage of water spilt over.
(c) If initially,the tank is closed at the top and is accelerated horizontally by `9m//s^(2)`,find the gauge pressure at the bottom of the front and rear walls of the tank. `(g=10m//s^(2))`

View SolutionTwo holes, each of area `A = 0.2 cm^(2)` are drilled in the wall of a vessel filled with water. The distances of the holes from the level of water are h and `h + H`. Find the point where the streams flowing out of the holes intersect. The level of water is maintained in the vessel by regulated supply.
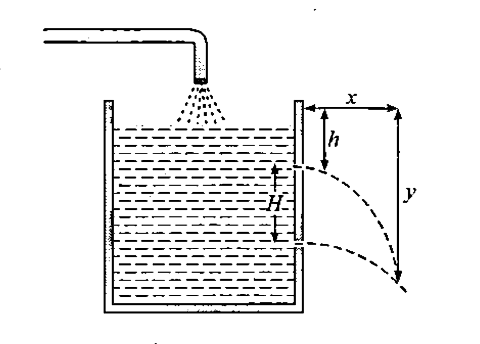
View SolutionA vertical tube has diameter 0.016 m at its bottom end from which water flows out at the rate of 1.2 kg per minute. The pressure at the end is atmospheric pressure 0.7 m of mercury. If the diameter of the tube is 0.004 m at a height of 0.3 m from the bottom end, fidn the pressure there.
View SolutionA cylinderical tank of height 0.4 m is open at the top and has a diameter 0.16m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius `5 xx 10^(-3)m` in its bottom.
View SolutionA large open top container of negligible mass and uniform cross sectional area `A` a has a small hole of cross sectional area `A//100` in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density `rho` and mass `M_(0)`. Assuming that the liquid starts flowing out horizontally through the hole at `t=0`, calculate a the acceleration of the container and b its velocity when `75%` of the liquid has drained out.
View SolutionA cylindrical bucket, open at the top, is 0.200 m high and 0.100 m in diameter. A circular hole wih cross-section area `1.00 cm^(2)` is cut in the centre of the bottom of the bucket. Water flows into the bucket from a tube above it at the rate of `1.30xx10^(-4) m^(3)//s`. How high will the water in the bucket rise?
View SolutionA uniform cylindrical block of length `l` density `d_(1)` and area of cross section A floats in a liquid of density `d_(2)` contained in a vessel `(d_(2) gt d_(1))`. The bottom of the cylinder just rests on a spring of contant k. The other end of the spring is fixed to the bottom of the vessel. A weight that may be placed on top of the cylinder such that the cylinder is just submerged in the liquid. find the weight.
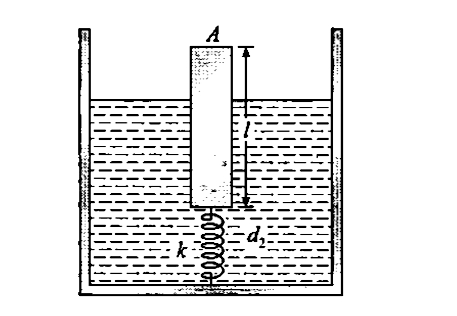
View SolutionA ball of density d is dropped on to a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time `t_1`. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density of `d_L`
(a) If `dltd_L`, obtain an expression (in terms of d, `t_1` and `d_L`) for the time `t_2` the ball takes to come back to the position from which it was released.
(b) Is the motion of the ball simple harmonic?
(c) If `d=d_L`, how does the speed of the ball depend on its depth inside the liquid? Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.
View SolutionA side wall of a wide open tank is provided with a narrowing tube through which water flows out. The cross-sectional area of the tube decreases from `S=3.0 cm^(2)` to `s=1.0 cm^(2)`. The water level in the tank is `h=4.6 m` heigher than in the tube. Neglecting the viscosity of water, find the horizontal component of the force tending to pull the tube out of the tank.
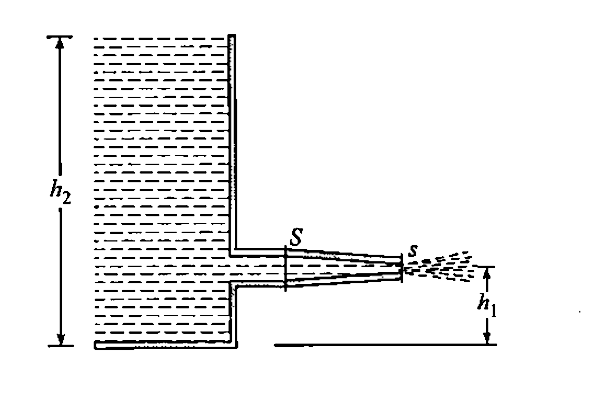
View SolutionA ping-pong ball has a volume V and density `(1//10)` th of water. What force would be required to hold it completely submerged under water?
View SolutionWater leaks out from an open tank through a hole of area `2mm^2` in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tankis `0.4 m^2`. The pressure at the open surface and the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. a. Find the initial speed of water coming out of the hole. b. Findteh speed of water coming out when half of water has leaked out. c. Find the volume of water leaked out during a time interval dt after the height remained is h. Thus find the decrease in height dh in term of h and dt.
d. From the result of part c. find the time required for half of the water to leak out.
View SolutionA steel ball floats in a vessel with mercury. How will be volume of the part of the ball submerged in mercury change if a layer of water completely covering the ball is poured above the mercury? If `rho_(w), rho_(s)` and `rho_(m)` are the densities of water, steel and mercury, find the ratio of these two volumes in terms in of `rho_(w), rho_(s)` and `rho_(m)`.
View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are `1cm^2 and 0.5 cm^2` respectively. The height difference between A and B is 5m. If the speed of water at A is 10 `cms^-1` find a the speed at B and b the difference in pressures at A and B.

View SolutionA jet of water issues vertically at a speed of 0.1 square inch cross-section. A ball weighing one pound is balance in the air by impact of water on its underside. Find the height of the ball above the level of jet. Take `g=3 ft//s^(2)`
View Solution
Unsolved Numerical Problems questions and complete solutions for chapter FLUID MECHANICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11