Complete Solutions to Multiple choice questions. of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMODYNAMICS |
| PRADEEP | Multiple choice questions. |
| Number Of Questions | 96 |
| Academic Year | 2023-24 |
Consider a heat engine as shown in (figure). `Q_(1) and Q_(2)` are heat added to heat bath `T_(1)` and heat taken from `T_(2)` one cycle of engine. `W` is the mechanical work done on the engine.
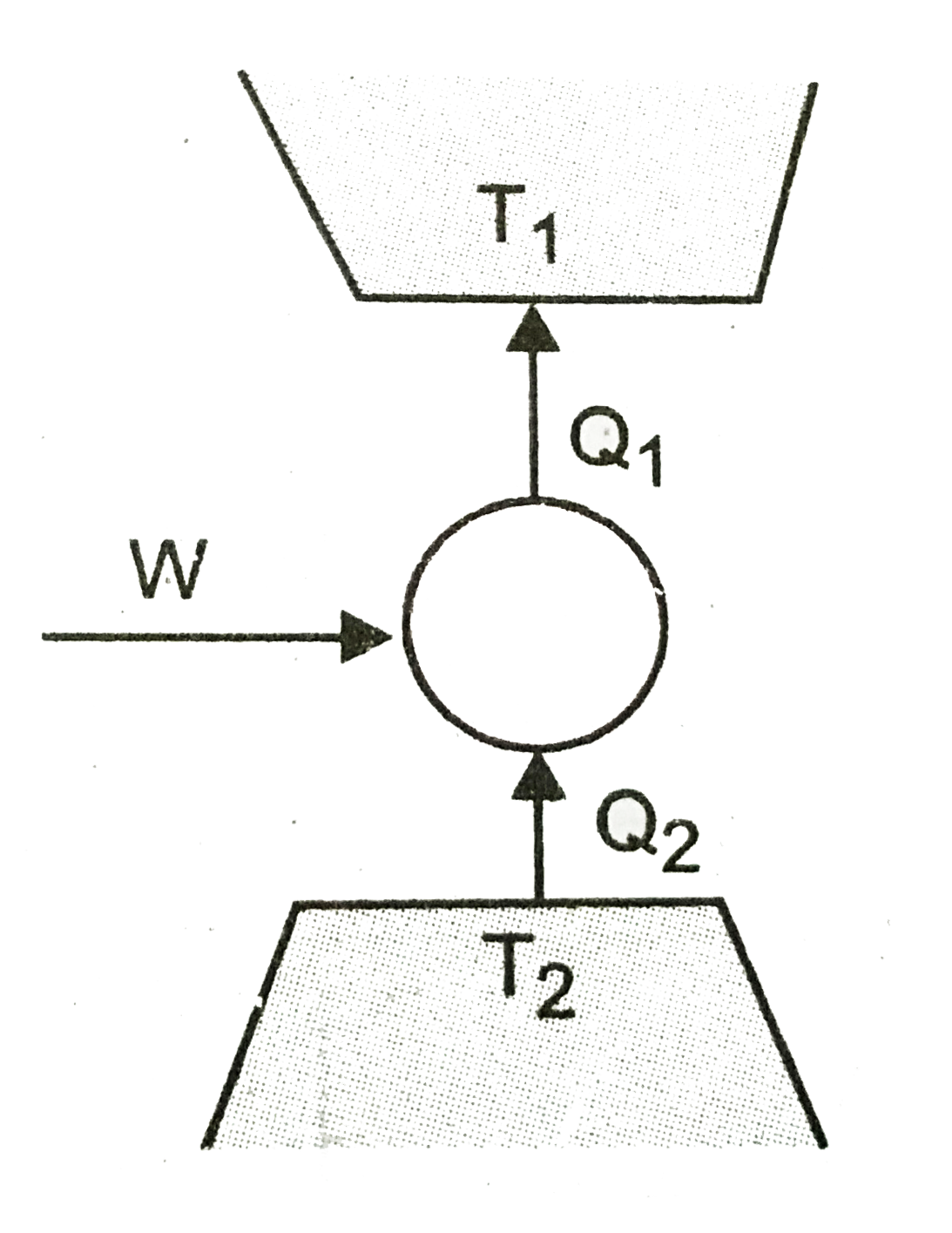
If `Wgt0`, then possibillities are:
View SolutionConsider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is
View SolutionConsider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume `u=U/V propT^4` and pressure `P=1/3(U/V)`. If the shell now undergoes an adiabatic expansion the relation between T and R is :
View SolutionWhich of the following `P-V` diagrams best represents an isothermal process?
View SolutionThe pressure of a gas is increased by `50%` at constant temperature. The decrease in volume will be nearest to
View SolutionA thermodynamic system undergoes cyclic process `ABCDA` as shown in figure. The work done by the system is
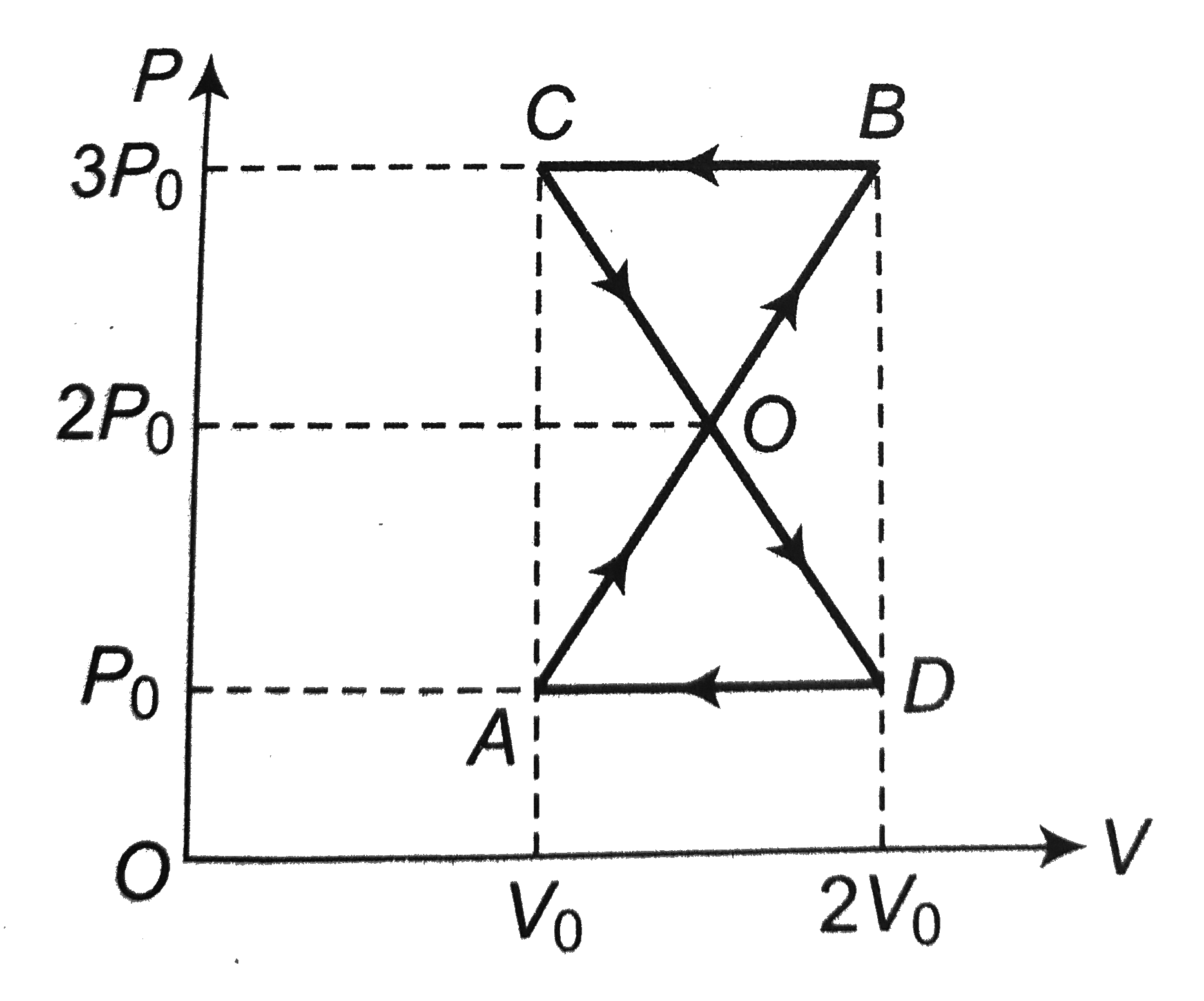
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is `(gamma=3//5)`
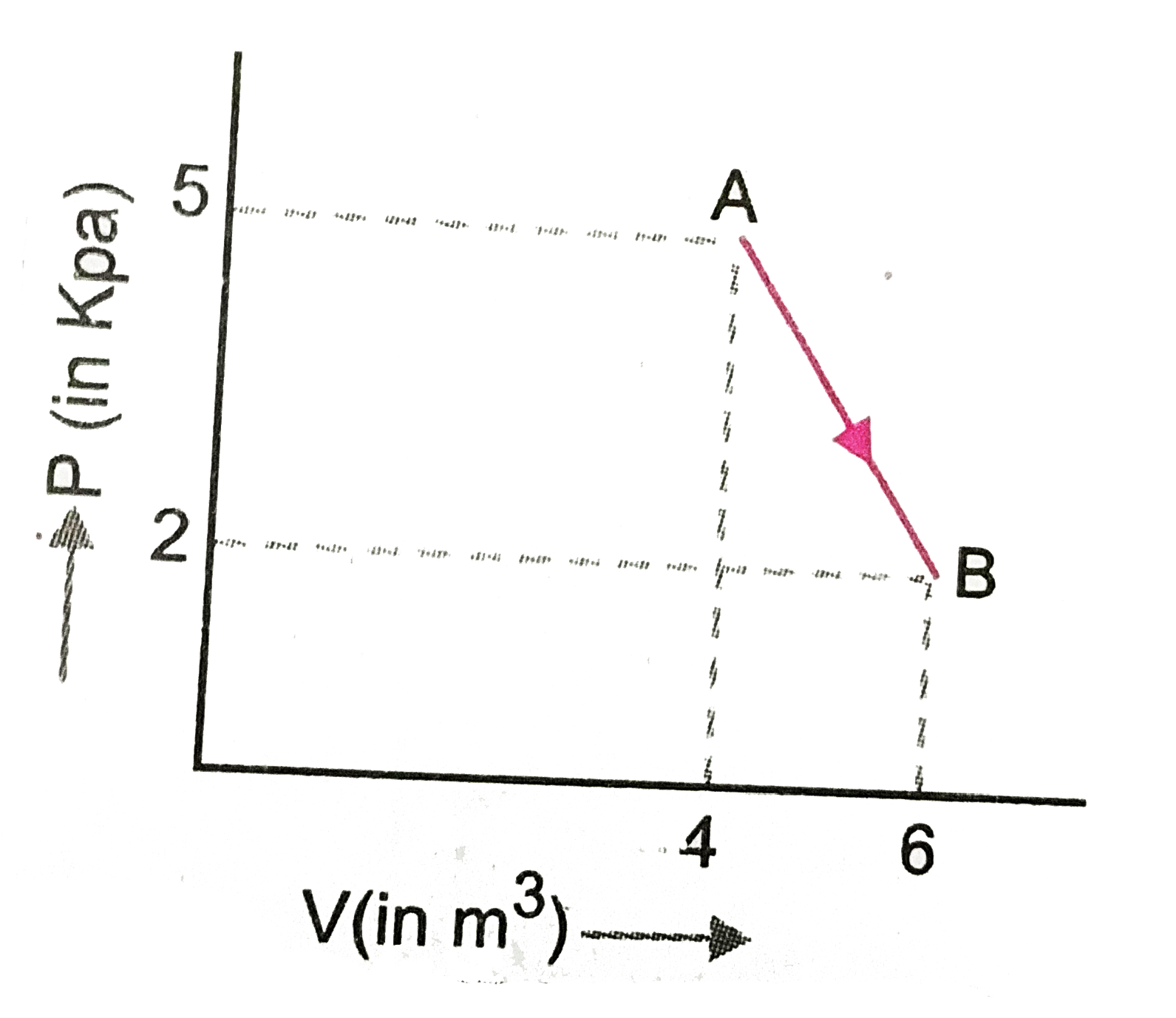
View SolutionAt `27^@C` two moles of an ideal monoatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate (i) the final temperature of the gas, (ii) change in its internal energy, and (iii) the work done by the gas during this process.
View SolutionIn the above question, change in internal energy of gas is
View Solution`400 c c` volume of gas having `gamma=5/2` is suddenly compressed to `100 c c`. If the initial pressure is `P`, the final pressure will be
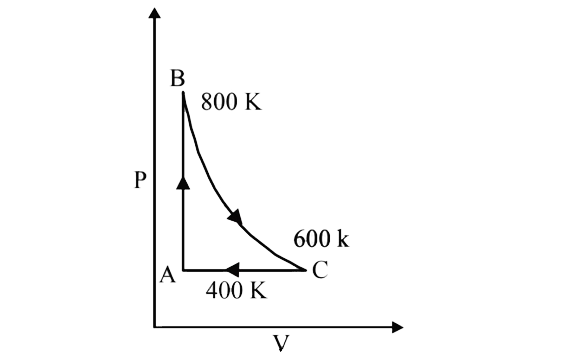
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
View SolutionA thermodynamic system is taken from an initial state I with internal energy `U_i=-100J` to the final state f along two different paths iaf and ibf, as schematically shown in the figure. The work done by the system along the pat af, ib and bf are `W_(af)=200J, W_(ib)=50J and W_(bf)=100J` respectively. The heat supplied to the system along the path iaf, ib and bf are `Q_(iaf), Q_(ib),Q_(bf)` respectively. If the internal energy of the system in the state b is `U_b=200J and Q_(iaf)=500J`, The ratio `(Q_(bf))/(Q_(ib))` is

View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_P//C_V` for the gas is
View SolutionStarting with the same initial conditions, an ideal gas expands from volume `V_1 to V_2` in three different ways. The work done by the gas is W_1 if the process is purely isothermal, `W_2`if purely isobaric and `W_3` if purely adiabatic. Then
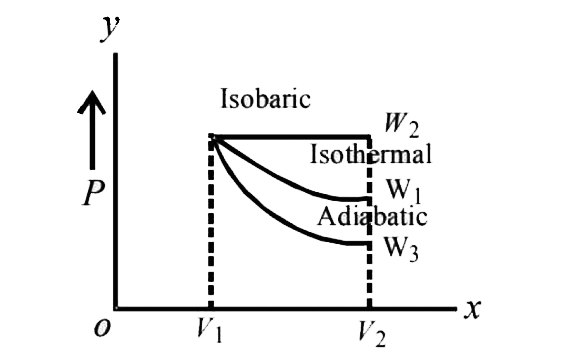
View SolutionP-V plots for two gases during adiabatic processes are shown in the figure. Plots 1 and 2 should corresponds respectively to

View SolutionThe work of 142kJ is performed in order to compress one kilo mole of gas adiabatically and in this process the temperature of the gas increases by `7^@C`. The gas is `(R=8.3Jmol^-1K^-1)`
View SolutionOne mole of an ideal gas at an initial temperature true of `TK` does `6R` joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is `5//3`, the final temperature of the gas will be
View SolutionIn the given (V-T) diagram, what is the relation between pressure `P_(1) and P_(2)` ?

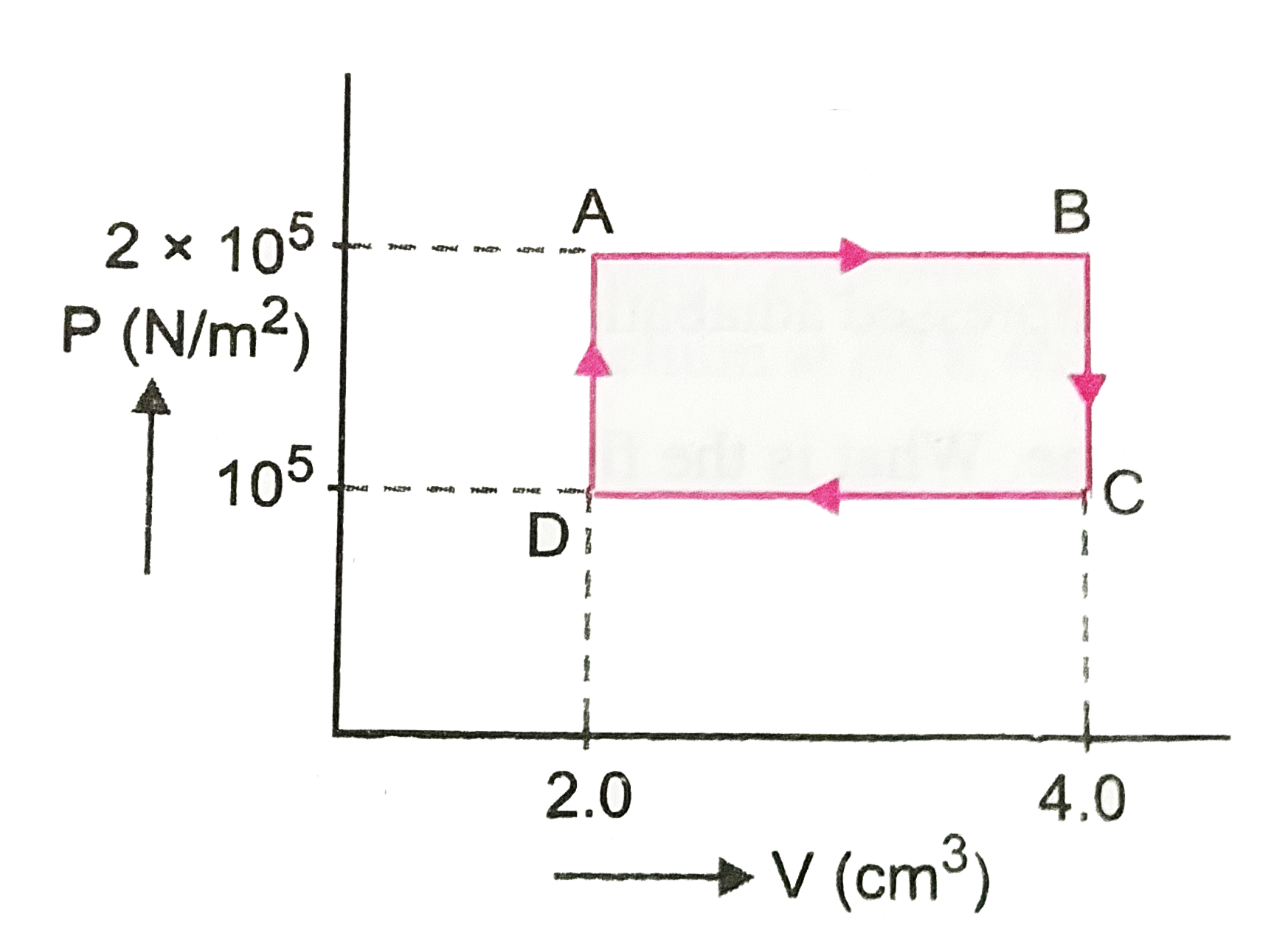
View SolutionThe `P-V` diagram of a gas undergoing a cyclic process ABCDA is shown in (figure). Where `P` is in `N//m^(2)` and `V` is in `cm^(3)`. Identify the incorrect statement
View SolutionTwo moles of helium gas are taken over the cycle ABCDA, as shown in the P-T diagram
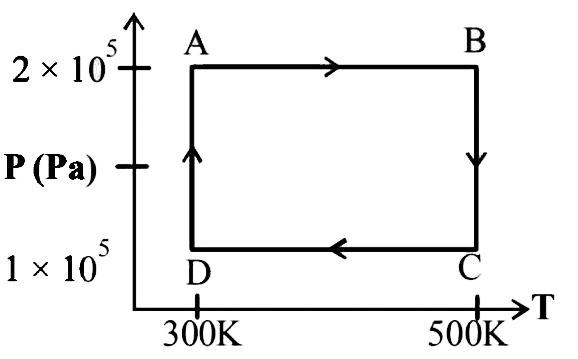
Assuming the gas to be ideal the work done on the gas in taking it form A to B is :
View SolutionTwo moles of helium gas are taken over the cycle ABCDA, as shown in the P-T diagram
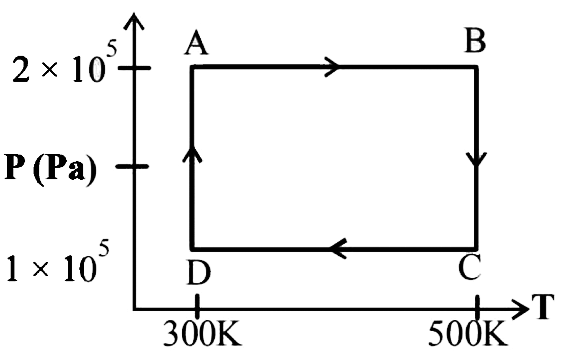
The work done on the gas in taking it from D to A is :
View SolutionTwo moles of helium gas are taken over the cycle ABCDA, as shown in the P-T diagram
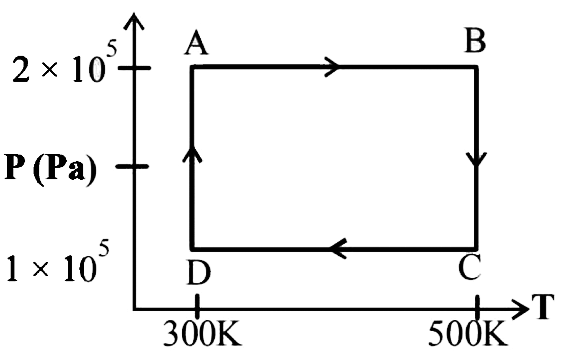
The net work done on the gas in the cycle ABCDA is :
View SolutionA monoatomic gas at pressure `P_(1)` and volume `V_(1)` is compressed adiabatically to `1/8th` of its original volume. What is the final pressure of gas.
View SolutionAn ideal gas is made go to through a cyclic thermodynamics process in four steps. The `Q_(2)= 300J, Q_(3)= - 400J, Q_(4)= -100J` respectively. The corresponding works involved are `W_(1)= 300J, W_(2)= -100J, W_(3)= 100J and W_(4)`. What is the value of `W_(4)`?
View SolutionA thermally insulated vessel contains an ideal gas of molecular mass M and ratio of specific heats `gamma`. It is moving with speed v and it's suddenly brought to rest. Assuming no heat is lost to the surroundings, Its temperature increases by:
View SolutionDuring an isothermal expansion, a confined ideal gas does `-150 J` of work aginst its surroundings. This implies that
View SolutionWhen `1 kg` of ice at `0^(@)C` melts to water at `0^(@)C`, the resulting change in its entropy, taking latent heat of ice to be `80 cal//g` is
View SolutionA mass of diatomic gas`(gamma=1.4)` at a pressure of 2 atomphere is compressed adiabitically so that its temperature rises from `27^(@)C` to `927^(@)C`. The pressure of the gas in the final state is
View Solution5.6 liter of helium gas at STP is adiabatically compressed to 0.7 liter. Taking the initial temperature to be `T_1,` the work done in the process is
View SolutionTwo moles of ideal helium gas are in a rubber balloon at `30^@C.` The balloon is fully expandable and can be assumed to require no energy in its expansion. The temperature of the gas in the balloon is slowly changed to `35^@C.` The amount of heat required in raising the temperature is nearly (take R
`=8.31 J//mol.K`)
View SolutionHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)

View SolutionOne mole of an ideal gas goes from an initial state A to final state B via two processs : It first undergoes isothermal expansion from volume `V` to `3 V` and then its volume is reduced from `3 V` to `V` at constant pressure. The correct `P-V` diagram representing the two process in (figure)
View SolutionAn ideal gas goes from State A to state B via three different process as indicate in the `P-V` diagram.
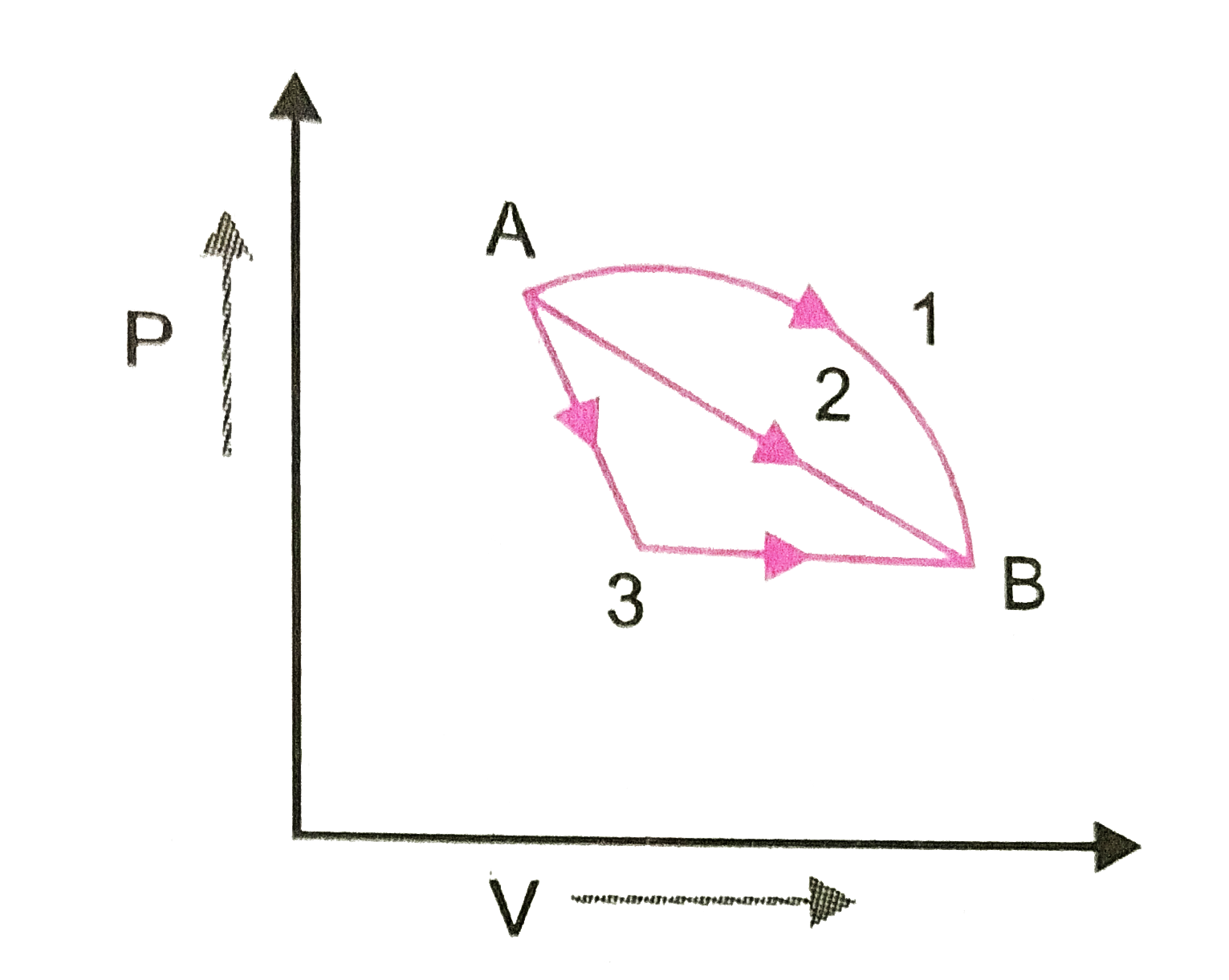
If `Q_(2), Q_(3)` indicates the heat absorbed by the gas along the three processes and `DeltaU_(1), DeltaU_(2), DeltaU_(3)` indicates the change in internal energy along the three processes respectively, then
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_P//C_V` for the gas is
View SolutionThe amount of heat energy required to raise the temperature of `1 g` of Helium at `NTP`, from `T_(1)K` to `T_(2)K` is
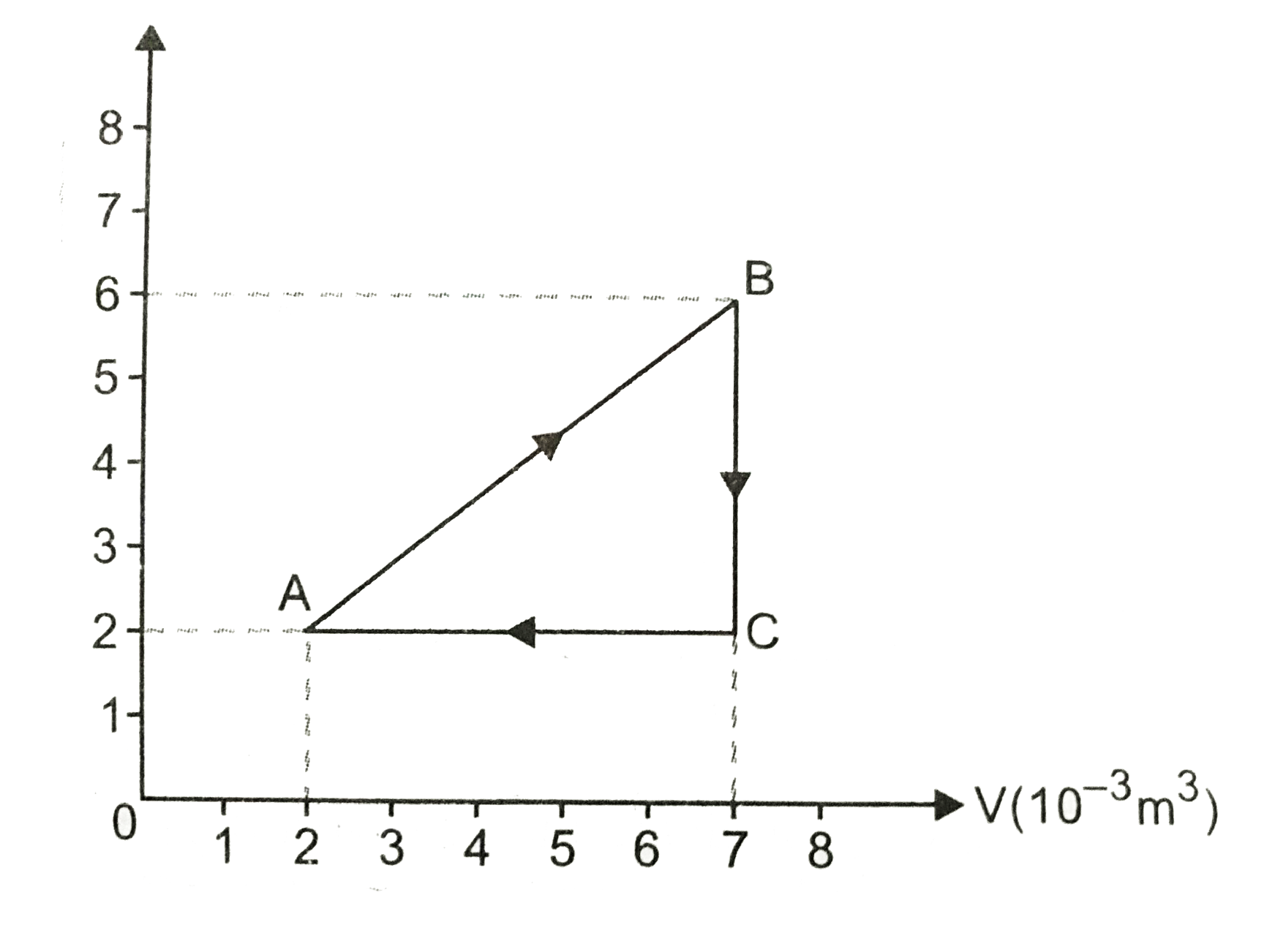
View SolutionA gas is taken through the cycle `A rarrB rarr C rarr A`, as shown in figure, what is the net work done by the gas?
View SolutionSteam at `100^(@)C` is passed into `20 g` of water at `10^(@)C` when water acquire a temperature of `80^(@)C`, the mass of water present will be
[Take specific heat of water `= 1 cal g^(-1).^(@) C^(-1)` and latent heat of steam ` = 540 cal g^(-1)`]
View SolutionA body at a temperature of `727^(@)C` and having surface area `5 cm^(2)`, radiations `300 J` of energy each minute. The emissivity is(Given Boltzmann constant `=5.67xx10^(-8) Wm^(-2)K^(-4)`
View SolutionA black body emit heat at the rate of `20 W`, when its tempertaure is `227^(@)C` Another black body emits heat at the rate of `15 W`, when its temperature is `227^(@)C`. Compare the area of the surface of the two bodies, if the surrounding is at `NTP`
View SolutionAccording to Wien's law
View SolutionOn observing light from three different stars `P`, `Q` and `R`, it was found that intensity of violet colour is maximum in the spectrum of `P`, the intensity of green colour is maximum in the spectrum of `R` and the intensity of red colour is maximum in the spectrum of `Q`. if `T_(P)`, `T_(Q)` and `T_(R)` are respective absolute temperature of `P`, `Q` and `R`. then it can be concluded from the above observation that
View SolutionIn (figure). shows two path that may be taken by a gas to go from a state A to state C
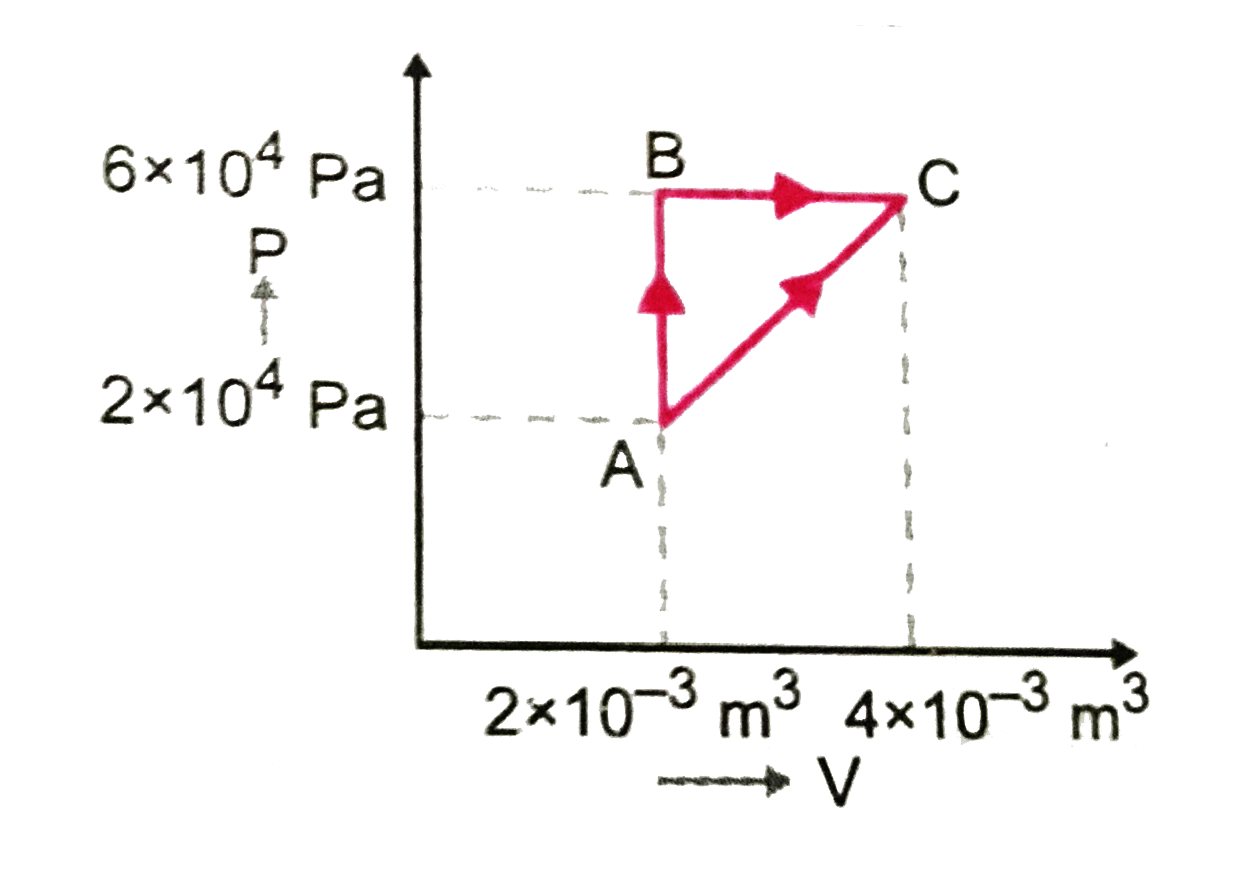
In the process AB, `400 J` of heat is added to the system and in process Bc, `100 J` of heat is added to the system. The heat absorbed by the system in the process AC will be
View SolutionThe two ends of a metal rod are maintained at temperature `100^(@)C` and `110^(@)C`. The rate of heat flow in the rod is found to be `4.0 J//s`. If the ends are maintained at temperature s `200^(@)C` and `210^(@)C`. The rate of heat flow will be
View SolutionAn ideal gas is compressed to half its initial volume by means of several peocesses. Which of the process results in the maximum work done on the gas ?
View SolutionThe value of coefficient of volume expansion of glycerin is `5 xx 10^(-4) K^(-1)`. The fractional change in the density of glycerin for a rise of `40^(@)C` in its temperature is
View SolutionThe balck body specturm of an object `O_(1)` is such that its radiant intensity (i.e., intensity per unit wavelength interval) is maximum at a wavelength of `200 nm`. Another object `Q_(2)` has the maximum radiant intensity at `600nm`. The ratio of power emitted per unit area by source `Q_(1)` to that of souce `O_(2)` is
View SolutionThree rods of Copper, Brass and Steel are welded together to from a Y shaped structure. Area of cross-section of each rod `=4cm^2`. End of copper rod is maintained at `100^@C` where as ends of brass and steel are kept at `0^@C`. Lengths of the copper, brass and steel rods are 46, 13 and 12 cm respectively. The rods are thermally insulated from surroundings excepts at ends. Thermal conductivities of copper, brass and steel are 0.92, 0.26 and 0.12 CGS units respectively. Rate of heat flow through copper rod is :
View SolutionA solid body of constant heat capacity `1J//^@C` is being heated by keeping it contact with reservoirs in two ways:
(i) Sequentially keeping in contact with 2 reservoirs such that each reservoir supplies same amount of heat.
(ii) Sequentially keeping in contact with 8 reservoir such that each reservoir supplies same amount of heat.
In both the cases body is brought from initial temperature `100^C` to final temperature `200^@C`. Entropy change of the body in the tow cases respectively is :
View SolutionA gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process untill its volume is again reduced to half. Then
View Solutionn' moles of an ideal gas undergoes a process `AtoB` as shown in the figure. The maximum temperature of the gas during the process will be:
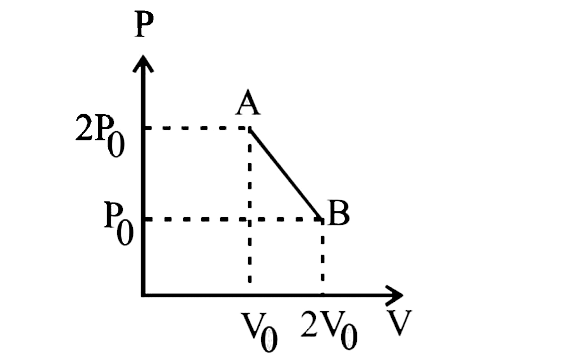
View SolutionIn a given process on an ideal gas, `dW=0 and dQlt0.` Then for the gas
View SolutionWhen a system is taken from state i to state f along the path iaf, it is found that `Q=50 cal and W=20 cal`. Along the path ibf `Q=36cal`. W along the path ibf is

View SolutionIn (figure). shows two path that may be taken by a gas to go from a state A to state C

In the process AB, `400 J` of heat is added to the system and in process Bc, `100 J` of heat is added to the system. The heat absorbed by the system in the process AC will be
View SolutionHow much heat energy should be added to a mixture of `10 g` of hydrogen and `40 g` of helium to change the temp. by `50^(@)C` kept in a closed vessel? Given `R= 2 cal//mol e K`
View SolutionIf `C_(p) and C_(v)` denote the specific heats (per unit mass of an ideal gas of molecular weight `M`), then
where `R` is the molar gas constant.
View SolutionAn ideal gas under goes a quasi static, reversible process in which its molar heat capacity C remains constant. If during this process the relation of pressure P and volume V is given by `PV^n=constant`, then n is given by (Here `C_P and C_V` are molar specific heat at constant pressure and constant volume, respectively):
View SolutionA Carnot engine, having an efficiency of `eta=1//10` as heat engine, is used as a refrigerator. If the work done on the system is 10J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionThe temperature `T_(1) and T_(2)` of heat reservoirs in the ideal carnot engine are `15000^(@)C` and `500^(@)C` respectivley. If `T_(1)` increases by `100^(@)C`, what will be the efficiency of the engine?
View SolutionA Carnot engine, having an efficiency of `eta=1//10` as heat engine, is used as a refrigerator. If the work done on the system is 10J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionCertain quantity of water cools from `70^(@)C` to `60^(@)C` in the first `5` minutes and to `54^(@)C` in the next `5` minutes. The temperature of the surrounding is
View SolutionThe cofficient of performance of a refrigerator is 5. If the temperature inside freezer is `-20^(@)C`, the temperature of the surroundings to which it rejects heat is :
View SolutionA refrigerator works between `4^(@)C` and `30^(@)C`. It is required to remove `600 calories` of heat every second in order to keep the temperature of the refrigerator space constant.The power required is (Take `1calorie= 4.2 J`)
View SolutionA carnot engine working between `300 K and 600 K` has work output of `800 J` per cycle. What is amount of heat energy supplied to the engine from source per cycle?
View SolutionA Carnot engine takes `3xx10^6cal`. of heat from a reservoir at `62^@C`, and gives it to a sink at `27^@C`. The work done by the engine is
View SolutionThe door of a running refrigerator inside a room is left open. The correct statement out of the following ones is
View SolutionA cannot engine has efficiency `(1)/(6)`. If temperature of sink is decreased by `62^(@)C` then its efficiency becomes `(1)/(3)` then the temperature of source and sink:
View SolutionAn ideal gas heat engine operates in Carnot cycle between `227^(@)C` and `127^(@)C`. It absorbs `6 x 10^(4) cals` of heat at higher temperature. Amount of heat converted to work is
View SolutionA Carnot engine whose sinl is at `300K` has an efficiency of `40%`. By how much should the temperature of source be increased so as to increase its efficiency by `50%` of original efficiency.
View SolutionA cannot engine has efficiency `(1)/(6)`. If temperature of sink is decreased by `62^(@)C` then its efficiency becomes `(1)/(3)` then the temperature of source and sink:
View SolutionA Carnot engine, having an efficiency of `eta=1//10` as heat engine, is used as a refrigerator. If the work done on the system is 10J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionA refrigerator with `COP= 1//3` release `200 J` at heat to a reservoir. Then the work done on the working substance is
View SolutionA Carnot engine operating between temperature `T_1 and T_2` has efficiency 1/6. When `T_2` is lowered by 62K its efficiency increase to 1/3. Then `T_1 and T_2` are, respectively:
View SolutionAn ideal gas heat engine operates in a Carnot cycle between `227^(@)C and 127^(@)C`. It absorbs `6K cal.` of heat at higher temperature. The amount of heat in `k cal` rejected to sink is
View SolutionA Carnot engine, whose efficiency is `40%`, takes in heat from a source maintained at a temperature of 500K. It is desired to have an engine of efficiency `60%`. Then, the intake temperature for the same exhaust (sink) temperature must be:
View Solution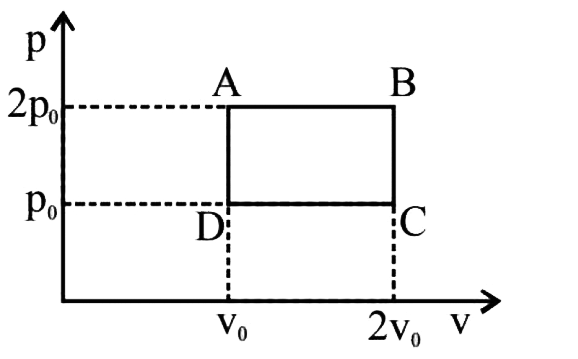
The above p-v diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas. The amount of heat, extracted from the source in a single cycle is
View SolutionIf a piece of metal is heated to temperature `theta` and the allowed to cool in a room which is at temperature `theta_0`, the graph between the temperature T of the metal and time t will be closet to
View SolutionThe work done in which of the following processes is zero
View SolutionIn which of the following process (es), there is no change in the internal energy of the system?
View SolutionIn a process on a system, the initial pressure and volume are equal to the final pressure and volume.
View SolutionThe pressure `p` and volume `V` of an ideal gas both increase in a process.
View SolutionLet `Q and W` denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
View SolutionA gas kept in a container of finite conductivity is suddenly compressed . The process
View SolutionRefer to figure `DeltaU_(1)` and `DeltaU_(2)` be the changes in internal energy in the system in process `A+B` and `DeltaW` be the net work done by the system in the process `A+B`,

View SolutionOne mole of an ideal gas in initial state A undergoes a cyclic process ABCA, as shown in the figure. Its pressure at A is `P_0`. Choose the correct option (s) from the following
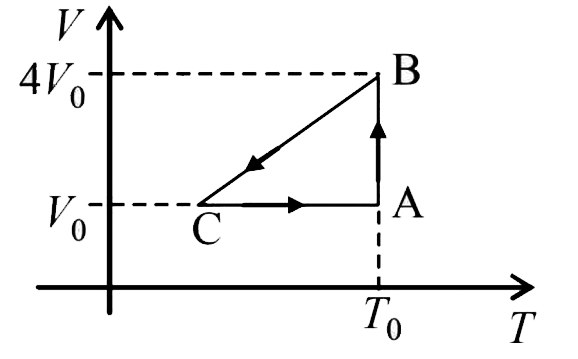
View SolutionA system goes from A and B via two processes. I and II as shown in figure. If `DeltaU_1 and DeltaU_2` are the changes in internal energies in the processes I and II respectively, then
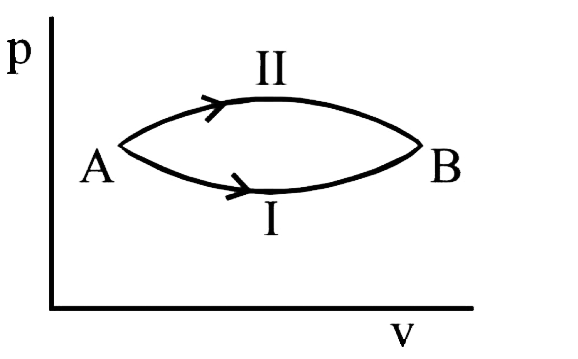
View SolutionThe temperature -entropy diagram of a reversible engine cycle is given in the figure. Its efficiency is
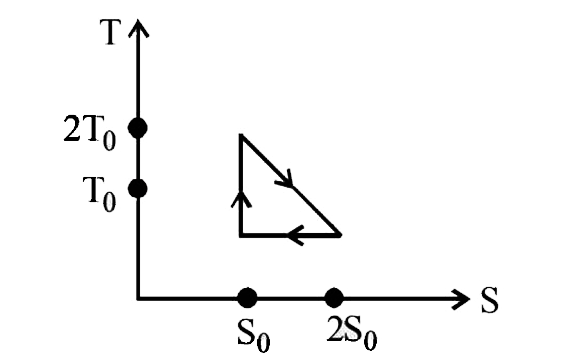
View SolutionThe internal enegy of an ideal gas decreases by the same amount as the work done by the system.
View SolutionWhich of the following graphs correctly represents the variation of `beta=-(dV//dP)/V`
with P for an ideal gas at constant temperature?
View SolutionA gas is copmressed isothermally to half its volume. BY what factor does the pressure of the gas increase ? Given `gamma=1.4`
View SolutionA gas is compressed adiabatically to half its volume. By what factor does the pressure of the gas increase?
View SolutionA gas is suddenly compressed to `1/4th` of its original volume. Caculate the rise in temperature when original temperature is `27^(@)C. gamma= 1.5`.
View SolutionA Carnot engine absorbs `6xx10^(5)cal`. At `227^(@)C`. Heat rejected to the sink at `127^(@)C` is
View SolutionWork done //cycle by the engine in the above questions is
View SolutionEfficiency of the engine in the above questions is
View SolutionAt what temperature should the sink be maintained to increase the efficiency by `10%`?
View SolutionWhat should be the temperature of the source to increases the efficiency to `30%`
View Solution
Multiple choice questions. questions and complete solutions for chapter THERMODYNAMICS of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS THERMODYNAMICS
- Advanced problems for competitions
- Assertion- Reason Type Questions
- Conceptual Problems
- Curiosity Question
- Higher order thinking skills
- Interger Type questions
- Long answer questions
- Long answer questions(NCERT)
- Multiple choice questions
- Multiple choice questions (NCERT)
- Multiple choice questions.
- NCERT Questions
- Problems for practice
- Sample problems
- Short answer questions
- Short answer questions(NCERT)
- Solved examples
- Value based Questions
- Very short answer questions
- Very short answer questions(NCERT)