Complete Solutions to Multiple choice questions-I of chapter BEHAVIOUR OF PERFECT GAS & KINETIC THEORY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | BEHAVIOUR OF PERFECT GAS & KINETIC THEORY |
| PRADEEP | Multiple choice questions-I |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
A cubic vessel (with face horizontal + vetical ) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of `500 ms^(-1)` in vertical direction. The pressure of the gas inside the vessel as observed by us on the ground.
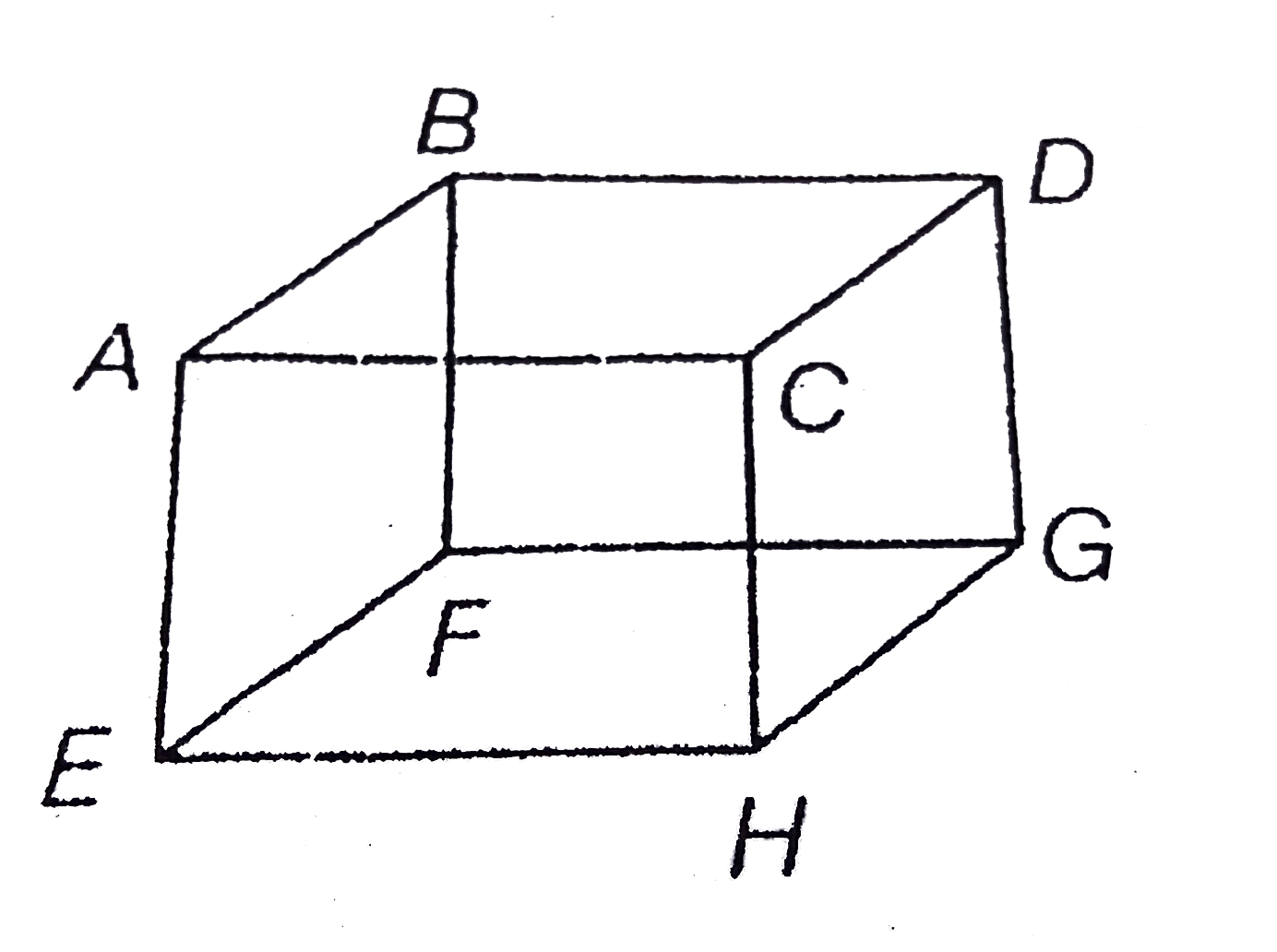
View SolutionMole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it .At any given time.
View SolutionBoyle's law is applicable for an
View SolutionA cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (figure). If the temperature is increased

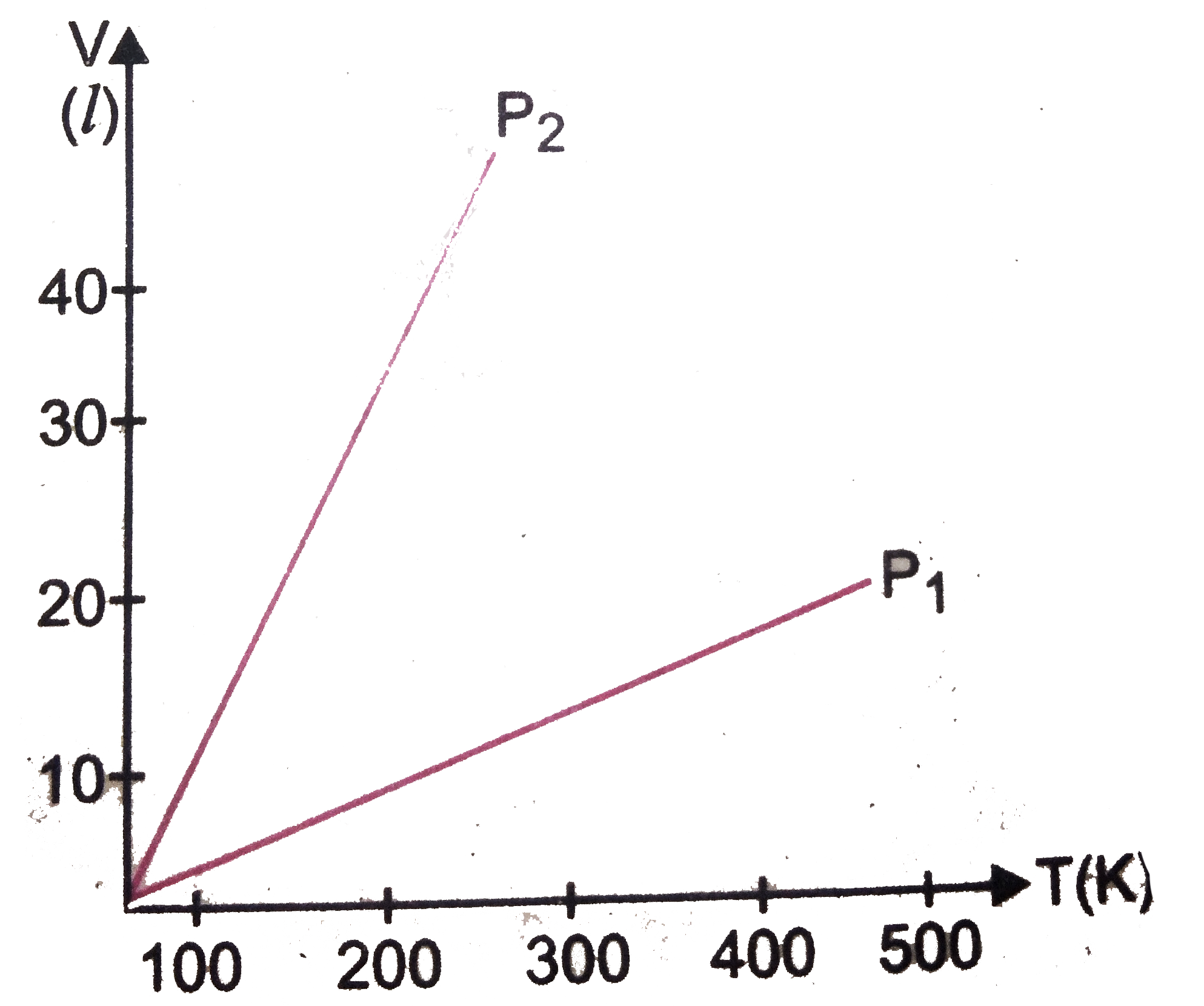
View SolutionVolume versus temperature graphs for a given mass of an ideal gas are shown in Fig. at two different values of constant pressure. What can be inferred about relation between `P_(1) and P_(2)`?
View Solution1 mole of `H_(2)` gas is contained in box of volume `V= 1.00 m^(3) at T = 300 K`. The gas is heated to a temperature of T = 3000 K and the gas gets converted to a gas of hydrogen atoms. The final pressure would be (considering all gases to be ideal)
View SolutionA vessel of volume V contains a mixture of 1 mole of hydrogen and 1 mole oxygen (both considered as ideal). Let `f_(1)(v) dv,` denote the fraction of molecules with speed between v and (v+ dv) with `f_(2)(v)dv`, similarly for oxygen . Then ,
View SolutionAn inflated rubber balloon contains one mole of an ideal gas has a pressure p, volume V and temperature T. if the temperature rises to 1.1 T, and the volume is increased to 1.05 V, the final pressure will be
View SolutionDiatomic molecules like hydrogen haven energy due to both translational as well as rotational motion. From the equation in kinetic theory `PV=(2)/(3)E,E` is
View SolutionIn a diatomic molecule, the rotational energy at given temperature
View SolutionWhich of the following diagrams, Fig. depicts ideal gas behaviour ?
View SolutionWhen an ideal gas is compressed adiabatically, is temperature rises the molecule have more kinetic energy than before. The kinetic energy increases,
View SolutionA gas at 300 K has pressure `4 xx 10^(-10) N//m^(2)`. IF `k = 1.38 xx 10^(-23) J//K`, the number of `"molecule"// cm^(3)` is of the order of
View Solution16 gram of oxygen, 14 gram of nitrogen and 11 gram of carbon dioxide are mixed in an enclosure of volume 5 L and temperature `27^(@)C. The pressure exerted by the mixture is
View SolutionA gas is found to obey the law `P^(2)V = constant`. The initial temperature and volume are `T_(0) and V_(0)`. If the gas expands to a volume `3 V_(0)`, its final temperature becomes
View SolutionThe specific heat of the mixture of two gases at constant volume is `(13)/(6) R`. The ratio of the number of moles of the first gas to the second gas is 1:2.
The respective gases may be
View SolutionThe equation of state for 5 g of oxygen at a pressure P and temperature T, when occupying a volume V, will be
View SolutionA certain amount of gas is sealed in a glass flask at 1 atmosphere pressure and `20^(@)C`. The flask can withstand upto a pressure of 2 atmosphere. Find the temperature to which gas can be heated so that the flask does not break.
View SolutionThe temperature of an open room of volume `30 m^(3)` increases from `17^(@)C to 27^(@)C` due to sunshine. The atmospheric pressure in the room remains `1 xx 10^(5) Pa`. If `n_(i) and n_(f)` are the number of molecules in the room before and after heating then `n_(f)` and `n_(i)` will be
View SolutionWhen a gas filled in a closed vessel is heated through `1^(@)C`, its pressure increases by 0.4%. What is the initial temperature of gas ?
View SolutionTemperature ramaining constant, the pressure of gas is decreased by 20%. The percentage change in volume is
View SolutionAt `10^(@)C`, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at `110^(@)C`, this ratio is
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume `V_1` and contains ideal gas at pressure `P_1` and temperature `T_1`.The other chamber has volume `V_2` and contains ideal gas at pressure `P_2` and temperature `T_2`. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionOne litre of oxygen at a pressure of 1 atm and two litres of nitrogen at a pressure of 0.5 atm are introduced into a vessel of volume 1 litre. If there is no change in temperature, the final pressure of the mixture of gas (in atm) is
View SolutionA container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
View SolutionIf gas molecules undergo inelastic collision with the walls of container when temperature of gas is same as that of walls of container, then
(a) the temperature of the gas will decrease
the pressure of the gas will increase
( c) neither the temperature nor the pressure will change.
(d) the temperature of the gas will increase
View SolutionIn the given (V-T) diagram, what is the relation between pressure `P_(1) and P_(2)` ?

View SolutionAn open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)
View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature `T_1`, pressure `P_1` and volume `V_1`and the spring is in its relaxed state. The gas is then heated very slowly to temperature `T_2`,pressure `P_2`and volume `V_2`. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)

View SolutionThe rms speed of oxygen molecules at a certain temperature is `upsilon`. If the temperature is doubled and the oxygen gas dissociates into atomic oxygen, the rms speed would be
View SolutionConsider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increase as `V^q`, where V is the volume of the gas. The value of q is : `(gamma=(C_p)/(C_v))`
View SolutionA gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
View SolutionThe ratio of the specific heats `(C_(P))/(C_(upsilon)) = gamma` in terms of degrees of freedom is given by
View SolutionThe molar specific heat of a gas as given from the kinetic theory is `(5)/(2) R`. If it is not specified whether it is `C_(p) or C_(upsilon)` one could conclude that the molecules of the gas
View SolutionTwo vessel separately contains two ideal gases A and B at the same temperature, the pressure of A being twice that of B. under such conditions, the density of A is found to be 1.5 times the density of B. the ratio of molecular weight of A and B is
View SolutionA gas is filled in a container at pressure `P_(0)`. If the mass of molecules is halved and their rms speed is doubled, then the resultant pressure would be
View SolutionIn a mixture of gases, the average number of degrees of freedom per molecule is 6. the rms speed of the molecules of the gas is C. the velocity of sound in the gas is
View SolutionThree moles of oxygen ar mixed with two moles of helium. What will be the ratio of specific heats at constant pressure and constant volume for the mixture ?
View SolutionFour cylinders contain equal number of moles of argon, hydrogen, nitrogen and carbon dioxide at the same temperature. The energy is minimum in
View SolutionOxygen and hydrogen gas are at same temperature and pressure. And the oxygen molecule has 16 times the mass of hydrogen molecule. Then the ratio of their rms speed is
View SolutionThe average translational energy and the rms speed of molecules in a sample of oxygen gas at `300K` are `6.21xx10^(-21)J` and `484m//s`, respectively. The corresponding values at `600K` are nearly (assuming ideal gas behaviour)
View SolutionThe K.E. of one mole of an ideal gas is
View SolutionAt what temperature is the rms velocity of a hydrogen molecule equal to that of an oxygen molecule at `47^(@)C`?
View SolutionThe molar specific heat at constant pressure of an ideal gas is `(7//2 R)`. The ratio of specific heat at constant pressure to that at constant volume is
View SolutionTwo rigid boxes containing different ideal gases are placed on a table. Box A contains one mole of nitrogen at temperature `T_0`, while Box contains one mole of helium at temperature `(7/3)T_0`. The boxes are then put into thermal contact with each other, and heat flows between them until the gasses reach a common final temperature (ignore the heat capacity of boxes). Then, the final temperature of the gasses, `T_f` in terms of `T_0` is
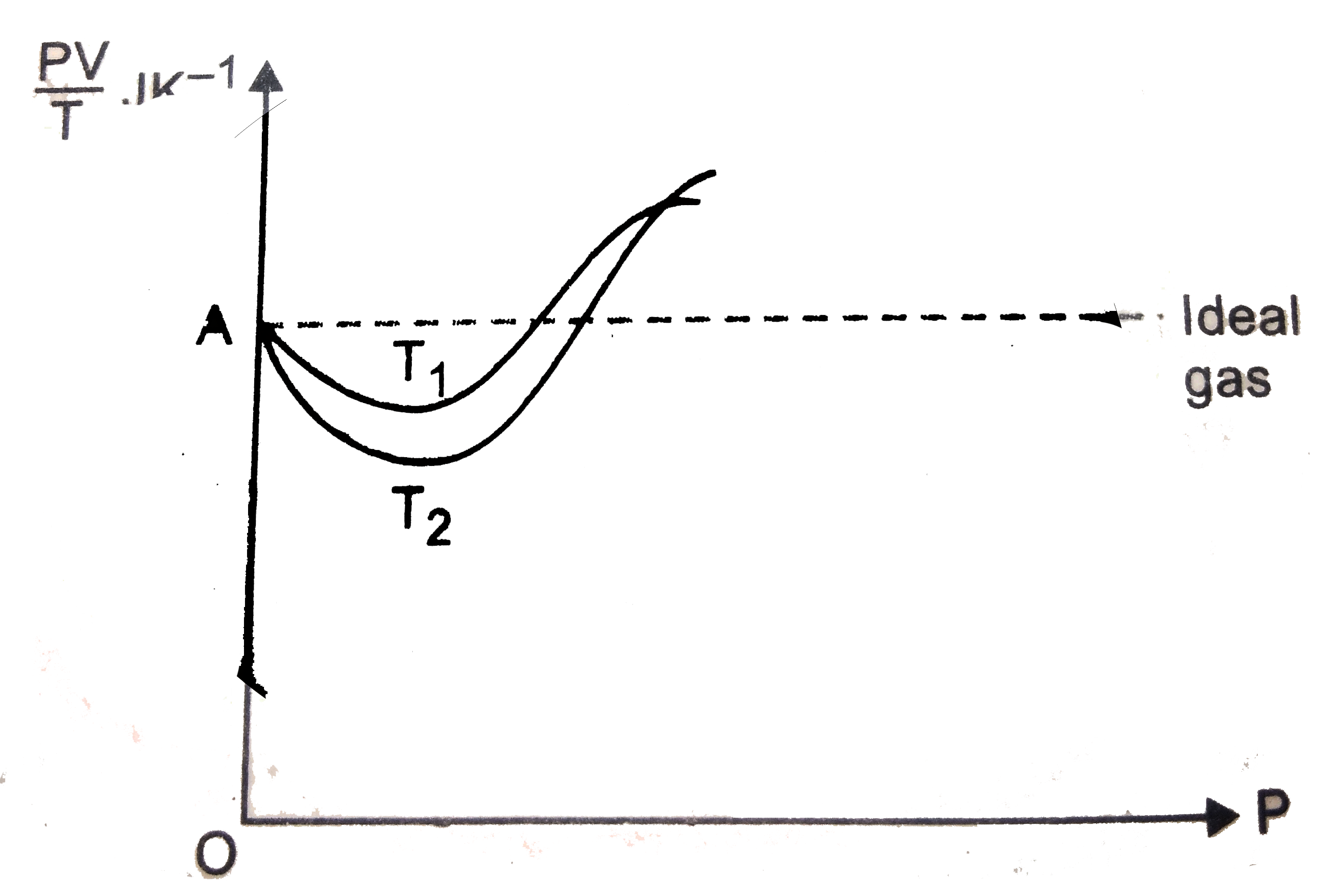
View SolutionGiven is the graph between `(PV)/T` and P for 1 gm of oxygen gas at two different temperatures `T_(1) and T_(2)` Fig. Given, density of oxygen `= 1.427 kg m^(-3)`. The value of `(PV)//(T)` at the point A and the relation between `T_(1) and T_(2)` are respectively :
View SolutionThe root mean square velocity of hydrogen molecules at 300 K is `1930 ms^(-1)`. The rms velocity of oxygen molecules at 1200 K will be
View SolutionTwo moles of oxygen are mixed with eight moles of helium. The effective specific heat of the mixture at constant volume is
View Solution1 mole of monoatomic and one mole of diatomic gas are mixed together. The value of `C_(upsilon)` is
View SolutionOne kg of a diatomic gas is at pressure of `8xx10^4N//m^2`. The density of the gas is `4kg//m^3`. What is the energy of the gas due to its thermal motion?
View Solution10 moles of an ideal monoatomic gas at `10^(@)C` are mixed with 20 moles of another monoatomic gas at `20^(@)C`. Then the temp. of the mixture is
View SolutionFind the temperature at which oxygen molecules would have the same rms speed as of hydrogen molecules at `300 K`.
View SolutionMean free path of a gas molecule is
View SolutionA mixture of 2 moles of helium gas (`(atomic mass)=4a.m.u`) and 1 mole of argon gas (`(atomic mass)=40a.m.u`) is kept at 300K in a container. The ratio of the rms speeds `((v_(rms)(helium))/((v_(rms)(argon))` is
View SolutionThe molar specific heats of an ideal gas at constant pressure and volume are denotes by `C_(P)` and `C_(upsilon)` respectively. If `gamma = (C_(P))/(C_(upsilon))` and `R` is the universal gas constant, then `C_(upsilon)` is equal to
View SolutionThe mean free path of molecules of a gas (radius r) is inversely proportional to
View SolutionThe root mean square velocity of hydrogen molecule at `27^(@)C is (upsilon_(H)` and that of oxygen at `402^(@)C is (upsilon_(0)`, then
View SolutionThe molecules of a given mass of a gas have rms velocity of `200 m//s at 27^(@)C and 1.0 xx 10^(5) N//m_(2)` pressure. When the temperature and pressure of the gas are respectively `127^(@)C and 0.05 xx 10^(5) Nm^(-2)`, the rms velocity of its molecules in `ms^(-1)` is
View SolutionA gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
View Solution
Multiple choice questions-I questions and complete solutions for chapter BEHAVIOUR OF PERFECT GAS & KINETIC THEORY of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- Advance problem for competitions
- Assertion - Reason Type questions
- Conceptual Problems
- Curiosity Question
- Fill in the blanks
- Higher order thinking skills questions
- Integer type questions
- Long answer questions
- Multiple choice questions-I
- Multiple choice questions-II
- Multiple choice questions-III
- NCERT questions
- Problems for practice
- Sample problem
- Short answer questions
- Solved Examples
- Value Based Questions
- Very short Answer questions